選考チューニングのRLHFを数式ベースで理解する（報酬モデリング編）

大規模言語モデル入門および大規模言語モデル入門II出てくるRLHFについて、少し数式で詰まった部分があったので、メモがてら数式の意味を記載していこうと思います。
章番号や数式の番号は書籍のものなので、下記書籍を持ってないとなんのこっちゃだと思います。

https://gihyo.jp/book/2023/978-4-297-13633-8

https://gihyo.jp/book/2024/978-4-297-14393-0

対象は、4.5.1項および12.1.1項です。

報酬モデリングの数式

eq(12.1)

下記の式変形です。

$$\frac{\exp(r^*(x, y^1))}{\exp(r^*(x, y^1)) + \exp(r^*(x, y^2))} = \sigma(r^*(x, y^1) - r^*(x, y^2))$$

シグモイド関数は、下記となるので、この形を目指していきます。

$$\frac{1}{1 + \exp(-x)}$$

（手書きですみません）

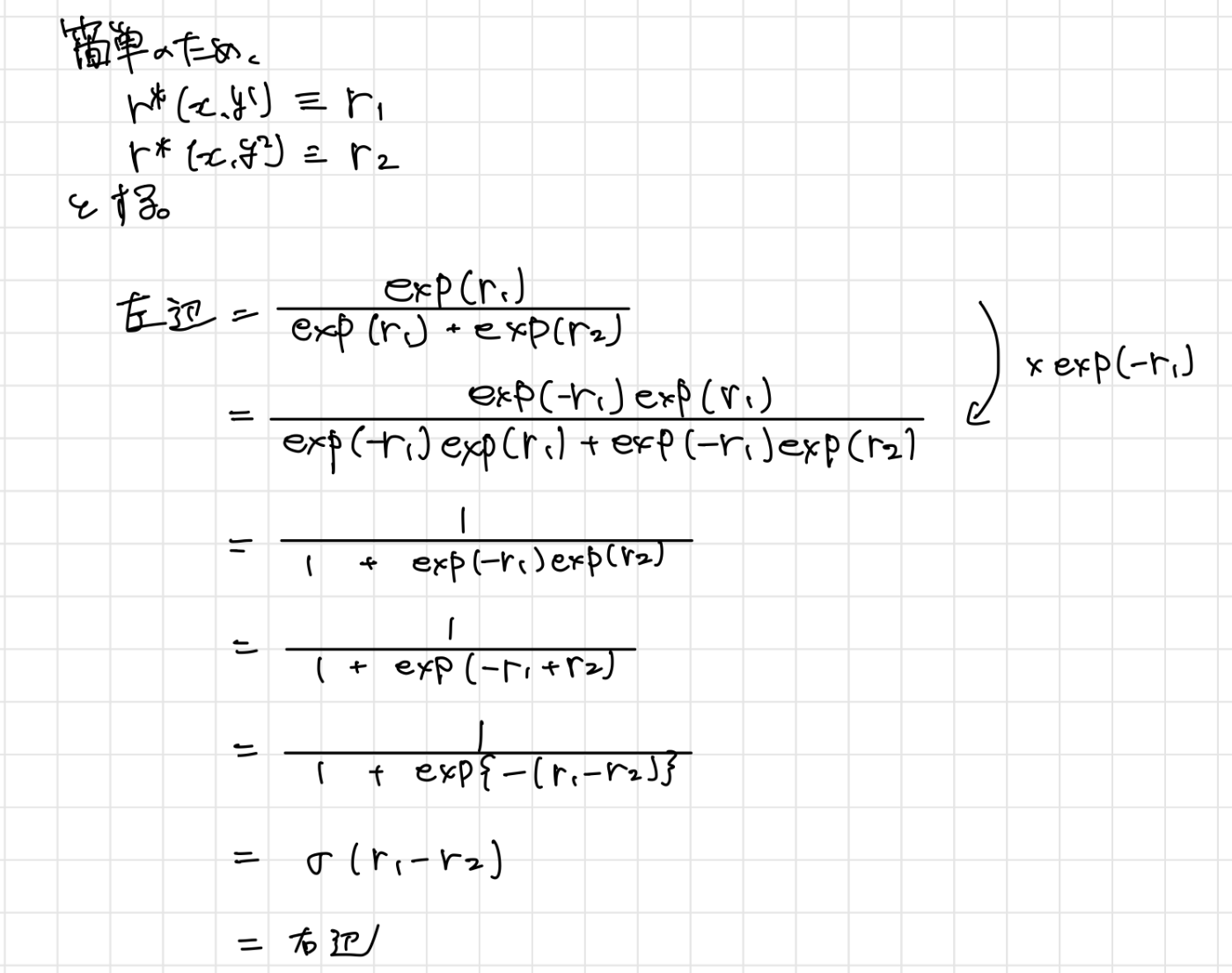
eq(4.2)およびeq(12.2)

多少の表記ゆれ（定義の違い）があるだけで同じものなので、eq(12.2)ベースでみていきます。

下記損失関数(12.2)を最小化するように学習させます。

$$\mathcal{L}(\theta) = -\mathbb{E}_{(x,y^+,y^-) \sim D_{\text{p}}} \left[ \log \left( \sigma \left( r_\theta(x, y^+) - r_\theta(x, y^-) \right) \right) \right]$$

ここで、$\mathbb{E[\cdot]}$は期待値、$D_{\text{p}}$はデータセット、$x, y^+, y^-$はデータセット$D_{\text{p}}$から抽出されたプロンプトと好ましい応答と好ましくない応答、$r_\theta(x, y^+)$は好ましい応答に対する報酬モデルの出力、$r_\theta(x, y^-)$は好ましくない応答に対する報酬モデルの出力、$\sigma(\cdot)$はシグモイド関数です。

では、一つ一つ、どんな式なのか理解していきましょう。

$$r_\theta(x, y^+) - r_\theta(x, y^-)$$

こちらは簡単ですね。好ましい応答に対する報酬と好ましい応答に対する報酬の差です。
好ましい応答尾の報酬を大きくしたいため、$r_\theta(x, y^+) - r_\theta(x, y^-)$が正になってほしい、というお気持ちはわかると思います。
これにシグモイド関数を適用するとどうなるでしょう。

• $r_\theta(x, y^+) - r_\theta(x, y^-)$が0より大きくなると、$\sigma(\cdot)$は1に近づく（こちらになることを期待している）
• $r_\theta(x, y^+) - r_\theta(x, y^-)$が0より小さくなるとなると、$\sigma(\cdot)$は0に近づく

さらに、これに$\log$を適用しているので

• $r_\theta(x, y^+) - r_\theta(x, y^-)$が0より大きくなると、$\log \left( \sigma(\cdot) \right)$は0に近づく
• $r_\theta(x, y^+) - r_\theta(x, y^-)$が0より小さくなると、$\log \left( \sigma(\cdot) \right)$は$-\infty$に近づく

となります。
$\log \left( \sigma \left( r_\theta(x, y^+) - r_\theta(x, y^-) \right) \right)$の期待値のマイナスをかけたものを最小化したい。
つまり、$r_\theta(x, y^+) - r_\theta(x, y^-)$が大きい正の数になるように学習させたいことがわかると思います。

このようにしてチューニングされた報酬モデル$r_\theta$を用いて、LLMが出力する文章に対して報酬$r_\theta(x, y)$を返していきます。