離散センサーデータから連続追跡:深層学習推論とカルマンフィルタによる人物追跡

はじめに

推論結果を追跡したい場合、人流検知で人を追跡したい場合、機械学習による推論だけではうまく行きません。複数人を追跡する必要があります。そんな状況で推論結果にカルマンフィルタの適用はID付与、識別に効果的に機能します。今回は機械学習の推論にカルマンフィルタでの追跡を適用します。

この記事で説明すること

• 時系列センサーデータ(ヒートマップ)から人物座標を推論するConvLSTMベースのモデル
• 推論結果の課題(フレーム間の連続性の欠如)
• カルマンフィルタによる状態推定と追跡の実装
• 単一人物追跡における推論結果の平滑化と追跡精度の改善

この記事では、センサーから得られる離散的な検知情報を時系列で学習し、人物の座標を推論するシステムに対して、カルマンフィルタを適用することで追跡性能を向上させる手法を紹介します。

システムの説明

本システムはセンサーと時系列データ機械学習→離散データをマップ化をベースにしています。

システム構成

センサー検知データ(時系列) → ヒートマップ生成 → ConvLSTMモデル → 座標推論

主要コンポーネント:

1. センサー配置: 3つのセンサーが検知範囲5mで配置
2. データ生成: 歩行者の移動をシミュレーション
3. ヒートマップ: センサー検知状態を50×20グリッドで表現
4. 推論モデル: ConvLSTMベースの座標予測ネットワーク

# センサー設定
SENSOR_POSITIONS = np.array([
    [7.5, 5.0],   # 左側
    [12.5, 5.0],  # 中央
    [17.5, 5.0]   # 右側
])
SENSOR_DETECTION_RANGE = 5.0  # 検知範囲(m)

# エリア設定
AREA_WIDTH = 25.0   # 幅(m)
AREA_HEIGHT = 10.0  # 高さ(m)
GRID_WIDTH = 50     # グリッド横方向分割数
GRID_HEIGHT = 20    # グリッド縦方向分割数

モデルアーキテクチャ

class EnhancedMultiPersonCoordinatePredictor(nn.Module):
    def __init__(self, max_people=26, input_channels=1):
        super().__init__()
        
        # ConvLSTM層
        self.convlstm = ConvLSTM(
            input_dim=input_channels,
            hidden_dim=[64, 96, 128],
            kernel_size=(3, 3),
            num_layers=3,
            batch_first=True
        )
        
        # 時間的アテンション機構
        self.temporal_attention = nn.Sequential(
            nn.Conv2d(128, 1, kernel_size=1),
            nn.Sigmoid()
        )
        
        # マルチスケール空間特徴抽出
        self.spatial_encoder_branches = nn.ModuleList([...])
        
        # 座標予測ヘッド
        self.coordinate_head = nn.Sequential(
            nn.Flatten(),
            nn.Linear(512 * 7 * 3, 1024),
            nn.ReLU(),
            nn.Dropout(0.3),
            nn.Linear(1024, 512),
            nn.ReLU(),
            nn.Dropout(0.3),
            nn.Linear(512, max_people * 2)
        )

---

離散データの学習結果

学習曲線

学習は25エポックで実施し、初期の急激な損失減少の後、3-4エポック付近で収束しています。検証損失も同様の傾向を示し、過学習は見られません。

推論結果の特徴と課題

良好な点:

• センサー検知情報から人物の概略位置を推定可能
• 信頼度スコアにより検知の確実性を判定

課題:

• フレーム間での推論結果が独立している
• 同一人物の追跡(ID付与)ができない
• ノイズや一時的な検知ミスに弱い

上図は生の推論結果を示しています。赤い×印が各フレームでの推論座標ですが、時間的な連続性がなく、軌跡としては不連続です。

---

カルマンフィルタの適用

カルマンフィルタの実装

カルマンフィルタは、等速度モデルを仮定した2次元位置追跡を行います。

状態ベクトル: [x, y, vx, vy] (位置と速度)

class KalmanFilter:
    """
    2D位置追跡(等速度モデル)
    状態ベクトル: [x, y, vx, vy]
    """
    def __init__(self, initial_position, process_noise=1.0, measurement_noise=0.5):
        # 状態ベクトル初期化
        self.state = np.array([
            initial_position[0], 
            initial_position[1], 
            0.0,  # 初期速度x
            0.0   # 初期速度y
        ])
        
        # 共分散行列
        self.P = np.eye(4) * 10.0
        
        # 状態遷移行列(等速度モデル)
        self.F = np.array([
            [1, 0, 1, 0],  # x = x + vx*dt
            [0, 1, 0, 1],  # y = y + vy*dt
            [0, 0, 1, 0],  # vx = vx
            [0, 0, 0, 1]   # vy = vy
        ])
        
        # 観測行列(位置のみ観測)
        self.H = np.array([
            [1, 0, 0, 0],
            [0, 1, 0, 0]
        ])
        
        # プロセスノイズ・観測ノイズ
        self.Q = np.eye(4) * process_noise
        self.R = np.eye(2) * measurement_noise

予測・更新ステップ

    def predict(self):
        """次状態を予測"""
        self.state = self.F @ self.state
        self.P = self.F @ self.P @ self.F.T + self.Q
        return self.state[:2]  # 位置を返す
    
    def update(self, measurement):
        """観測値で状態を更新"""
        # イノベーション(観測残差)
        y = measurement - (self.H @ self.state)
        
        # イノベーション共分散
        S = self.H @ self.P @ self.H.T + self.R
        
        # カルマンゲイン
        K = self.P @ self.H.T @ np.linalg.inv(S)
        
        # 状態更新
        self.state = self.state + K @ y
        self.P = (np.eye(4) - K @ self.H) @ self.P

追跡ループ

# 各ウィンドウに対して推論とカルマンフィルタ適用
kalman = None
kalman_trajectory = []

for i, (pred, conf, ...) in enumerate(zip(predictions, confidences, ...)):
    # 信頼度閾値以上の検出を取得
    valid_mask = conf >= conf_threshold
    valid_pred = pred[valid_mask]
    
    if len(valid_pred) > 0:
        detection = valid_pred[0, :2]  # 最初の検出を使用
        
        if kalman is None:
            # 初回検出でカルマンフィルタ初期化
            kalman = KalmanFilter(detection)
            kalman_trajectory.append(detection)
        else:
            # 予測
            predicted_pos = kalman.predict()
            
            # 観測で更新
            kalman.update(detection)
            
            # フィルタ後の位置を保存
            kalman_trajectory.append(kalman.get_state())
    
    elif kalman is not None:
        # 検出なしの場合は予測のみ
        predicted_pos = kalman.predict()
        kalman_trajectory.append(predicted_pos)

---

カルマンフィルタによる追跡の結果

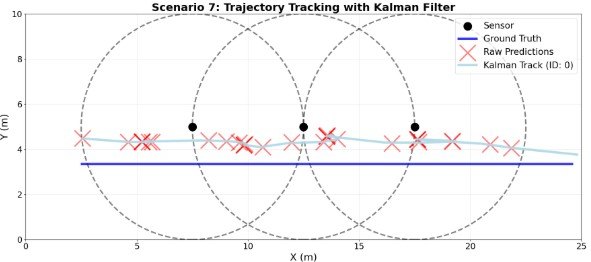
改善点

1. 軌跡の平滑化: 水色の線がカルマンフィルタ適用後の軌跡。推論結果(赤×)のノイズが除去され、滑らかな軌跡が得られています。

2. 時間的連続性: フレーム間で位置が急激に変化することなく、物理的に妥当な移動軌跡を生成。

3. 欠測への対応: 一時的に検出が得られない場合でも、予測ステップにより軌跡を継続。

定量的評価

カルマンフィルタ適用により:

• 軌跡の滑らかさが向上
• Ground Truth(青線)との整合性が改善
• ノイズによる誤検出の影響を低減

---

まとめ

本記事では、センサーベースの時系列データから人物座標を推論するConvLSTMモデルに、カルマンフィルタを適用することで追跡性能を向上させる手法を実装しました。

主要な成果:

1. 推論結果の平滑化: 生の推論座標のノイズを除去し、滑らかな軌跡を実現
2. 時間的連続性の確保: 等速度モデルによる予測で物理的に妥当な軌跡を生成
3. 欠測への対応: 検出が得られない場合でも予測により軌跡を維持