【図解】完全関数従属・部分関数従属
はじめに
この記事は以下の記事の続きとして書いています。
以下の前提の記事になります。
- 第1正規化の知識がある
- 候補キー・非キー属性の定義と特定方法がわかる
もし自信が無ければ、上記の記事を先に読んでもらえれば幸いです!
第2正規形の条件の確認
「テーブルのいずれの候補キーに対しても、非キー属性が部分関数従属していない。」
これが、第2正規形の条件になります。
候補キー・非キー属性については前の記事で説明していますので、この記事では関数従属について深堀りしていきます。
関数従属(Functional Dependency:FD)とは
「X が決まれば Y が決まる」 という関係性を 関数従属性(Functional Dependency:FD) があるといいます。
この関数従属という単語はデータベースに限らず数学でも使われます。
データベースに当てはめて考えると列の依存関係というとわかりやすいかと思います。
「受注番号(X) が決まれば 顧客コード(Y) が決まる」のような関係ですね

特に第2正規形を理解するためには関数従属の中でも
- 完全関数従属(Full Functional Dependency:FFD)
- 部分関数従属(Partial Functional Dependency:PFD)
の2つを理解する必要があります。これからこれらを説明していきます。
完全関数従属(Full Functional Dependency:FFD)の例
非キー属性が候補キーに対し完全関数従属している例を説明していきます。
候補キーが1列(1属性)の例
- 候補キー: 商品コード
- 非キー属性: 単価
- FD: 商品コード → 単価

候補キーの 商品コード が決まれば非キー属性の 単価 が決まります。
このとき
「非キー属性(単価)は候補キー(商品コード)に完全関数従属している」
といいます。
候補キーが2列(2属性)の場合
- 候補キー: 商品コード+受注番号
- 非キー属性: 受注数
- FD:(商品コード+受注番号) → 受注数

候補キー(商品コード+受注番号)の列全てが決まると非キー属性(受注数)が決まるので
「 非キー属性(受注数)は候補キー(商品コード+受注番号)に完全関数従属している」
といえます。この商品コード+受注番号両方必要というところが大事なポイントです!
候補キーが複数ある場合
- 候補キー1: 商品コード+受注番号
- 候補キー2: 行ID
- 非キー属性: 受注数
- FD: (商品コード+受注番号) → 受注数、行ID
- FD: 行ID → 商品コード、受注番号、受注数
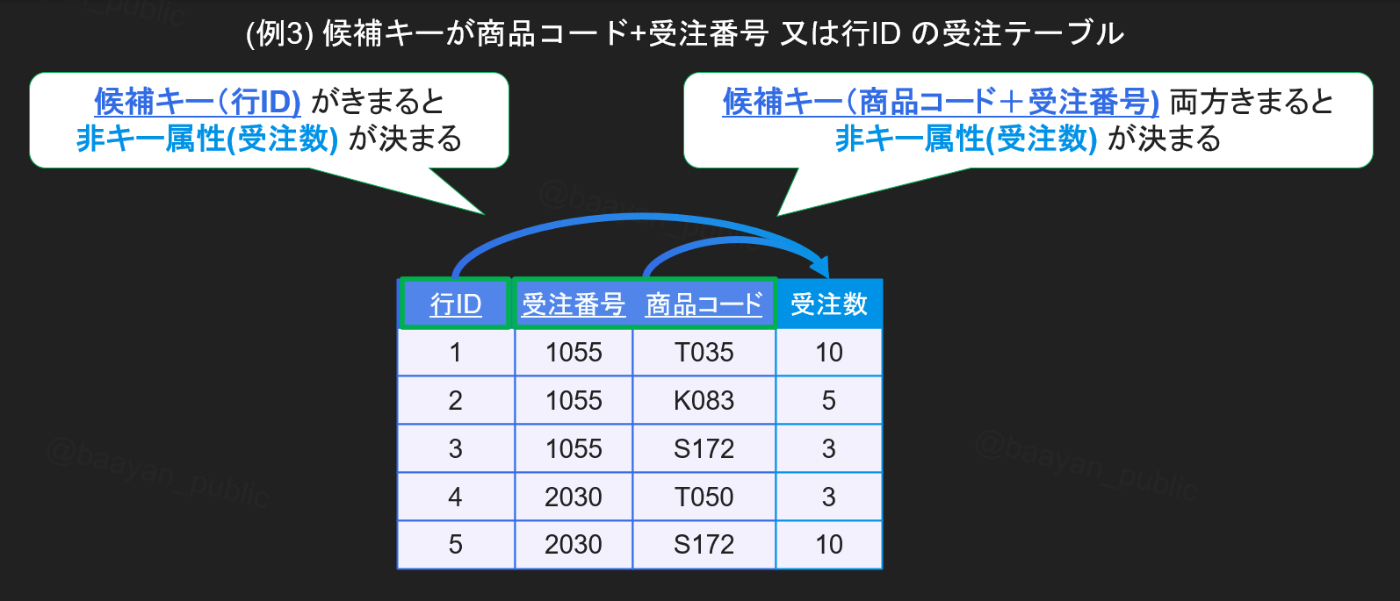
上記は候補キーが複数あった場合です。第2正規系の条件を満たすためには各候補キー全てに対し部分関数従属がないようにしないといけません。
考え方は単純でそれぞれの候補キーで考えていきます。
- 非キー属性(受注数)は候補キー1(商品コード+受注番号)に完全関数従属している。
- 非キー属性(受注数)は候補キー2(行ID)に完全関数従属している。
上記からこの表はいずれの候補キーに対しても部分関数従属がないといえます。
部分関数従属(Partial Functional Dependency:PFD)の例
非キー属性が候補キーに対し部分関数従属している例を説明していきます。
部分関数従属の例
- 候補キー: 商品コード+受注番号
- 非キー属性: 受注数、単価
- FD:(商品コード+受注番号) → 受注数
- FD:商品コード→単価

上記は部分関数従属の例です。候補キー(商品コード+受注番号)に対し、その部分集合(一部)の商品コードだけで、単価は決まります。
このとき
「非キー属性(単価)は候補キー(商品コード+受注番号)に部分関数従属している」
といいます。
ちなみに、非キー属性の 受注数 は 候補キー の 商品コードと受注番号 両方が決まって、はじめて定まるので、候補キーに対し完全関数従属しています。
まとめ
今回は部分関数従属と完全関数従属について取り扱いました。
第2正規系を理解するには候補キー、非キー属性、完全関数従属、部分関数従属を理解する必要がありますので、少し遠回りをしました。
次回からまた正規化のステップを解説していきます!
以上、ばーやんでした!
Discussion