🏫

学校のクラス分けの最適化: Python MIP で解く

2023/12/19に公開

Python

mip

tech

1. はじめに

1-1. 目的

こんにちは！この記事では、私たちがゼミの演習で行った面白いプロジェクトについて話します。プロジェクトのテーマは「クラス分けの最適化」で、Pythonを使って実際にどうやってクラスを上手に分けるかに挑戦しました。学校のクラスを分ける時に、いろいろな条件をどう満たすかって結構頭を使う問題ですよね。そこで、私たちは生徒の学力、性別、リーダーシップ能力などの様々な要素を考慮して、8つのクラスに生徒を公平に割り振る方法を考えてみました。

このプロジェクトの目標は、教育現場でよくある課題、つまりクラス編成の公平性と効率性を向上させることです。私たちは、特別な支援が必要な生徒の適切な配置や、特定の生徒同士を分けるなどの制約も考えながら、最適なクラス分けがどうすればできるかを模索しました。

この記事では、私たちがどのようにしてこの問題に取り組んだのか、そしてどんな解決策を見つけ出したのかを共有します。ゼミでのこの演習は、プログラミングと数理最適化の知識を実際の問題解決に活かす良い機会でした。それでは、私たちのプロジェクトの旅にお付き合いください！

1-2. 主な使用技術

プロジェクトで使用した技術について詳しく説明します。私たちは、クラス分けの最適化アルゴリズムを構築するために、以下の主要なPythonライブラリを活用しました：

mip (Mixed Integer Programming): このライブラリは、最適化問題のモデリングと解決に使います。クラス分けにおける多様な制約を数理モデルに組み込み、最適な解を見つけるのに不可欠でした。
pandas: データ操作と分析に非常に強力なライブラリです。生徒のデータやクラスの特性を効率的に処理し、アルゴリズムに必要なデータ形式に整えるために使用しました。
pydantic: このライブラリは、データの型安全性を保証し、エラーを減らすために使います。生徒データなどの入力が適切な形式と内容を持っていることを確認するのに役立ちます。しかし、後から思い返せば、いらなかったかも？
matplotlib: 可視化ツールとして非常に役立ちます。アルゴリズムの結果を視覚的に表示し、クラス分けの分布やバランスを分かりやすくするために使用しました。
pandera: データのバリデーションに特化したライブラリで、読み込んだデータが期待する仕様に適合しているかをチェックするために使用しました。これにより、データ処理の過程での誤りを未然に防ぐことができました。

これらの技術を駆使して、私たちはクラス分けの最適化問題に取り組むことができました。各ライブラリの特性を活かし、複雑なデータセットと制約条件を効果的に扱うことで、最適化アルゴリズムの開発と実装を行いました。

2. 最適化問題の作成

2-1. 問題設定

ゼミの演習で取り組んだこのプロジェクトでは、以下のような最適化問題を設定しました。私たちの目標は、学校におけるクラス分けをより効果的かつ公平に行うための方法を見つけることです。問題の主な条件は次の通りです：

クラス数：全8クラス
生徒の割り当て：全学生をそれぞれ1つのクラスに割り当てる
生徒数の均等化：各クラスの生徒数をできるだけ均等にする
性別の均等化：各クラスの男女の人数もできるだけ均等にする
学力の均等化：各クラスの学力もできるだけ均等にする
リーダー気質の学生の均等配分：各クラスにリーダー気質の学生をできるだけ均等に割り当てる
特別な支援が必要な生徒の分散：特別な支援が必要な生徒はできるだけ分散させて割り当てる
特定ペアの学生の分離：特定ペアの学生は同じクラスに割り当てない

さらに、オリジナルの要素として、クラス内の学力分布に特に着目しました。単に平均スコアを取るのではなく、クラス内の学力の分布を広げることで、より公平かつ効果的な学習環境を提供することを目指しました。これは、クラス内の学力レベルが一定の範囲内に収まることを保証するため、学力の高い生徒と低い生徒をバランスよく各クラスに配分することを意味します。このアプローチにより、クラス内での相互学習の機会を増やし、教師の負担も均等に分散することができると考えました。

これらの制約を考慮に入れながら、最適なクラス分けのアルゴリズムを設計することが、このプロジェクトの主な挑戦でした。

2-2. データの取得と加工

プロジェクトのデータ処理の部分では、まず生徒と特定ペアのデータを取得し、それらを適切に加工する必要がありました。これは、最適化アルゴリズムに適切な入力を提供するための重要なステップです。以下のコードスニペットは、このプロセスの主要な部分を示しています。

import pandas as pd
import schemas

# 生徒データの読み込みとバリデーション
s_df = pd.read_csv("data/students.csv")
s_df = schemas.validate_students(s_df, len(C))

# 特定ペアのデータの読み込みとバリデーション
pair_df = pd.read_csv("data/student_pairs.csv")
pair_df = schemas.validate_student_pairs(pair_df)

# データの準備
data = prepare_data(s_df, pair_df)

データスキーマの定義

生徒データと特定ペアのデータのバリデーションには、panderaライブラリを使用しました。これにより、データが期待する仕様に適合しているかどうかを確認し、データ処理の正確性を保証しました。

`Student` スキーマクラス

Student スキーマクラスは、生徒データの構造を定義します。各生徒は一意のID、性別、入試スコア、リーダー気質の有無、特別支援の必要性に関するフラグを持っています。これにより、生徒データが適切な形式であることを保証します。

import pandera as pa
from pandera.typing import DataFrame, Series

class Student(pa.SchemaModel):
    student_id: Series[int] = pa.Field(unique=True)
    gender: Series[int] = pa.Field(isin=([0, 1]))
    score: Series[int] = pa.Field(ge=0, le=500)
    leader_flag: Series[int] = pa.Field(isin=([0, 1]))
    support_flag: Series[int] = pa.Field(isin=([0, 1]))

    class Config:
        strict = True

def validate_students(df: DataFrame, num_classes: int) -> DataFrame:
    assert len(df) >= num_classes * 2, "学生数はクラス数の2倍以上である必要があります"
    return Student.validate(df)

`Pair` スキーマクラス

Pair スキーマクラスは、特定ペアのデータの構造を定義します。これには、同じクラスに割り当ててはならない学生のペア情報が含まれています。

import pandera as pa
from pandera.typing import DataFrame, Series

class Pair(pa.SchemaModel):
    student_id1: Series[int] = pa.Field()
    student_id2: Series[int] = pa.Field()

    class Config:
        strict = True

def validate_student_pairs(df: DataFrame) -> DataFrame:
    return Pair.validate(df)

生徒データ (`students.csv`) の概要

student_id: 学生ID
gender: 性別（0: 女性, 1: 男性）
score: 入試の点数（0～500点）
leader_flag: リーダー気質フラグ（1: リーダ気質, 0: それ以外）
support_flag: 特別支援フラグ（1: 特別支援が必要, 0: それ以外）

特定ペアデータ (`student_pairs.csv`) の概要

student_id1: 特定ペアの片方の学生ID
student_id2: 特定ペアのもう片方の学生ID

了解しました。以下に、データの前処理と OptimizationData クラスの詳細な説明を追加します。

データの前処理

以下の関数は、生徒情報とペア情報を処理し、最適化問題で使用するためのデータ構造に変換します。

import pandas as pd
from src import schemas

def prepare_data(s_df: pd.DataFrame, pair_df: pd.DataFrame) -> schemas.OptimizationData:
    # 学生IDを格納したリスト
    S = s_df["student_id"].tolist()

    # 女性学生のIDを格納したリスト
    F = [row["student_id"] for index, row in s_df.iterrows() if row["gender"] == 0]

    # 男性学生のIDを格納したリスト
    M = [row["student_id"] for index, row in s_df.iterrows() if row["gender"] == 1]

    # 辞書（key: 学生ID, value: スコア）
    score = {row["student_id"]: row["score"] for index, row in s_df.iterrows()}

    # 辞書（key: 学生ID, value: リーダーフラグ）
    leader = {row["student_id"]: row["leader_flag"] for index, row in s_df.iterrows()}

    # 辞書（key: 学生ID, value: サポートフラグ）
    support = {row["student_id"]: row["support_flag"] for index, row in s_df.iterrows()}

    # 特定ペアの学生IDsのタプルを格納したリスト
    pair = [
        (row["student_id1"], row["student_id2"]) for index, row in pair_df.iterrows()
    ]

    return schemas.OptimizationData(S, F, M, score, leader, support, pair)

`OptimizationData` クラスの定義

OptimizationData クラスは、最適化問題で使用するデータを格納するためのクラスです。このクラスには、以下の属性が含まれます。

S: 全学生のIDのリスト
F: 女性学生のIDのリスト
M: 男性学生のIDのリスト
score: 各学生のスコアを格納した辞書
leader: 各学生のリーダーフラグを格納した辞書
support: 各学生のサポートフラグを格納した辞書
pair: 特定ペアの学生IDのタプルを格納したリスト

これらの属性は、クラス分けの最適化問題を解く際に必要な様々な情報を提供します。

from typing import Dict, List, Tuple

class OptimizationData:
    def __init__(
        self,
        S: List[str],
        F: List[str],
        M: List[str],
        score: Dict[str, int],
        leader: Dict[str, bool],
        support: Dict[str, bool],
        pair: List[Tuple[str, str]],
    ):
        self.S = S
        self.F = F
        self.M = M
        self.score = score
        self.leader = leader
        self.support = support
        self.pair = pair

このデータ構造は、最適化アルゴリズムに入力するために必要な情報を整理し、効果的なクラス分けのための基礎を提供します。

このようにして、クラス分けの最適化アルゴリズムに必要なデータを準備しました。次のステップでは、これらのデータを使用して、各種制約条件を考慮した最適化モデルを構築します。

2-3. 最適化問題の作成

この章では、クラス分けの最適化問題を作成するプロセスを詳述します。具体的には、minimum_constraints 関数を用いて、生徒の特性に基づいて最適なクラス分けを実現するための制約条件を設定し、最適化モデルを構築します。

最適化モデルの構築

まず、Model クラスのインスタンスを作成します。このインスタンスは最適化問題を表現し、解決するための基盤となります。

`minimum_constraints.py`の全体コード

from typing import List, Tuple
from mip import Model, minimize, xsum
from src import schemas

def minimum_constraints(
    data: schemas.OptimizationData, C: List[str]
) -> Tuple[Model, dict]:
    n = len(data.S)  # n: 学生数

    SC = [(s, c) for s in data.S for c in C]  # 学生IDとクラス名のタプルを格納したリスト

    p = Model("assignment")

    # 決定変数の定義
    x = {}
    for s, c in SC:
        x[s, c] = p.add_var("x({},{})".format(s, c), var_type="B")

    # 目的関数の設定
    p.objective = minimize(xsum(x[s, c] for s in data.S for c in C))

    # 制約の設定
    # 各学生は1つのクラスに割り当てられる
    for s in data.S:
        p += xsum(x[s, c] for c in C) == 1  # 各学生は1つのクラスに割り当てられる

    # 各クラスの生徒数はできるだけ均等にする
    for c in C:
        p += xsum(x[s, c] for s in data.S) >= n // len(C)
        p += xsum(x[s, c] for s in data.S) <= (n // len(C)) + 1

    # 各クラスの男性の人数をできるだけ均等にする
    for c in C:
        p += xsum(x[s, c] for s in data.M) >= len(data.M) // len(C)
        p += xsum(x[s, c] for s in data.M) <= (len(data.M) // len(C)) + 1

    # 各クラスの女性の人数をできるだけ均等にする
    for c in C:
        p += xsum(x[s, c] for s in data.F) >= len(data.F) // len(C)
        p += xsum(x[s, c] for s in data.F) <= (len(data.F) // len(C)) + 1

    # 各クラスの学力をできるだけ均等にする
    total_score = sum(data.score.values())
    for c in C:
        p += xsum(data.score[s] * x[s, c] for s in data.S) >= total_score // len(C)
        # p += xsum(score[s] * x[s, c] for s in S) <= (total_score // len(C)) + 1
        p += xsum(data.score[s] * x[s, c] for s in data.S) <= (
            total_score // len(C)
        ) + max(data.score.values())

    # 各クラスにできるだけ均等にリーダー気質の学生を割り当てる
    total_leaders = sum(data.leader.values())
    for c in C:
        p += xsum(data.leader[s] * x[s, c] for s in data.S) >= total_leaders // len(C)
        p += (
            xsum(data.leader[s] * x[s, c] for s in data.S)
            <= (total_leaders // len(C)) + 1
        )

    # 特別な支援が必要な生徒はできるだけ分散させて割り当てる
    total_support = sum(data.support.values())
    for c in C:
        p += xsum(data.support[s] * x[s, c] for s in data.S) >= total_support // len(C)
        p += (
            xsum(data.support[s] * x[s, c] for s in data.S)
            <= (total_support // len(C)) + 1
        )

    # 特定ペアの学生は同じクラスに割り当てない
    for s1, s2 in data.pair:
        for c in C:
            p += x[s1, c] + x[s2, c] <= 1

    return p, x

制約条件の設定

最適化問題において、以下の制約条件を設定しました：

各生徒は1つのクラスに割り当てられる：各生徒がただ1つのクラスにのみ割り当てられるように制約します。
各クラスの生徒数の均等化：各クラスの生徒数ができるだけ均等になるように制約します。
性別の均等化：各クラスにおける男女の人数が均等になるように制約します。
学力の均等化：各クラスの学力が均等になるように、総スコアを基に制約を設定します。
リーダー気質の学生の均等配分：リーダー気質を持つ学生が各クラスに均等に割り当てられるように制約します。
特別支援が必要な生徒の分散：特別な支援が必要な生徒が各クラスに均等に分散されるように制約します。
特定ペアの学生の分離：特定ペアの学生が同じクラスに割り当てられないように制約します。

最適化モデルの利用

最適化モデルは以下のようにして利用されます。

C = ["A", "B", "C", "D", "E", "F", "G", "H"]
model, x = optimizer.minimum_constraints(data, C)

ここで C は利用可能なクラスのリストを表し、minimum_constraints 関数は、与えられた生徒データとクラスに基づいて最適化モデルを構築します。

2-4. オリジナルの最適化問題の作成

この章では、ゼミの演習でのオリジナル要素を加えたクラス分け最適化問題を作成します。ここでは、生徒の学力に基づくスコア分布の均一化に注目しました。

学力分布の均一化の重要性

クラスにおける学力の平均スコアだけではなく、スコアの分布に着目することで、より公平な教育環境を作り出すことができます。例えば、平均スコアが50点のクラスがあり、その中に0点、50点、100点のスコアを持つ生徒がいる場合、このクラスは幅広い学力レベルを持つ生徒で構成されていると言えます。これに対し、全員が50点のスコアを持つクラスは、学力レベルが非常に均一です。このような均一化された環境では、学生同士の相互学習の機会が減少する可能性があります。したがって、学力の偏差をある程度保持することで、より豊かな学習環境を提供することが可能です。

最適化問題へのオリジナル要素の組み込み

この思想に基づき、以下の関数を使用して最適化モデルにオリジナルの制約を追加します。具体的には、クラス内での学力スコアの上位者と下位者をそれぞれ異なるクラスに割り当てるように設計します。

from mip import Model, xsum

def add_balanced_assignment_constraint(
    model: Model, x: dict, scores: dict, classes: list, students: list
):
    sorted_students = sorted(students, key=lambda s: scores[s])
    num_classes = len(classes)

    for i in range(num_classes):
        # 上位と下位から学生を選び、それぞれを異なるクラスに割り当てる
        top_student = sorted_students[i]
        bottom_student = sorted_students[-i - 1]
        model += xsum(x[top_student, c] for c in classes) == 1
        model += xsum(x[bottom_student, c] for c in classes) == 1
        model += xsum(x[top_student, c] + x[bottom_student, c] for c in classes) == 2

    return model

このアプローチにより、各クラスは学力レベルが異なる生徒を含むことになり、クラス内の学力分布の偏差を保つことができます。これは、生徒たちにより多様な学習機会を提供し、教育の質を向上させることを目的としています。

最適化問題の実行

今までの制約条件から最適化問題を実行します。

model.optimize()

3. グラフの作成

この章では、最適化モデルの結果を視覚化するために、ヒストグラムとボックスプロットを作成します。これにより、最適化によって得られた各クラスの学力スコアの分布を詳細に分析できます。

3-1. ヒストグラムの作成

ヒストグラムは、各クラスに割り当てられた生徒のスコア分布を示すのに適しています。以下のコードは、モデルの最適化後に各クラスのスコアデータを取得し、ヒストグラムを描画する方法を示しています。

import matplotlib.pyplot as plt
import numpy as np

# 各クラスのスコアのヒストグラムを描画
for c, scores in class_scores.items():
    plt.hist(scores, bins=10, alpha=0.5, label=c)
    # 統計情報の出力
    print(f"Class {c}:")
    print(f"Mean: {np.mean(scores):.2f}")
    print(f"Median: {np.median(scores):.2f}")
    print(f"Standard Deviation: {np.std(scores):.2f}")
    print(f"Min: {np.min(scores):.2f}")
    print(f"Max: {np.max(scores):.2f}")
    print(f"Range: {np.max(scores) - np.min(scores):.2f}")
    print("-" * 30)

plt.legend(loc="upper right")
plt.savefig("image/normal_histogram.png")

# pyplotインスタンスをクリア
plt.clf()

ヒストグラム以外にも、各クラスのスコアの平均、中央値、標準偏差、最小値、最大値、範囲などの統計情報を確認できます。

3-2. ボックスプロットの作成

ボックスプロットは、各クラスのスコア分布のばらつきや中央値を視覚的に比較するのに役立ちます。以下のコードは、各クラスのスコアデータを用いてボックスプロットを描画する方法を示しています。

# ボックスプロットの描画
plt.figure(figsize=(10, 6))
plt.boxplot(class_scores.values(), labels=class_scores.keys())
plt.savefig("image/normal_boxplot.png")

ボックスプロットにより、各クラス間のスコア分布の違いをより明確に把握できます。これにより、最適化モデルがどのように各クラスの特性を反映しているかを評価することが可能です。

データの成型や詳細な最適化モデルのコードについては、後ほど全体のコードを通じて確認してください。これらのグラフを通じて、最適化によるクラス分けの効果をより深く理解することができます。

4. 結果の分析と視覚化

この章では、制約条件を追加したことによるクラス分けの変化を、統計量と視覚資料を用いて分析します。

制約追加前後のクラス別スコア分布の比較

制約を加えた結果、クラスごとのスコア分布に以下のような変化が見られました：

統計量	Class A	Class B	Class C	Class D	Class E	Class F	Class G	Class H
Mean (制約前)	309.46	309.46	301.73	301.75	301.75	301.75	301.80	301.75
Mean (制約後)	309.46	301.75	309.49	301.73	301.77	301.75	301.73	301.77
Median (制約前)	315.00	309.00	303.50	302.00	295.50	314.00	320.00	297.50
Median (制約後)	314.00	303.50	317.00	320.50	297.50	318.50	298.00	309.50
Std Dev (制約前)	54.78	64.91	38.59	57.60	66.65	63.10	71.91	90.25
Std Dev (制約後)	75.79	56.61	63.10	75.06	55.70	73.97	58.05	57.58
Range (制約前)	307.00	265.00	158.00	291.00	350.00	299.00	272.00	397.00
Range (制約後)	342.00	245.00	277.00	397.00	194.00	343.00	232.00	268.00

制約追加前後の統計量を比較すると、特定のクラスで平均スコアが上昇し、標準偏差の増加によりスコアの分散が拡大していることがわかります。これは、クラス内での多様な学習機会の提供や相互学習環境の豊かさに寄与している可能性があります。

クラス別スコア分布の視覚化

最適化によって得られたクラス別のスコア分布を視覚的に理解するために、ヒストグラムとボックスプロットを作成しました。

ヒストグラム

ヒストグラムは、各クラスに割り当てられた生徒のスコア分布を色分けして重ね合わせた形で示しており、クラス間でのスコアの重なり具合や分布の形状を明確に比較することができます。

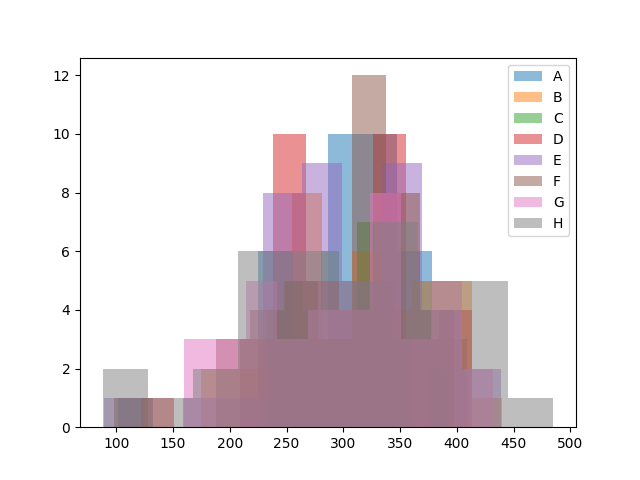
オリジナルの制約条件なし

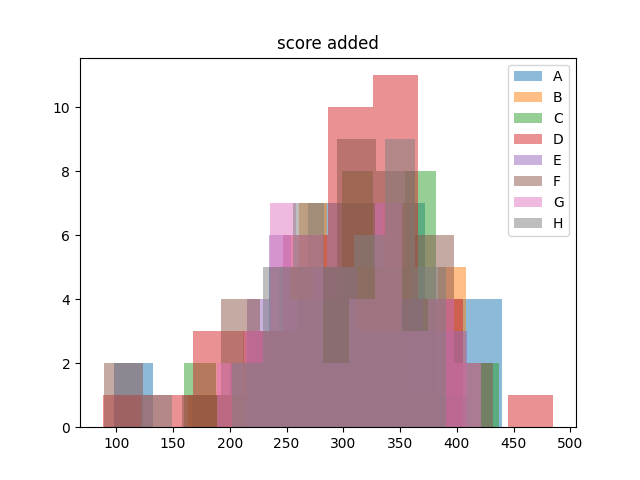
オリジナルの制約条件あり

ボックスプロット

ボックスプロットは、各クラスに割り当てられた生徒のスコア分布のばらつきや中央値を箱形の図で表しています。これにより、クラス間のスコア分布の違いをより明確に把握することができます。

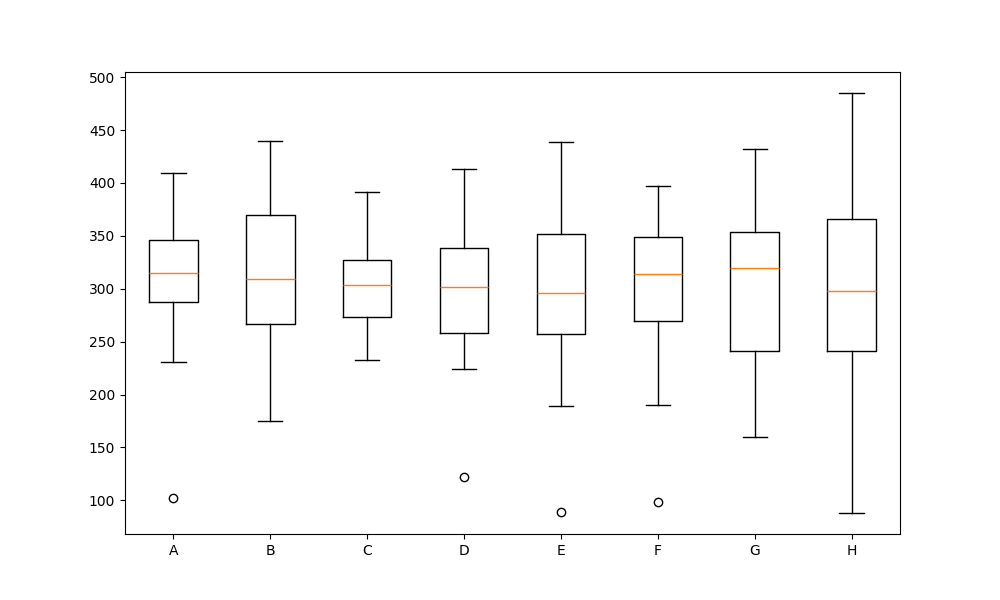
オリジナルの制約条件なし

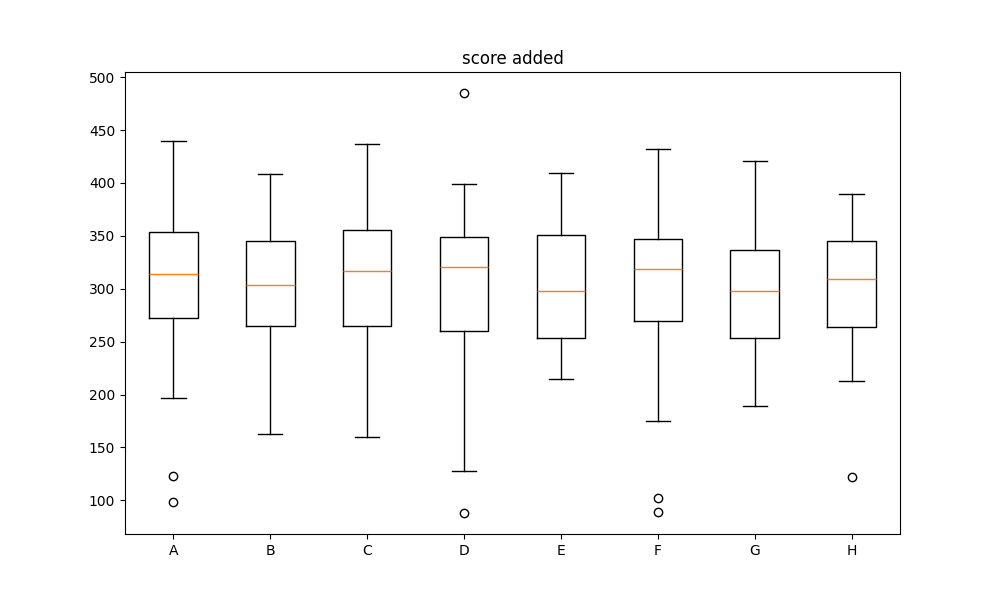
オリジナルの制約条件あり

総合的な考察

制約を追加したことによる統計量と視覚資料の分析から、以下の点が明らかになりました：

制約追加後、各クラスのスコア分布の平均値はわずかに上昇または一定を保ちましたが、分散は全体的に拡大しました。これは、制約によってクラス内の学力レベルが多様化したことを意味し、学習機会の公平性が向上した可能性があります。
中央値の変動は、ほとんど見られなかった。
標準偏差の増加は、クラス内の学力レベルがより幅広くなり、教育環境における多様性と包括性が促進されたことを示しています。
ヒストグラムとボックスプロットの外れ値の増加は、学力の上位者と下位者が各クラスに分配されていることを示しており、制約追加により意図したとおりの効果があったことを反映しています。

総じて、制約を追加したことで、より公平で多様な学力分布を持つクラス編成が実現されたと考えられます。これにより、クラス内での相互教育の機会が拡大し、学生間の協力的学習が促進される可能性が高まります。ただし、劇的な変化があったかと言われればわかりません。

参考資料

今回参考にさせていただいた書籍
「Pythonではじめる数理最適化」の3章を参考にさせていただきました。良書なのでぜひ学習のお供にしてください！！
https://www.amazon.co.jp/dp/B09G9VZ4PH

プロジェクトリポジトリ

今回作成したリポジトリ:

本記事で構築したプロジェクトの全てのコードが含まれています。是非、クローンまたはフォークして、自由に使用や改変を行ってください。

1. はじめに

1-1. 目的

1-2. 主な使用技術

2. 最適化問題の作成

2-1. 問題設定

2-2. データの取得と加工

データスキーマの定義

生徒データ (students.csv) の概要

特定ペアデータ (student_pairs.csv) の概要

データの前処理

2-3. 最適化問題の作成

最適化モデルの構築

制約条件の設定

最適化モデルの利用

2-4. オリジナルの最適化問題の作成

学力分布の均一化の重要性

最適化問題へのオリジナル要素の組み込み

最適化問題の実行

3. グラフの作成

3-1. ヒストグラムの作成

3-2. ボックスプロットの作成

4. 結果の分析と視覚化

制約追加前後のクラス別スコア分布の比較

クラス別スコア分布の視覚化

ヒストグラム

ボックスプロット

総合的な考察

参考資料

プロジェクトリポジトリ

Discussion

生徒データ (`students.csv`) の概要

特定ペアデータ (`student_pairs.csv`) の概要