ニューラルネットの重み行列は理解不能なブラックボックスではない

はじめに

あなたは一般的なニューラルネットについてどこまでの理解を持っていますか？

単層のパーセプトロンの挙動を観察したことはありますか？

MLPの中間層の出力や重み行列を覗いたことは？

あるいはニューラルネットに関してこのように考えていないでしょうか。

ニューラルネットの類は、データから「ときに人間には理解しがたい特徴量を自動抽出する」システムであると。

しかし結論から言えば、NNの重み行列が形成する値は理解不能なブラックボックスではなく、各層のあるときの入力に似た値を各ニューロンが保持している形となります。

内積は一種の類似度計算である

まず前提として、全結合な単層のパーセプトロンが何をしているかおさらいしましょう。バイアスと活性化関数は一旦考えないものとして、全結合層が行っている処理は単に入力と重み行列の行列積計算でした。

$$Outputs = matmul(Inputs, W)$$

行列積計算は、行列の内積とも呼ばれますが、その処理は名の通り前者の行ベクトルと後者の列ベクトルの内積を各列各行について取ったものです。

つまり、行列積計算の結果得られる行列の各要素は、前者の行ベクトルと後者の列ベクトルの内積の値(スカラー値)になるということです。

Inputsを(バッチ,データ)次元の行列、Wを(データ,ニューロン)次元の行列と考えると、計算結果であるOutputsは(バッチ,ニューロン)次元の行列となり、その要素がデータ次元の内積値です。

$$Outputs = \begin{pmatrix} Neuron_{00}, Neuron_{01}, ..., Neuron_{0n} \\ Neuron_{10}, Neuron_{11}, ..., Neuron_{1n} \\ ... \\ Neuron_{b0}, Neuron_{b1}, ..., Neuron_{bn} \\ \end{pmatrix}$$

ところで、内積値とは一体何だったでしょうか。

ベクトルの内積の定義は、同じインデックスにある要素の積の総和でした。

$$a = \sum_{i=0}^n u_{i} v_{i}$$

この値は、ベクトルの各要素について、基本的には互いの形状が似ているほど大きな値を取ります。

$u_{i}$ と $v_{i}$ が 正同士なら正、負同士でも正、正と負あるいは負と正なら負です。

つまり内積はある種の類似度を計算する処理であるということです。(もちろん、sin(x)と5*sin(x))のように形状は同じまま上下に拡大した形同士なら更に大きな値を取ってしまうので、一概には言えませんが)

実際、関数版の内積は、シフト値の無い相互相関関数と同じ形をしています。

$$a = \int_{-∞}^{∞} f(x)g(x) dx$$

$$F(t) = \int_{-∞}^{∞} f(x)g(x+t) dx$$

上が関数同士の内積の定義で、下が関数同士の相互相関の定義です。

なので、内積はシフトを考慮しない、「今の形」同士だけの限定的な相関を取る処理とみなせます。

わかる人にとっては、内積は正規化されていないコサイン類似度であると言ったほうがわかりやすいかもしれません。コサイン類似度は

$$\frac{\vec{u}・\vec{v}}{|\vec{u}||\vec{v}|}$$

ですね。

各層の重み行列はその層の入力に近づく

さて、ここまで行列積の計算が一種の類似度計算(というか相関値そのもの)であることは説明しました。

ではそれをもって何が言えるかというと、パーセプトロンはこの入力と重み行列の相関値が理想出力そのものになるよう調整するため、重み行列の各ニューロンはいずれかの入力に近づいていくということです。

これだけでは理解しがたいかと思いますので、もう少し説明を重ねます。

パーセプトロンにおける重みの更新量 $dW$ は、その層の入力をInputs、その層の出力から逆伝播してくる誤差をdoutと置くと、

$$dW = matmul(Inputs^T, dout)$$

でした。実際はこの $dW$ に学習率(Learning Rate)を掛けたものを現在の重みに足す事で調整します。

上記の式は、順伝播が

$$Outputs = matmul(Inputs, W)$$

であったことから、$W$ の出力への影響値、言い換えるなら $Outputs$ の $W$ に対する微分値 $Inputs^T$ に修正すべき影響幅、すなわち $dout$ を掛けたものとなります。

ここで重要なのは、出力が理想出力になるよう $W$ を調整し、その幅は $Inputs$ と $dout$ に依存するという点です。

$dout$ が大きいほど最終的な修正量も大きくなり、それが目指すところはいかなる入力に対しても $dout = 0$ に近づくような重み行列を完成させることです。

$dout$ は、最終層では

$$dout = Outputs - 教師信号$$

です。これは10クラス分類を行う単層のパーセプトロンとone-hotな教師信号を考えたとき、ニューロンの数は出力に対応する10個だけですので、ニューロン列が直接的に教師信号のビットが立っている形を目指すことになります。これは例えば、

$$Outputs = \begin{pmatrix} 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 \\ 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 \\ ... \\ 0, 1, 0, 0, 0, 0, 0, 0, 0, 0 \\ \end{pmatrix}$$

のような形を目指す、ということです。列はバッチ中の各入力に対応する出力として、各行がクラスを分類した結果立っているビットを表しています。

さて、このOutputsは入力との相関値列でもあるのでした。入力との相関値がこうなるよう重みを学習するということは、たとえば上記のOutputs例の一行目を取り出すと、

$$\begin{pmatrix} Neuron_{00}, Neuron_{01}, ..., Neuron_{0n} \end{pmatrix}$$

$$\begin{pmatrix} 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 \end{pmatrix}$$

この両者が一致するように学習するということであり、つまり今回の理想出力クラスが0であるときは、$Neuron_{00}$ が1で $Neuron_{01} から Neuron_{0n}$ が0になるように学習するということです。

$Neuron_{00}$ は 入力の行0と重み行列の列0なベクトル同士の内積でしたので、この内積が1になるよう学習するということは、入力と重みの一部がある程度の正の相関を示すように重みを更新するということです。

また他のニューロンについて、この内積が0になるように学習するということは入力と重みの一部が無相関を示すように重みを更新するということです。

これは言い換えれば、行列の一部を現在の入力と似るように、他の箇所を似ないように重みを更新するのがパーセプトロンである、ということです。

多層化した場合について

いまは単層のパーセプトロンについて考えましたが、多層化してもやることは一緒です。少なくとも最終層の出力パターンは教師信号そのものに寄せていかなければならないので、最終層では全く同様の処理が必要となります。

中間層はビット列を出力しないのでこの考え方は通用しないのではないか？と思われるかもしれませんが、誤差逆伝播は

$$dout_i = matmul(dout_{i+1}, W_{i+1}^T)$$

のように伝播していくので、中間層にとって教師信号に相当する値は、出力層の $dout$ が

$$dout = Outputs - 教師信号$$

であったことから考えて、

$$教師信号_i = Outputs_i - dout_i = Outputs_i - matmul(dout_{i+1}, W_{i+1}^T)$$

となるはずです。つまり中間層は教師信号を後の層から伝わる形で持っているというだけで、教師信号は存在しています。もはやビット列で無いとしても、正負を持ったある値で指定されると考えられます。

さらに言えば、中間層と出力層の間にReLUのような活性化関数が挟まれているなら、後ろの層から伝わる $dout_i$ は、負の値がReLUの微分(<0のときに0)により切られ、単に正の相関と0によるものとなっているはずです。

追記訂正。doutが正と0だとしても、重みにより符号は変わりうるし、そもそもOutputsから引かれているので、理想出力が正の相関と0になるとは限らないかもしれない。

結果として、中間層の重み行列もまた、入力・重み行列の行列積の計算結果が正の相関と0になるように学習、つまりは重みの一部があるときの入力に似るように調整されるというわけです。

追記訂正。上と同様に、負の相関を示さないとは一概に言えないと思われる。

コード

これまでの説明が妄想でないことを示すため、確認用のコードと生成した画像を載せておきます。

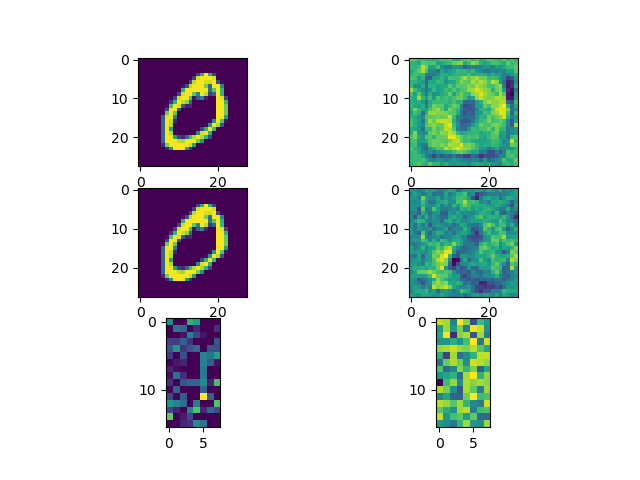
この画像を生成します。

すみません、これ確認して一気に自信なくなってきました。妄想かも。

・上、単層なパーセプトロンの、0を入力したときに一番高い相関を示した重み行列の一部
・中、3層パーセプトロンの中間層で同様に取った重み行列の一部
・下、出力層で同様に取った重み行列の一部(128次元を無理やり画像化)

中間層の表現ですが、直接的にラベルのone-hotと対応していた単層の場合とは異なり、教師信号の一部が後の層からの逆伝播に依存した値となっているため、鮮明に0のテンプレートを示しはしませんが、入力と何らかの形で似た値が形成されているのはわかると思います。

下の出力層の表現については、値の幅が変わっているため大きく異なるように見えますが、元々輝度の高い点が同じ位置に表れていたりと、全体が盛り上がっているだけで形状はなんとなく似たものとなっているのがわかります。

Python3 Tensorflow2.5

weight_slp_mlp.py

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt


if __name__ == '__main__':
    tf.random.set_seed(12345)

    epochs = 20
    batch_size = 500

    dataset = tf.keras.datasets.mnist
    (train_images, train_labels), (test_images, test_labels) = dataset.load_data()

    train_images = train_images / 255.0
    test_images = test_images / 255.0

    train_images = train_images.reshape((-1, 28 * 28))
    test_images = test_images.reshape((-1, 28 * 28))

    slp_0 = tf.keras.layers.Dense(10, activation='softmax')
    slp = tf.keras.Sequential([
        tf.keras.layers.InputLayer(train_images[0].shape),
        slp_0
    ])

    slp.compile(optimizer='adam',
                loss='sparse_categorical_crossentropy',
                metrics=['accuracy'])

    mlp_0 = tf.keras.layers.Dense(128, activation='relu')
    mlp_1 = tf.keras.layers.Dense(10, activation='softmax')
    mlp = tf.keras.Sequential([
        tf.keras.layers.InputLayer(train_images[0].shape),
        mlp_0,
        mlp_1
    ])

    mlp.compile(optimizer='adam',
                loss='sparse_categorical_crossentropy',
                metrics=['accuracy'])

    slp.fit(train_images, train_labels, epochs=epochs, validation_split=0.02, batch_size=batch_size)
    mlp.fit(train_images, train_labels, epochs=epochs, validation_split=0.02, batch_size=batch_size)

    x = train_images[1:2]
    y_slp = slp_0(x).numpy()
    winner_neuron_idx_slp = np.argmax(y_slp)  # 最も強い相関を示したニューロンのインデックスを取得
    winner_neuron_slp = slp_0.get_weights()[0][:, winner_neuron_idx_slp]  # 最も強い相関を示したニューロンの重みを取得

    y_mlp_0 = mlp_0(x)
    y_mlp_1 = mlp_1(y_mlp_0).numpy()
    y_mlp_0 = y_mlp_0.numpy()

    winner_neuron_idx_mlp_0 = np.argmax(y_mlp_0)
    winner_neuron_mlp_0 = mlp_0.get_weights()[0][:, winner_neuron_idx_mlp_0]
    winner_neuron_idx_mlp_1 = np.argmax(y_mlp_1)
    winner_neuron_mlp_1 = mlp_1.get_weights()[0][:, winner_neuron_idx_mlp_1]

    plt.subplot(3, 2, 1)
    plt.imshow(x.reshape((28, 28)))
    plt.subplot(3, 2, 2)
    plt.imshow(winner_neuron_slp.reshape((28, 28)))

    plt.subplot(3, 2, 3)
    plt.imshow(x.reshape((28, 28)))
    plt.subplot(3, 2, 4)
    plt.imshow(winner_neuron_mlp_0.reshape((28, 28)))

    plt.subplot(3, 2, 5)
    plt.imshow(y_mlp_0.reshape((16, 8)))  # 128次元を無理やり画像化
    plt.subplot(3, 2, 6)
    plt.imshow(winner_neuron_mlp_1.reshape((16, 8)))

    plt.show()

おわりに

ほぼ完全に持論なので間違ってたらすみません。

追記:中間層の重みが入力とそんなに似ていない問題について、追加として以下の記事を書きました。

ニューラルネットが分散表現を構築する本当の理由