えっTableauってMOD関数ないんですか?という痒いところを解決する話
はじめに
こんにちは。整数を整数で割った余りを求める剰余演算ことMOD関数を,Tableauで全関数探したけどありませんでした。
どうして…
一方で,整数を整数で割った商を求める関数ことDIV関数はあったので,それを使って余りを算出する関数を調べたので,記録として残しておこうと思います。
(2024/07/01追記)
関数でなくて演算子として%があることに今更気付きました……。ただどっちにしろユークリッド除法ではなさそうなので,それを回避するなら一工夫が必要そうです。
過程を省くとこれで書ける
詳細は後述しますが,日本で教わったような正の値としての余り(ユークリッド除法) を実現するには,少し工夫が必要でした。
分かりやすさも兼ねて,以下2式で実現できます。ここで,[mod number]は割る数として整数型のパラメータを使っています。
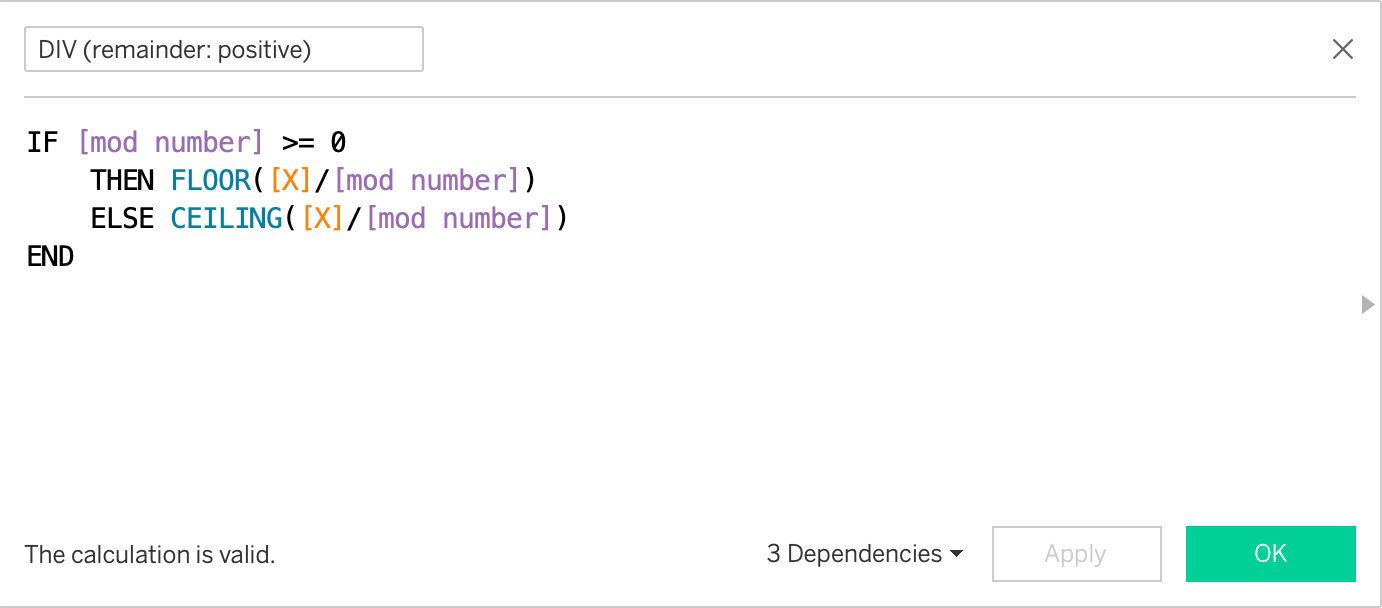
// [DIV (remainder: positive)] =
IF [mod number] >= 0
THEN FLOOR([X]/[mod number])
ELSE CEILING([X]/[mod number])
END
[X] - [DIV (remainder: positive)] * [mod number]

じゃあ「商」と「余り」に作法があるのか
上では工夫を組み込んだ式を書いていますが,なんでそんなことをやる必要があるのかを見ていきます。ご興味あればお付き合いください。自分は知らなかったので驚きました。
Tableauで実装されている関数の出力
割り算を考えるとシンプルに,「(x: 割られる数) = (n: 割る数) * (q: 商) + (r: 余り)」になるはずなので,DIV関数がある以上,余りr(MOD演算で出てくるもの)は以下のように書けるはずです。この場合,「(余り) = (x: 割られる数) - (mod number) * DIV」ですね。
[X] - DIV([X], [mod number]) * [mod number]

では,これまでに書いた関数たちの出力を比較してみましょう。割る数([mod number])はパラメータで3に設定しています。

割られる数が負である部分に違いがあることが分かります。
これに関して,剰余演算についてもう少し調べてみると,どうやら数学的に正しいとされる除法と,アルゴリズム的に効率が良く(?)実装されている除法とが異なる場合があるそうです。
Wikipediaの図が分かりやすかったので引用します。赤線が商,緑線が余りです。

要は,余りrが割る数nと比べて0<=r<nであるのが馴染みのある剰余演算(ユークリッド除法。WikipediaでいうとEuclidean division)と,Tableauで実装されている除法(WikipediaでいうとTruncated division)とはルールが微妙に違います。
- 前者は余りが常に正となるようにするのがルールです。数学的に正しいとされているのはこちらのようです。
- 後者はTruncatedとあるように,「(
n: 割る数) * (q: 商)」の結果の絶対値が「(x: 割られる数)」の絶対値を超えないように切り捨てられています。割られる数が正の場合余りが正,また,割られる数が負の場合余りが負になっています。ユークリッド除法での余りは常に正になるように調整されているので,Tableauでそれを実装するためには,割られる数の正負に応じて計算方法を切り替える必要がありました。そのため冒頭の式につながります。割られる数が負の場合は余りが負にならないよう,大きめに(CEILINGで切り上げて)商を算出してもらう必要があります。
おわりに
いろいろみていると,MOD関数に複数の種類がある以上,あえてMOD関数を実装せず,FLOOR関数やCEILING関数で使って計算させるままにしておいたほうがいいかもなと思うようになってきました。冒頭に書いた式でも結構シンプルですもんね。
ちなみにBigQueryはMOD関数がありました。なるほどという顔をしています。
余談
現在弊社Rakutenでは,楽天モバイルの社員紹介キャンペーンを実施しております。
下記リンクから楽天会員情報でログインしていただいたあとに手続きを進めると,2024/05/06時点では最大14000楽天ポイントがもらえますので,ご興味ある方は覗いてみてください。
よろしくお願いいたします。
Discussion