仕事に数学を使うということとその楽しさ
どうも。株式会社ウェイブでエンジニアとプロマネをやっている肥沼です。
今日は、仕事で数学の楽しさを再発見した喜びを記事にしたいと思います。
(誰かとこの喜びを共有したい
再発見の内容は
指数関数を積分すれば指数関数に戻る
です。では記事を進めていきたいと思います。
事の発端
私の所属するチームのメンバーに
「過去に売れていたが今売れていない商品を探すのが少し大変化も」
という課題感がありましたので、解決しようと思い立ったのが事の発端です。
「過去に売れていたが今売れていない商品」というのは、売上vs.日付のグラフにするとこんなような商品のこととのことです。
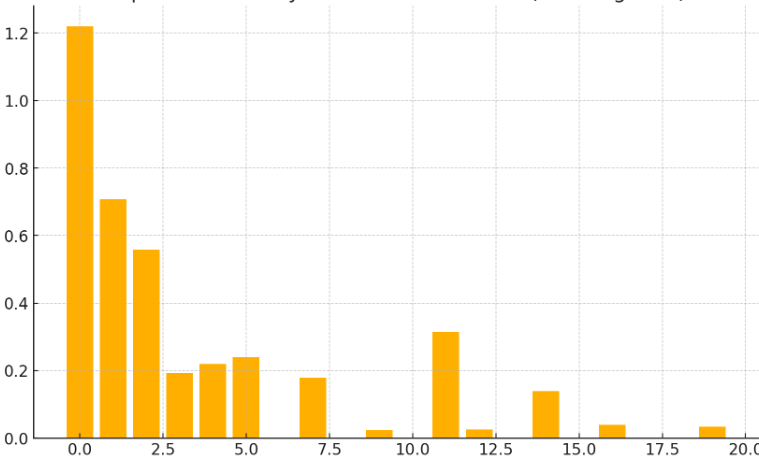
さてこれを見て私は「減衰(収束)系だから指数関数でモデル化できそうだな」と思いやってみることにしました。
そうは簡単にはいかない
モデル式は次の通りにしました。
この式で非線形回帰分析(カーブフィッティング)して出してみるとこんな感じになります。

確かに最も誤差が少なくなるようなフィッティングはできたんですが、思ってたんと違いました。
思ってた結果↓

ならば、極値を基準にフィッティングすればいいじゃん、と思って極値を出してみたり、移動平均出してみたり、周波数空間での分析してみたんですが、ハイパーパラメータが多くなりすぎでうまくいかなかったのです。
ノイズ(真のノイズとは異なるが、ノイズとして扱ってみた)が厄介なので、
ノイズがいやなら積分すればいいじゃない
(こんな格言とかはありません
という声が脳内に響いたので、積分してみました。
積分してノイズを減らした結果
積分(累積和)をするとこうなります。
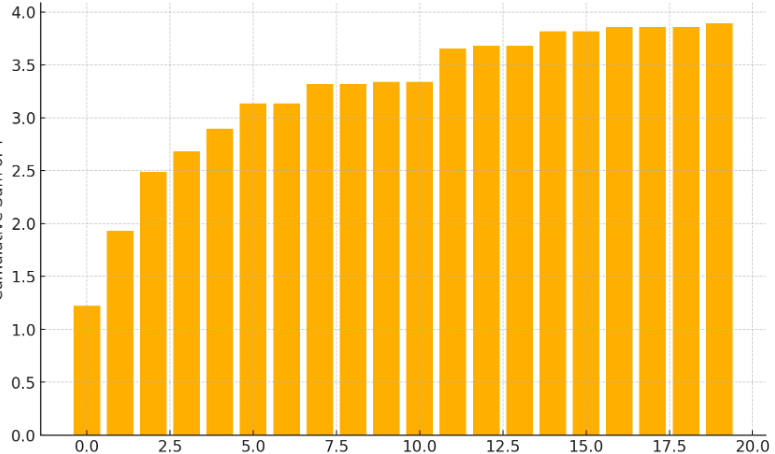
ガタガタさがなくなりました!
(売り上げは常に正なので、累積の場合かならず単調増加になり、ノイズの影響を減らすことができる
このグラフも減衰(収束)系だから指数関数でモデル化できる!さっきよりいけそうと思いました。
この減数系ならさっきのモデルよりいい感じのモデル(必ず原点を通るといういい制約のモデル)にできるので、キタコレって感じです。
ん? まて、
指数関数を積分したら、そりゃ指数関数になるの当たり前じゃん!
を再発見してしまいました。はい、感動しました。数学の知識が、実生活と結びつきました。楽しいですねぇ。。。
上記の式ですんなりフィッティングできたので、あとは商品ごとに時定数tauの大きい順に並べれば「過去に売れていたが今売れていないランキング」的なのが完成というわけです。
まとめ
すごい変なことに楽しみを感じる筆者でした。
Discussion