RustでMerge Sort
はじめに
Rustで、入力の配列を半分にしながら再帰的にソートするMerge Sortを実装してみる。Rustは所有権や借用にうるさい言語なので実装できるか?という観点での練習。
シングルスレッドでの実装
fn _merge<T: Ord + Copy + Default> (left: &[T], right: &[T]) -> Vec::<T> {
let (mut i, mut j, mut k) = (0, 0, 0);
let mut work_vector: Vec<T> = vec![T::default(); left.len() + right.len()];
while i < left.len() && j < right.len() {
if left[i] < right[j] {
work_vector[k] = left[i];
i = i + 1;
} else {
work_vector[k] = right[j];
j = j + 1;
}
k = k + 1;
}
if i < left.len() {
work_vector[k..].copy_from_slice(&left[i..]);
} else {
work_vector[k..].copy_from_slice(&right[j..]);
}
work_vector
}
fn merge_sort<T: Ord + Copy + Default> (data: &mut [T]) {
if data.len() < 2 {
return
}
let mid = data.len() >> 1;
merge_sort(&mut data[..mid]);
merge_sort(&mut data[mid..]);
let sorted = _merge(&data[..mid], &data[mid..]);
data.copy_from_slice(&sorted);
}
mainの例はこんな感じ
fn main() {
let mut vec: Vec<u64> = vec![5, 4, 10, 2, 7];
merge_sort(&mut vec);
println!("{:?}", vec);
}
意外とすんなり実装できた。基本的にスライスを渡していくのだが、変更可能な借用(mutable borrow)は1つしかできないという決まりがある。ただ、再帰的に次々とmerge_sortに渡していく感じなので、この規則は問題にならない。また、変更不可能な借用(immutable borrow)はいくらでもいいので、_mergeへの引数は、同じスライスのサブセットを渡して問題がない。ここが
let sorted = _merge(&mut data[..mid], &mut data[mid..]);
こんな感じで変更可能な借用をしようとすると怒られる。
昔 Merge SortをRustで書こうとした時は苦労した記憶があるのだけど、あっさり書けてしまった。
マルチスレッドでの実装
Merge Sortといえば並列化。分割した配列はそれぞれ独立して処理できるので、スレッドを割り当てると速くなる。ただ、Rustの場合は借用の話がでてくる。
fn parallel_merge_sort<T> (data: &mut Vec<T>)
where T: Ord + Copy + Default + Send + 'static
{
let thread_num = thread::available_parallelism().unwrap().get();
let mut handles = Vec::<thread::JoinHandle<Vec<T>>>::new();
for i in (1..=thread_num).rev() {
let offset = data.len() - (data.len() / i);
let mut work_vector = data.split_off(offset);
let handle = thread::spawn(move || {
merge_sort(&mut work_vector);
work_vector
});
handles.push(handle);
}
let mut sorted_vectors = Vec::<Vec<T>>::new();
for handle in handles {
let result = handle.join().unwrap();
sorted_vectors.push(result);
}
while sorted_vectors.len() > 1 {
let mut remains = std::mem::take(&mut sorted_vectors);
while remains.len() > 1 {
let left = remains.pop().unwrap();
let right = remains.pop().unwrap();
let sorted = _merge(&left, &right);
sorted_vectors.push(sorted);
}
if remains.len() == 1 {
sorted_vectors.push(remains.pop().unwrap());
}
}
data.append(&mut sorted_vectors.pop().unwrap());
}
シングルスレッド版の関数を活用して、あっさりと実装できてしまった。Rustでのスレッド処理がいくつかあるが、spawnでスレッドを立てて、JoinHandleの返り値で結果を得るという、他言語でもよくあるパターンを使った。
配列の分割
基本的にはthread::available_parallelism()で得られるコア数に配列を分割し、それぞれスレッドを立てて実行させる。
各スレッドに配列のスライスを渡せればいいのだが、所有権の問題がでてくるのでsplit_off(at:)で分割して渡している。これはatの位置以降の要素を切り離して別のvectorにしてくれる関数。所有権などもよしなに処理してくれるとあるが、試してみるとメモリの位置が新しくなっているので、コピーしているっぽい。実際、結構処理コストは高い関数である。
let mut data :Vec<u8> = vec![0, 1, 2, 3, 4];
println!("{:p} {:p}", &data[0], &data[3]);
let off = data.split_off(3);
println!("{:p} {:p}", &data[0], &off[0]);
0x15b605e50 0x15b605e53
0x15b605e50 0x15b6060d0
offsetを0にすると、vectorのコピーをしてdataの方を空行列にしてくれる。それを利用してループを使って行列を分割している。
所有権の移譲
各スレッドで計算した配列はsorted_vectorsに集めて、後ろのwhileで2つずつマージしている。ここではうまく所有権の移動で処理できているので複製は発生していない。
また、以下の部分。mem::take(dst:)は、dstを初期値(Vecの場合は空行列)にするとともに、元のdstの所有権を返すという関数。
let mut remains = std::mem::take(&mut sorted_vectors);
なので、ここはsorted_vectorsの所有権をremainsに渡し、sorted_vectorsを空行列にする。という意味になる。以下と同じではあるが、すっきり書ける。
let mut remains = sorted_vectors;
sorted_vectors = Vec::new();
速度の計測
マルチスレッドの効果を確かめるために、速度の計測を行なった。動作させたのは8コアのCPUで、ソート対象はVec<u64>とした。マルチスレッドはスレッド数を固定して変化させた。また、Vecのbuilt-in関数であるsort関数の速度も合わせて計測した。
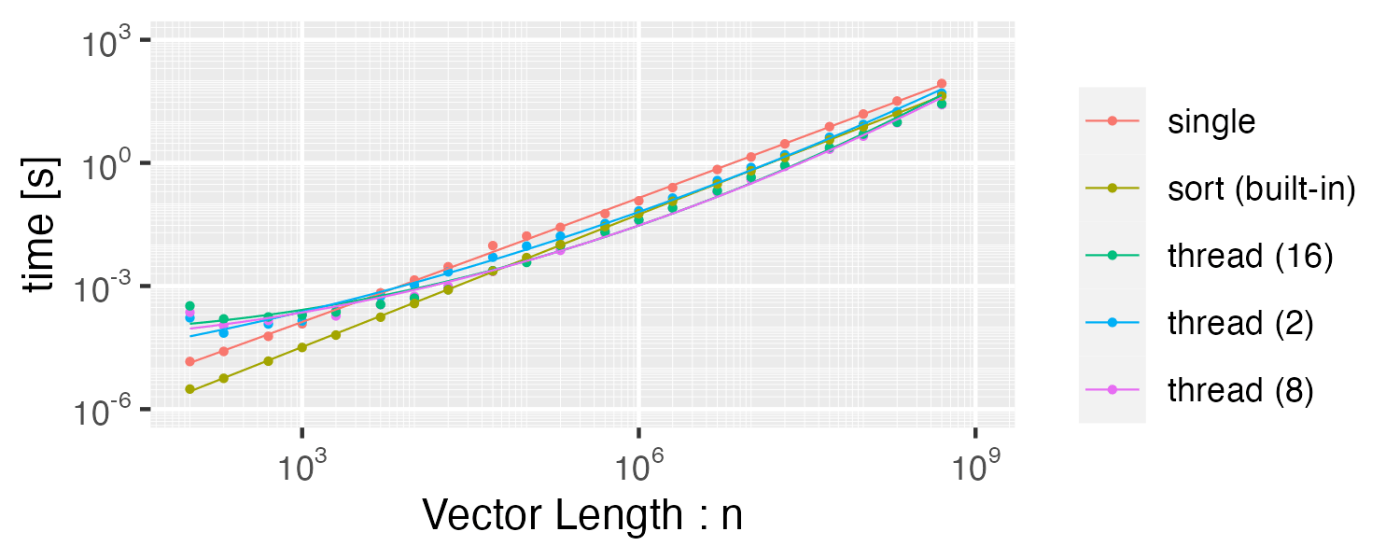
結論だけだと、「標準のsort関数は十分速いので、これを使っていれば大丈夫」であろうか。
以下のように、ドキュメントによるとマージソートではあるようだが、私が作ったコードより2-4倍速い。
The current algorithm is an adaptive, iterative merge sort inspired by timsort.
マルチスレッドの効果としては、コア数と同じ8スレッドが一番大きく、
最後u64 (8byte)にしたので、配列の容量としては 約3.7Gbyteの領域が必要。マージソートはマージするための領域が必要なので、2倍の領域が必要である。さらに、マルチスレッド版はsplit_offによりコピーを作っているので合計3倍が必要になる。これがだいたい11Gbyteになり、今回計測に使ったメモリが16Gbyteなので、実メモリが不足してしまっているのではないかと思われる。
Discussion