🎨
AHC048振り返り

2025/06/11に公開
 はじめにMC Digital プログラミングコンテスト(AtCoder Heuristic Contest 047)に参加した。順位は最終結果として400番前半。悪くはないのだが、トップの人とのスコアは１桁違う。

 問題問題を読んでどこから手をつければいいのかが悩ましい。貪欲に...と思っても何を貪欲にすればいいのか思いつかない。ベクトル演算で...と思ったがベクトルの長さ（絵の具を何gだすか）も考慮するとバリエーションが多すぎる。多項式として解けば答えは出せるかもだが、それを1gずつした取り出せない「操作」にマッピングするのが難しそうである。ターゲットの色はH = 1,000通りなので「残った」絵の具の活用が重要になることは予想できる。

結局、ランダムに操作をして良さそうな操作を選ぶという方法を実装してみることにした。結局最後までこれになったが。

 ランダムに操作する方法で解く
 パレットをどう表現するか？操作の中で難しいのが壁を壊したり作ったりすることで「ウェル」を結合したり分割したりする操作の処理。グリッド上での連結を表現するので、UnionFindを使いたい。しかしながらUnionFindは削除ができないので、簡単化する必要がある。具体的には、左か上のマスを最大1つ親に持つ木で管理することにした。こうすると木の「根」は必ず左上にあるので、結合・分割の処理は以下のようになる。
結合 : 根の左か上のマスとの間に枝を追加する
分割 : 枝を削除する


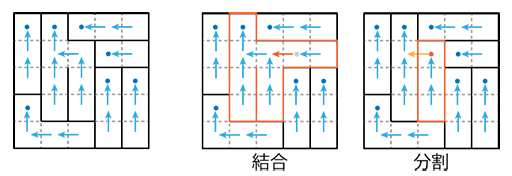
ウェルの管理方法と、結合, 分割
親が必ず1つなので、広い空間などは表現できないが、今回はウェルの大きさが問題なので制約にはならない。

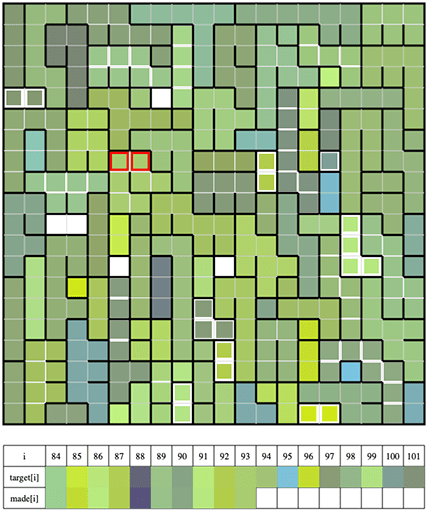
 とりあえずランダムに操作してみるランダムに操作していってちゃんと動くのか確認してみた。T回の操作でH個の色を作成しないといけないので、渡す操作分を引いたT/H - 1回適当に操作して、パレット上で一番必要となる色に近い色を渡すこととした。ただ、「絵の具の破棄」を少なく「絵の具の追加」を多く操作するように重みをつけた。


ランダムにひたすら操作している状態
やってみると、意外とうまくいっている印象。下の表で上の段が「必要となる色」下の段が「渡した色」なので、結構ちゃんと近い色を渡せていることが分かる。ちなみにseed = 0で 19,216,675点。低いのか高いのかはよくわからない。

 不要な操作を消していくひたすらランダムな操作をするだけでなんとかなりそうであったが、無駄も多い。上の図のように100色目あたりで、既にパレットは色だらけになっている。また、操作途中で似た色が出てきている場合もありそうだった。そこで、1色を渡すための処理を以下のようにした。

M回ランダムに操作する。この時途中のウェルの色もすべて保存しておく。
途中も含めてすべてのウェルで、必要となる色に最も近いウェルを探す。
そのウェルを作成するために必要な操作のみを抽出する。
上記 1 - 3を時間がある限り繰り返して最も良い操作を見つける
Mは定数にしているが、操作回数がTを超えないように残りの操作回数と定数の小さい方にした。とはいいつつ操作回数がTを超えそうなケースはなかった。パラメータの調整などを行って最終的には seed = 0 で 509,066点。スコアは低いほど良い。


ランダムに操作しつつ最も良い操作を残した場合

 分析
 絵の具の種類K
問題文をよく読むと必要となる色の決め方には特徴がある。全ての色を使って生成しているのだが、乱数のlogをとってから正規化して色を混ぜている。つまり、全部の絵の具を均等に混ぜるのではなく、特定の絵の具を極端に含む色となっている。
そこで、2つの絵の具を混ぜて、必要となる絵の具に最も近い色を求めてみた。なお、絵の具は 1〜4gのどられかを使うものとした。下図がその結果であるが、絵の具の種類Kが大きい時は、偏りも大きくなっておりそれなりの精度がでている。一方で、Kが小さい場合は、偏りはそこまで大きくなく、幅広い分布となっている。
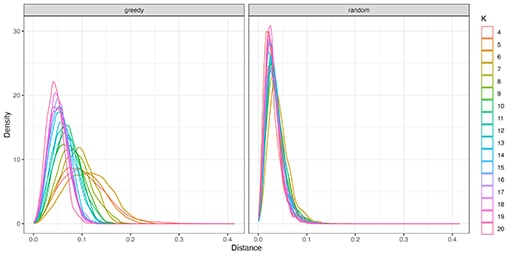
一方でランダムで操作した場合は、Kに関係なく距離（誤差）が小さい値となっているので、処理としては間違っていないように感じる。もしくは、貪欲法で解くには3個以上の絵の具の組み合わせを検討する必要があると考えられる。


2種類の絵の具を混ぜて必要な色を生成した時の距離（誤差）の分布

 絵の具を取り出すコストD
絵の具を取り出すコストDとスコアの関係をプロットしてみると、Dが大きい程スコアが高い（悪い）ことがわかった。スコアには絵の具を取り出すコストが含まれるためであるが、「必要となる色に最も近いウェル」を「最もスコアが低いウェル」に変更すると、スコアが下がってしまった。これは、Dが高い時、絵の具の中で一番近い色をウェルにだしてそれを渡してしまうのが最適となってしまうためであった。必要な色毎に最適化すると、前のフェーズで「残った」絵の具を活用できないためである。

最終的には、Dをそのままスコアに加えるのではなく、\alphaをかけて小さくすることで、コストの影響を考慮するようにした。


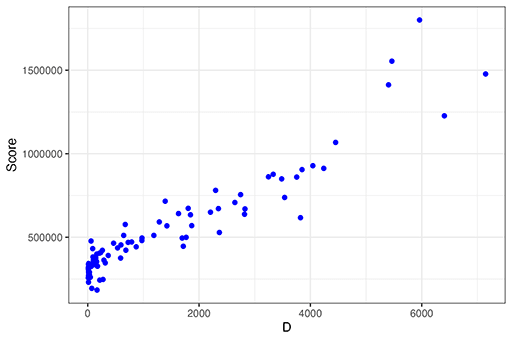
絵の具を取り出すコストとスコアの関係

 まとめ他の方の解説を読んでいると、やはり貪欲的に絵の具の組み合わせからもっともいいものを選んでいるようであった。ただ、今回は必要とされる色がすべての絵の具を混ぜて作成しているので、平均値に収束しがちなランダムな処理でもそこそこの点数がとれたのかな？とは思う。
ところで全然関係ないが、、「ウェル」って何だろう？というのが気になった。wellに「井戸」という意味もあって、そこから「くぼみ」という意味もある..らしい。