⚒️

焼きなまし法をグラフで見る

2024/06/09に公開

Python

AtCoder

焼きなまし

tech

はじめに

最適化問題の解法として有名な焼きなまし法 (Simulated Annealing) について、
atcoder の AHC002 Walking Tilesを対象とした、以下の記事で勉強した。原理は分かるのだけど、ランダムでうまくいくのがちょっと納得いかないので収束をグラフ化してみた。

Pythonでの実装

自分の理解を深めるために、上記の記事そのままでPythonで書き直してみた。基本的に繰り返し回数が効いてくるのでPythonは不利だと思うが、今回はそこまで問題なかった。記事に従って、深さ優先探索 (DFS, Depth-First Search), 山登り法 (Hill Climbing)，焼きなまし法（Simulated Annealing) とその拡張を実装した。Python固有の問題を以下に2つ示す。

再帰回数の上限

深さ優先探索は再帰で実装することが多いが、Pythonは関数の呼び出し回数に上限があるらしく、エラーがでてしまう。下記コードで再帰回数の上限を変更することができるが、今回は再帰を使わずにスタックで実装した。

import sys
sys.setrecursionlimit(2000)

expのover flow

指数関数を計算するmath.exp()は大きい数字（具体的には710以上）を入れるとOverflowErrorがでてしまう。焼きなまし法で、新しい解を採用するかどうかの判断に使うので、expに入れる前に値のチェックをして、大きい数値の場合は常に採用するようにすることで対応した。

各手法のスコアを見る

答えの収束

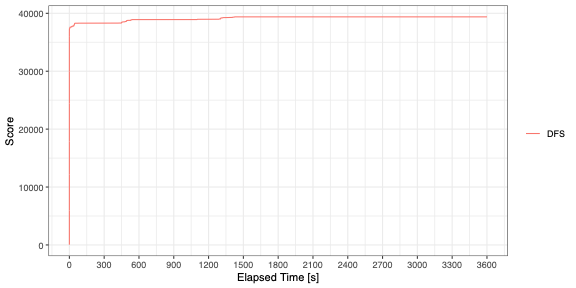
2.0秒間での制限時間の中でのスコアの推移をグラフ化した。深さ優先探索（DFS）は急激にスコアが上がっているがそこから伸びなくなっている。探索空間がかなり広いので、収束に時間がかかっている。ただ、探索空間の計算方法が思いつかないので、1時間回してみた。以下のグラフが示すように、スコアの上昇率はわずかであり、探索空間はかなり広いことが分かる。

山登り法 (Hill Climbing)，焼きなまし法（Simulated Annealing)は、0.05秒DFSで検索した結果を元にして探索を行った。そこからうまくスコアを上げている事が分かる。山登り法はそれでも局所解に入ってスコアが上がらなくなっている。焼きなまし法は、スコアが上下に揺れているが、局所解に入らずにうまく最適化できている。

最初のDFSの影響

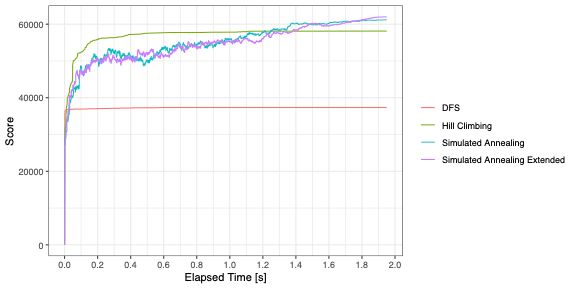
最初のDFSを途中で切り上げた時どうなるのか？を調べるため、DFSを1msで切り上げてみた。上のグラフをみると、わずかに低いスコアになっているが、ほぼ変わらないスコアをだしている。

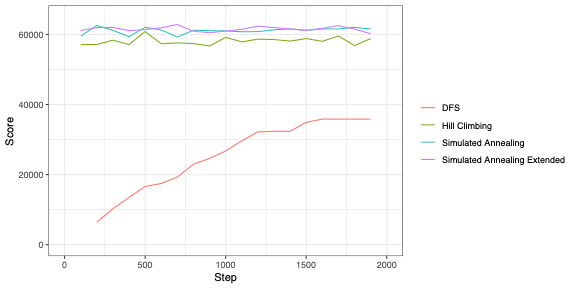
1ms以下の場合は、ステップ数でいった方が正確だと思うので、DFSを切り上げるステップ数を変更した時の各方法でのスコアをプロットした。1msでだいたい1000ステップ動いていた。DFSは切り上げた時のスコアを示しており、今回の実装はDFS部部に乱数的要素は入れていないので、すべての方式でこのスコアから始まっていると言える。現在のパスの一部を再計算する方式なので、最初のパスの長さが影響するかと思ったが、そこまで関係なさそうでだいたい同じようなスコアになっている。思っているよりもちゃんと収束する。

答えの安定性

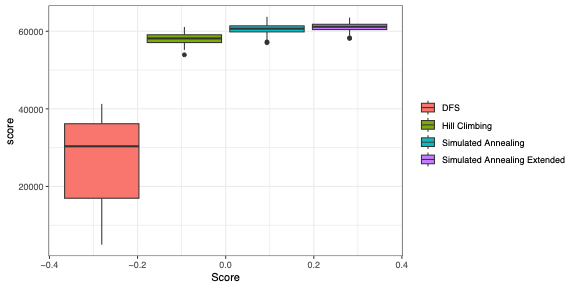
Seed 0の100問を使ってスコアの分布を導出した。DFSはかなりスコアにばらつきがあるが、山登り、さらには焼きなましは、どの問題にでも安定したスコアをだせていることがわかる。

深さ優先検索の可能性

深さ優先検索は、総当たりなので理論値がでてくるはずである。ただ、1時間動かしても答えがでてこなかったように、現実的には解けない。そこで別のアプローチがとれないか考えてみた。

枝切り

深さ優先探索や、幅優先探索で計算量が膨大になる時の対策としては、枝切りがよく知られている。解がない方向への探索をスキップする機能である。ただ、今回の問題の場合「明らかに解が存在しない」方向を判断するのは無理である。このため、ある一定ステップ以上、best scoreの更新がない場合は、そちらの方向に答えがないと判断するようにしてみた。以下、修正したコードの一部を示す。

else:
    cnt += 1
    if cnt > cnt_th:
        for _ in range(len(queue) - save_point):
            pp = queue.pop()
            if pp < 0:     
                pp = -pp - 1
                current_path.pop()
                visited[self.tile[pp]] = False
                current_score -= self.score[pp]
        cnt = 0
        cnt_th = (len(best_path) - len(current_path)) * 16
        continue

best scoreをだしたパスから、最もキューが短くなった箇所をsave_pointとして保存しておいて、そこまで戻ることにした。閾値としてはbest scoreをだしたパスとの差の16倍としている。ここらへんのパラメタは試行錯誤の結果である。

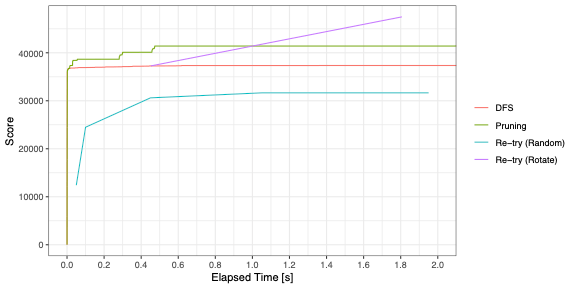
結果としては、少しは良い解を得ることができたが、焼きなまし法どころか山登り法にも勝てていない。
枝切りのやりすぎっぽく、5秒ぐらいで探索が終わってしまうが、同じようなスコアしかだせていない。

やり直し

DFSのグラフをみると収束がかなり速いので、探索時間を短くしてしまえばいいのではないか？と考えた。50ms探索したら切り替えて、最初から探索をやりなおす。探索の方向を毎回ランダムにしてしまえば、毎回違うパスを検索するので、最適解が見つかる可能性がある。結果は前のグラフのRe-try (Random)であるが、かなり低い結果となった。今回はパスの長さを確保することが重要であるため、探索の方向の順番が決まっていた方が長いパスを検索しやすいためであると考える。

であれば、1回目は左→右→上→下の順で探索したが、2回目は右→上→下→左の順で探索するようにしてみた。この場合4通りしかないので、0.5秒ずつそれぞれの順番で探索する。Re-try (Rotate)がそのグラフであり、一番高いスコアはだしているが、山登り法にも劣っている。

おわりに

焼きなまし法について、その動きをグラフで見てみた。ランダムに切ったり貼ったりしてうまくいくのか？と懐疑的であったが、問題の設定方法にもよるのだろうが、うまくいくことが分かった。スケールが大きい時はアルゴリズムとして悪くないと感じた。