スライド最小値・最大値アルゴリズム from ABC352

アルゴリズム力強化のため、AtCoderに初参加してきました。D問題(ABC352)で敢え無く撃沈。
目下の第一目標を「D問題レベルをコンスタントに解けるようになること」に定め、備忘のため、毎週のAtCoder参加＋学習したアルゴリズムを記録しておきます。

アルゴリズムの正確な解説は保証しておらず、自分の理解に落とし込んだ上で、なるべく分かりやすくアウトプットすることを目的としておりますので、そこはご了承ください。
その前提で誤り等についてはコメントで指摘頂けると非常に助かります。

When to use

配列$P = (P_1, P_2, ..., P_N)$に対して、長さkの部分列$P_i, ..., P_{i+k}(1\leqq k \leqq N)$の区間最小値・最大値を求める

Time Complexity

$O(N)$

ループによる愚直な実装は$O(NK)$、セグメント木等を使うことで$(NlogN)$となる
ABC352のD問題の制約は$1≤K≤N≤2×10^5$のため、ループ実装ではTLEとなる

How to implement

Deque（先頭・末尾の両方向から値の挿入・取り出しが可能なデータ構造）を使うことで、$O(N)$での実装が可能になる。

実際にABC352 D - Permutation Subsequenceを考える。まず問題を注意深く読むと、各$a$について、$i_K - i_1$というのは最大のindexと最小のindexの差分に相当することが分かる。

具体例を挙げると、10 1 6 8 7 2 5 9 3 4($N=10$, $K=5$)というインプットがあった際に、良い添字列は$a$を1つずつずらして下記のように考えることができる。

• $a=1$について、 $\{P_1, P_5, P_6, P_8, P_9\} = \{1, 2, 3, 4, 5\}$、よって$i_K - i_1 = 8$
• $a=2$について、 $\{P_2, P_5, P_6, P_8, P_9\} = \{2, 3, 4, 5, 6\}$、よって$i_K - i_1 = 7$
  ...

このことから、下図のように$(1, 2, 3, ..., N)$に相当するindex番号を格納した配列Qを考えることで、スライド最小値（最大値）の問題に落とし込むことができる。

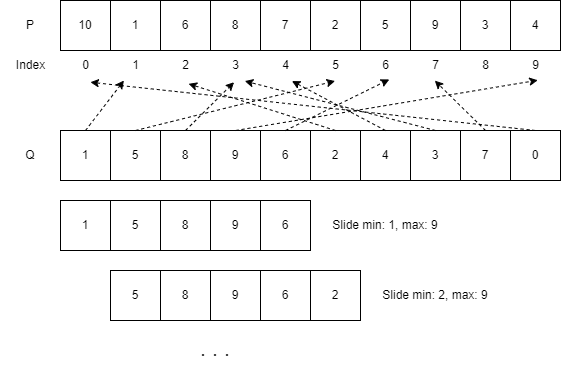
Dequeを使ってスライド最小値を求める場合、下記のようにQueueを更新することで各区間最小値を取得することができる。

• DequeにはQのindexを保持する
• Dequeは常にindexに対応するQの値が単調増加するように、要素を追加・削除する

つまり、C++の実装としては下記のようになる。

/**
 * @brief Sliding window minimum algorithm
 * @param[in] target Original array to calculate sliding minimum values
 * @param[out] window_size Sliding window size
 * @return Minimum values for each sliding window
 */
std::vector<int> CalculateSlideMinValues(const std::vector<int>& target, const int window_size) {
  std::vector<int> ans{};
  std::deque<int> deq{};

  const int array_size = static_cast<int>(target.size());
  for (int i = 0; i < array_size; ++i) {
    // Remove elements if new value is smaller than last element of deque
    while (!deq.empty() && target[deq.back()] >= target[i]) {
      deq.pop_back();
    }
    deq.push_back(i);

    if (i - window_size + 1 >= 0) {
      ans.push_back(target[deq.front()]);
      // Remove elements out of slide window
      if (deq.front() == i - window_size + 1) {
        deq.pop_front();
      }
    }
  }
  return ans;
}

Dequeの追加・削除の回数が$O(N)$となるので、アルゴリズムの計算量は$O(N)$となる。

スライド最大値については、上記の関数についてQの値が単調減少するようにDequeを更新することで実装できる。もしくは、オリジナルの配列の符号を反転させることでスライド最小値の問題へと帰着させることができる。

  const auto min_values = CalculateSlideMinValues(q, k);
  const auto max_values_sign_reversed = CalculateSlideMinValues(q_sign_reversed, k);

感想

一つ一つのアルゴリズムを丁寧に学び、理解を深めることで、問題に対するアプローチを増やすことが大事だと感じました。