【Coursera】Introduction to Self-Driving Cars: Week4
Courseraのトロント大学が提供している専門講座Self-Driving CarsのIntroduction to Self-Driving Carsコースのメモ
Week3はこちら
Lesson 1: Kinematic Modeling in 2D
Kinematic(運動学)とDynamic(動力学)
車両の動きは、動きを定義する幾何学的制約を考慮する(kinematic)か、車両に作用する全ての力とモーメントを考慮する(Dynamic)ことでモデル化できる。
- Kinematicモデリング
- 加速が著しくない低速では車両の動きを捉えられる。
- Dynamicモデリング
- 車両の動作範囲全体を通して動作予測に優れているが、Kinematicに比べ開発に多くの関与が必要になる。
座標フレーム
- グローバルワールド、慣性座標フレーム
- 地球に紐付く固定参照フレームで主にEast North Up(ENU、近くの基準点に相対的)、Earth-Centered Earth Fixed(ECEF、GNSSで使用)として表される。
- ボディフレーム
- 車両の重心や後車軸の中心点など重要な位置に配置され、固定された慣性フレームに対して、動いたり回転したりする。
- センサーフレーム
- 各センサーの出力に使用される座標
多くのロボティクスではいくつかの座標を移動するシステムに紐付け、これらのフレームから慣性フレームの要素を表現する。これを行うにはある座標から別の座標への変数の変換が必要になる(ボディフレームから慣性フレームへなど)。
一つのセンサーを使用した二輪ロボットでは3つのフレームの考慮が必要になり、自動運転車では何十個にもなる。
2D kinematic modeling

非ホロノミック制約を使用してロボットのkinematicモデルを定義する。
ロボットの速度はそのパスへの接ベクトルで定義される。ロボットの方向角をθとすると
二輪ロボットkinematic model

このモデルの入力は

両方の車輪の速度が同じであればロボットは直線的に動き、異なる場合はICR(瞬間回転角)でカーブする経路をとる(下図の

連続時間方程式を離散化することでモデルを微分形式から有限差分形式へ変換できる(シミュレーションに使える)。
Lesson 2: The Kinematic Bicycle Model
Kinematic bicycle model(自転車モデル)は古典的なモデルでシンプル(単純化した車両モデル)、車の非ホロノミック制約に忠実であることから、通常の運転状況下で車両の動きを驚くほどうまく捉える。
二輪ロボットでの例に加え、モデルは前輪操舵で慣性フレームFIで示される2D平面で動作すると仮定。
自転車モデルのkinematicを分析にするには車両上の基準点(X, Y)を選択する。基準点は後車軸の中心、前車軸の中心、または車両の重心など。選択する基準点でkinematic方程式が変わり、コントローラーの設計が変わる。
二輪ロボットkinematic model
後車軸の中心を基準点とする場合

-
θ -
L
自転車モデルへの入力は
-
δ -
v
スリップなし状態を仮定しており、横方向への移動や縦方向スリップは考えない。したがって、車輪の回転速度に基づいて前進速度の計算が可能。
スリップなしのため、自転車の回転率
整理すると

前車軸の中心を基準点とする場合
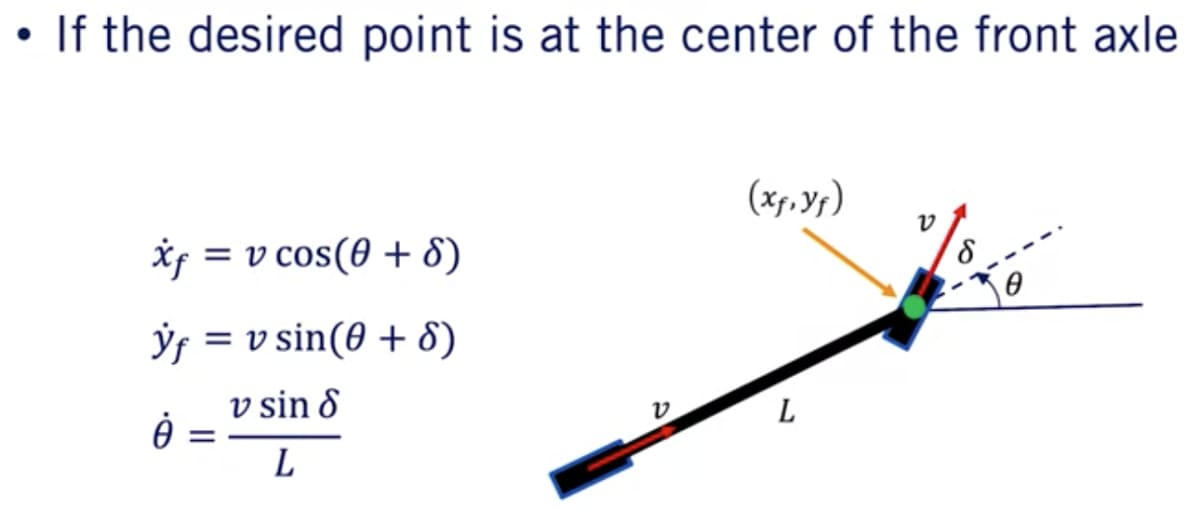
車両の重心を基準点とする場合

後車軸、前車軸の場合と異なり、サイドスリップ角
最後にこのkinematic modelは入力として速度
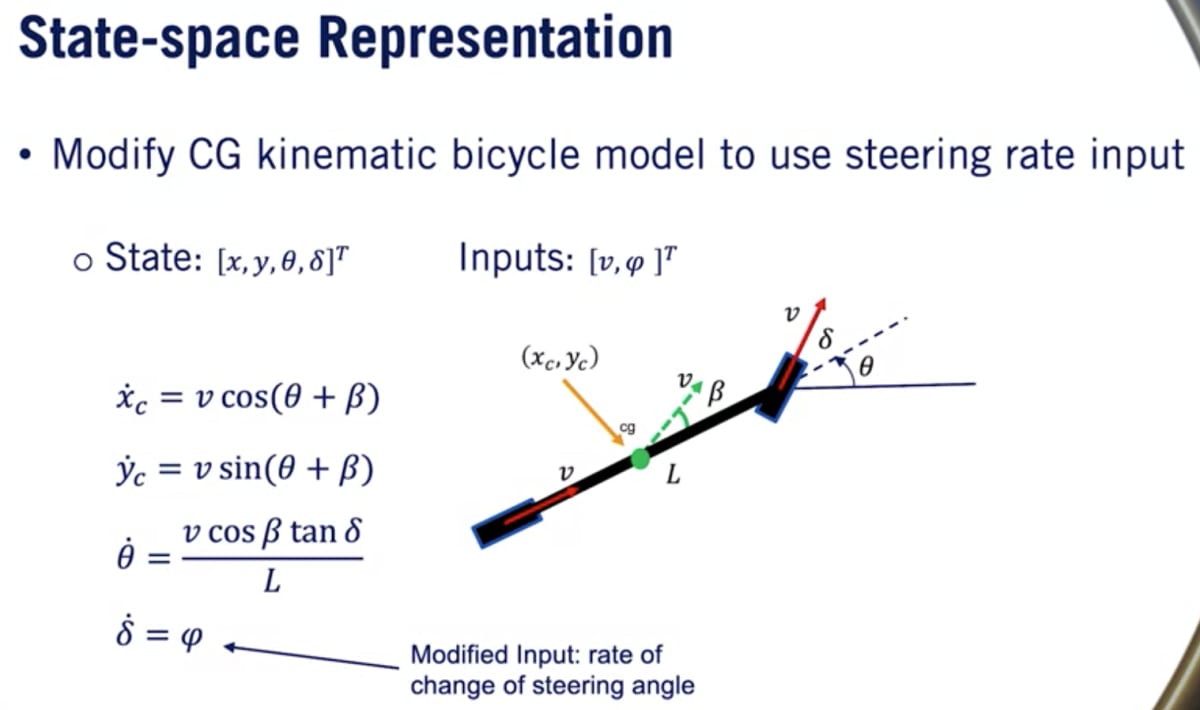
Lesson 3: Dynamic Modeling in 2D
なぜDynamicモデルが必要か?
スピードが高速、滑りやすい道路ではスリップなしの条件が成立しなくなる(車両にかかる力がタイヤを舗装上で滑らせるため)。スリップ状態での力のバランスをモデル化すると運動の正確な予測ができるようになる。
また車内の多くのサブシステムにはハードなKinematic制約がそのサブシステムの変遷を正しく補足しない同様の条件があるため、Dynamicモデルが必要になる。
- ドライブトレインの例:エンジンとトランスミッションシステムを介してスロットル位置から車輪トルクへの結合を確保するためにトルクのバランスが必要になる。車両に作用するモーメントの力のバランスを明示的にモデル化することで車両が受ける加速度を決定し、それらを使用して車両の運動をモデル化できる。
Dynamicモデリングプロセスの定義
- モデルで使用する座標フレームの設定(ボディフレーム、慣性フレームなど)。
- DynamicシステムをDynamic要素の塊ごとに分解、それぞれのモデルを定義する。
- 各要素群の剛体に対するフリーボディダイヤグラムを描き、ボディーに作用する全ての力とモーメントを適切に名前付けしてモデル化する。
- ニュートンの第二法則を使用して、Dynamicモデルを定義する数学方程式を記述し、並進Dynamicsの各軸に沿ったすべての力と回転Dynamicsの各回転軸のすべてのモーメントを合計する。
結果は剛体の運動を記述する常微分方程式でこれがDynamicモデルになる。
- ショックアブソーバーの例
- 車輪の例
車両の場合はとても複雑なモデルとなる。
Lesson 4: Longitudinal Vehicle Modeling
縦方向の車両Dynamicモデルは前方運動を生成する車両のDynamicsに基づく。

-
F_{xf}, F_{xr} -
F_{aero} -
R_{xf}, R_{xr} -
mg\sin a a \sin a=a
これらの力の間の不均衡が縦方向の車両の加速度を表す。

-
F_{aero} c_{a} -
R_{xf}, R_{xr}
これらは単純化しているが、実際に使用されるモデルの忠実度はコントローラー、シミュレーション環境に必要な精度に依存する。

前輪・後輪に作用する力は、パワートレインと一連のコンポーネントからの生成(エンジン、バッテリーから車輪まで)としてモデル化できる。コンポーネントにはトルクコンバータ(クラッチ)、トランスミッション(ギヤボックス)、デファレンシャルなどが含まれる。
- ギヤが入るとエンジンと車輪が接続され車輪速度とエンジン速度の関係をKinematic制約としてモデル化できる。車輪の回転速度ωはいくつかのギヤ比(
GR GR ω_{t} GRω_{t}=GR ω_{e} - 車両の前進速度は車輪の角速度にタイヤの有効半径をかけた値にも比例する。ほとんどが固定タイヤ半径としてモデル化されるが、車の力とモーメントに起因するタイヤの予測できる変形を考慮してより忠実どの高いモデルにもできる。車両の前進速度は固定タイヤとすると有効なタイヤ半径と車輪速度の掛け算になる。
各コンポーネントのDynamicモデル

- Wheel: パワートレイン側からのトルクと外部抵抗力からのトルクが交差する場所。
F_{x} T_{wheel} - Transmission:
T_{wheel} T_{t} ω_{t} T_{t} - Torque Converter: 実際はトルクコンバータは複雑なDynamicsを持っている(エンジンの結合・分離を可能にする軸受、インペラを通過する流体など)。エンジンと結合するとエンジン速度とほぼ同じと想定できる。
- Engine: エンジンのトルクはエンジンから生成したトルクからトルクコンバータからのタービントルクを引いたものに等しい。
Lesson 5: Lateral Dynamics of Bicycle Model
このレッスンでの仮定
- 前方への縦方向速度は一定(横方向のDynamicモデルと分けるため。モデリングを簡素化できる一方でカーブから加速、減速する際にモデリングが不正確になる)
- Kinematic自転車モデルと同様に前輪・後輪の左右の車輪を一つにまとめる。
- サスペンションの動き、道路の傾斜、空力など他の非線形効果は無視する(実際は、これらは車輪の力に大きな影響を与えることがある)。

- 車両の重心をDynamicモデルの基準点として使用する。
- 横方向の加速度(慣性フレームの合計加速度)
a_{y} \overset{{..}}y ω^{2}R V\overset{{.}}β V\overset{{.}}ψ -
\overset{{.}}β \overset{{.}}ψ m V
車両のDynamicsモデリングの重要なコンポーネントの一つはタイヤで一般にタイヤの力を正確に予測することは難しく、タイヤモデルは非線形で経験的に特定される傾向がある。
通常の運転下では単純な線形近似を使用してタイヤの力の生成をモデル化できる。この近似は小さなスリップ角(一般に8度未満)に対してのみ有効でタイヤの力は特にスリップ角に応じて線形変化するものとしてモデル化される。
コーナリング剛性(

この導出に使われた仮定と近似によって横方向のDynamicモデルは線形となる。
この状態空間表現は横方向制御用のPICやMPCなどのさまざまな制御戦略を設計するときに役に立つ。このモデルの線形性はカルマンフィルターを使用した状態推定にも使われる。

Lesson 6: Vehicle Actuation
横方向の入力はステアリング角度、縦方向の入力はスロットリングペダルの位置とブレーキペダルの位置でこれらが車両に作用する力とモーメントの一部を定義し、車両の状態を支配する常微分方程式の入力になる。
縦方向と横方向は互いに影響し合うことがあるが、ここでは切り離して考える。
車両制御の主なタスクは適切なステアリング、スロットル、ブレーキのコマンドを提供して車両の望ましい経路を保ち、目的の速度プロファイルを維持すること。これらの必要な要素はモーションプランニングシステムによって提供されると想定する。
ステアリング
ステアリング角度は特別なメカニズムとギア比によって車輪角に変換され、車両が曲線状の経路に沿うための横方向の力を提供する。
最も単純なモデルでは車輪角
スロットリング
スロットリングペダルの位置はエンジンやモーターから生成されるトルクを駆動する。このトルクはトランスミッションシステムに渡され、ギヤボックスが動作モードに必要な速度に基づいてギヤを変更する(ギヤ1, 2はトルクモードで高いギヤは速度モードと呼ばれ、トルクコンバータの動作モードを示す)。最後にデファレンシャルを介して車輪に動力が流れ牽引力を生み出す車輪のトルクが生成される。牽引力は空力や路面摩擦などの抵抗力よりも大きくなければならない。
ドライバーはスロットリングペダルから車両の加速に必要なトルクを要求できるが、レスポンスは動力生成装置(ガソリンエンジン、ディーゼルエンジン、電気モーターなど)によって異なる。
- ガソリンエンジンの最高トルクの動作点は通常2000-3000RPMで低速、高速ではトルク生成能力が低下する。
- ディーゼルエンジンは幅広い範囲で安定したトルクを生成するので大型車に適する。
- 電気モーターは1500などの低いRPMで効率的。
トルクとRPMの関係は二次多項式として表せられる。

-
T_{e} -
x_{θ} -
ω_{e} -
A_{0}, A_{1}, A_{2}
このモデルは半経験的モデルと呼ばれ、より詳細なモデルには流体、熱伝達、燃焼など他の多くの現象を含めることができる。
エンジンの速度とスロットリング位置が与えられるとこの半経験的モデルに基づいて生成されるトルクを計算し、車両の縦方向のDynamicsモデルの入力にできる。
ブレーキ
ブレーキはドライバーが指示したブレーキ位置から始まり、電子制御ユニットによってブレーキ圧力に変換される。ブレーキ圧力によってブレーキディスク、またはドラムにブレーキ力が生じ、車輪にて車輪ブレーキトルクになる。車輪ブレーキトルクは車両を減速させるため負の縦方向の力を生み出す。
制御ユニットがブレーキトルクを管理しているため、ブレーキシステムのレスポンスはかなり予測可能。ここでは詳細にモデリングはせずにペダル位置からブレーキトルクへの単純な線形マッピングを使用する(
単純化したもののブレーキングシステムは車両制御に不可欠であり、ハードブレーキ、アンチロックブレーキなどの機能は車両の安全性や性能を大幅に向上させた。
Lesson 7: Tire Slip and Modeling
タイヤは車両と道路の間のインタフェースであり、これまでのアクチュエーションモデルはタイヤモデルへの入力となる。Dynamicsモデルに基づいてコントローラを開発するには両方のDynamicsを理解する必要がある。
スリップ角
車両のスリップ角は車両の実際の運動方向と車両の前方の向きとの間の角度。
- 車両のスリップ角βは横方向速度
V_{y} V_{x} - スリップ角が小さい場合は横方向速度
V_{y} V_{x}
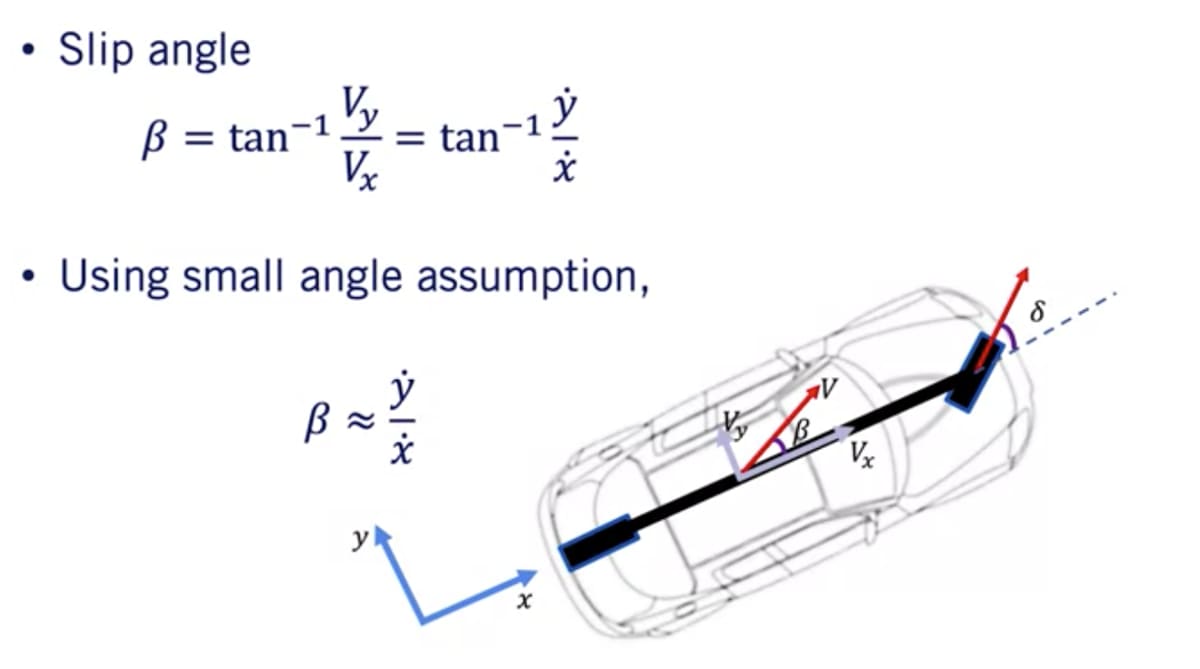
タイヤのスリップ角

スリップ率(縦スリップ)
タイヤの変形とそれに作用する縦方向の力との関係を示す。
加速、ブレーキの際にタイヤで観測された角速度は、タイヤと道路との間にスリップがあるため、純粋な回転運動として期待される速度とは一致しない。
タイヤの回転速度と車両の縦方向の速度の差は純粋な回転速度に対する比率として表すことができ、これをスリップ率と呼ぶ。
車両の速度とタイヤの角速度の違いには3つのケースが考えられる。
- 車両の速度の方が速い場合: 車輪は横滑りしている。車両の減速中に発生する。
- タイヤ速度の方が速い場合: 車輪はスピンしている。凍結路面やドリフト中に起きる。
- タイヤ速度は0で車両速度が0でない場合: 車輪はロックしている。停止性能の低下、ステアリング制御の喪失が起きるため、ABSはこれを回避しようとする。

タイヤモデルの入出力

代表的なタイヤモデル
- 分析モデル
- 物理学に基づいたモデル
- シンプルかつ高速だがタイヤの全ての動作範囲で十分な性能を発揮するものではない。
- Brush, Fialaモデルなど
- 数値モデル
- シミュレーションベース
- 分析モデルより正確だがモデルベースの制御開発に使用するのは困難
- パラメータ化モデル
- 広範な測定データによってパラメータ化された関数で定義するモデル
- タイヤごとにパラメータを求める必要がある
- 予測の正確さと計算時間とのバランスが良いので広く使われる。
- Linear, Pacejka, Dugoffモデルなど
パラメータ化モデル
Linearタイヤモデル
- タイヤの縦方向、横方向の力を力係数
C - 線形領域のかなりの部分で適切な近似だが飽和領域に入ると精度が低下する。
- 代表的な自動運転の場合、タイヤはほぼ線形領域で動作するため、線形モデルは近似値として適切。

Pacejkaタイヤモデル
- モデルベースの制御で最も重要かつ広く使用されているモデルの一つ。
- 縦方向のタイヤ力はスリップ率、タイヤ垂直抗力、路面摩擦係数の関数。
- 実験から
B, C, D, E

縦方向ではスリップ率が大きくなると線形モデルの近似精度が低くなる。またデータはモデルよりも拡散しており、タイヤの力のモデリングの難しさをよく表している。
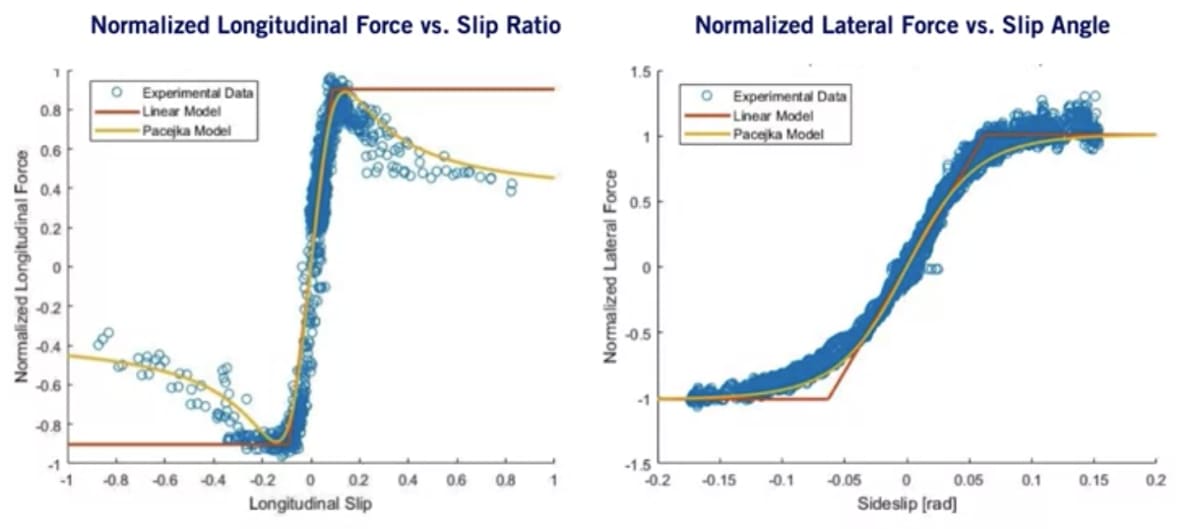
Week4はこれにて終了。
Week5はこちら
Discussion