SECCON CTF 13 Quals 脆弱Writeup
SECCON CTF 13 予選をチーム「full_weak_engineer | Please subscribe! -> https://asusn.online」で参加しました。
国内10位という結果でした。
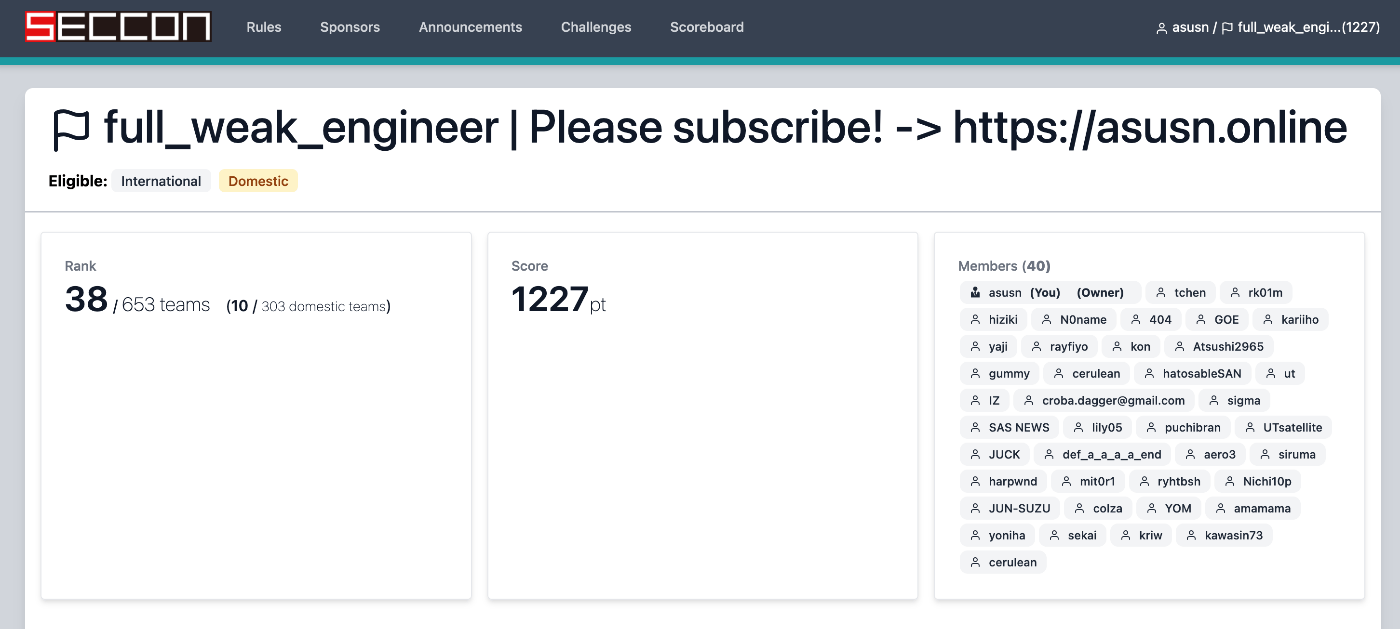
今年は、国内の上位8チームが決勝に進出できるのですが、あと1チーム差で惜しくも決勝進出ならずでした。(国内トップチームが国際決勝進出のため国内9位までが決勝進出)
悔しいです。
大会終了後「来年強くなってまた会おうな✋」と漫画みたいな解散をしました。
チームメンバーのWriteup
dual_summon (123pt, 63 Solved)
自分が解けた問題について、解法を書いていきます。
20時間ほどこの問題に費やして、大会終了まで1時間を切った13:10にflagを提出できしました。
諦めずに取り組んでよかったです。
作問者のkurenaifさんがwriteup streamで「GCM初めての人でも頑張れば大会中に解けるレベル」と言っていましたが、本当にその通りなんですがギリギリでした(笑)
問題
問題は至ってシンプルでした。
AESのGCMモードにおいて、keyが異なり、nanceは一致している場合に、認証用のタグを一致させる平文を送ることはできるか?という問題です。
from Crypto.Cipher import AES
import secrets
import os
import signal
signal.alarm(300)
flag = os.getenv('flag', "SECCON{sample}")
keys = [secrets.token_bytes(16) for _ in range(2)]
nonce = secrets.token_bytes(16)
def summon(number, plaintext):
assert len(plaintext) == 16
aes = AES.new(key=keys[number-1], mode=AES.MODE_GCM, nonce=nonce)
ct, tag = aes.encrypt_and_digest(plaintext)
return ct, tag
# When you can exec dual_summon, you will win
def dual_summon(plaintext):
assert len(plaintext) == 16
aes1 = AES.new(key=keys[0], mode=AES.MODE_GCM, nonce=nonce)
aes2 = AES.new(key=keys[1], mode=AES.MODE_GCM, nonce=nonce)
ct1, tag1 = aes1.encrypt_and_digest(plaintext)
ct2, tag2 = aes2.encrypt_and_digest(plaintext)
# When using dual_summon you have to match tags
assert tag1 == tag2
print("Welcome to summoning circle. Can you dual summon?")
for _ in range(10):
mode = int(input("[1] summon, [2] dual summon >"))
if mode == 1:
number = int(input("summon number (1 or 2) >"))
name = bytes.fromhex(input("name of sacrifice (hex) >"))
ct, tag = summon(number, name)
print(f"monster name = [---filtered---]")
print(f"tag(hex) = {tag.hex()}")
if mode == 2:
name = bytes.fromhex(input("name of sacrifice (hex) >"))
dual_summon(name)
print("Wow! you could exec dual_summon! you are master of summoner!")
print(flag)
解法に至るまでの過程
AESのGCMモードは初めましてだったので、そこを調べるところから始まります。
英語のWikipediaを読むところからです。(英語版なの大事。情報量が違います。画像もivが無かったりと微妙に違いました)
調査
「AES GCM CTF」などで検索して出てきたwriteupなどを漁っていましたが、タグを一致させるようなものは見つからず。
作問者のkurenaifさんのGCMについての解説問題も出てきました。
これを見ることで、GCMについての理解度が高まりました。
動画の概要欄にはフルスクラッチの実装が貼られていて、これを動かしてみました。
動かしてみる
このフルスクラッチを動かしながら、内部のパラメータを覗いてみることで、理解度が爆上がりしました。
実装を見てもよくわからない部分は、GCMの論文とにらめっこしました。
おかげで、ACM-GCMこの図の意味が完全に理解できました。(Hの多項式が具体的にどのような値かなど)

今回は1ブロックのみなので、もっとシンプルな図で表すことができます。
Auth Dataも指定がないので、省略できました。

ここまで理解しても、異なるkeyでタグを一致させる平文を求めるのは無理だろ!!!とずっと悩んでいました。
途中、いろいろいじっていたら、タグから平文を逆算できるようになりました。
とてなのよ〜。(シシガシラ風に)
今回の問題を解くには全く役に立たないのですが、こうやってCTFの他の問題って生まれていくんでしょうね。ストックしておきます。
着想
ここまでの理解度を持って、もう一度調べ上げた記事を読み漁っていると、やっぱりこれ近くね?というCTFの問題が見つかります。
この問題は、好きな入力に対する暗号とタグのペアを知れるときに、特定の暗号に対するタグを作れという問題でした。
2組の暗号とタグが分かれば、Hなどのパラメータが求められるというものでした。
こういうのをForbidden Attackと呼ぶらしいです。
1周目の調査ではさっぱりわからなかった数式も、理解度を高めた上での2周目になると「読める!!読めるぞ!!」状態になりました。
Key1とKey2それぞれで、Hを求めたあとに、タグと平文を1つの変数にして、連立方程式を解けばいけるのでは???という発想になりました。
(実際、立式するのにかなり時間がかかりました。)
解法
Hを求める
まずは、Keyを1つに固定して考える。
暗号
(
これを平文
ここで、2つの平文
両辺足す。(加算はXORとなる)
これを解けば
Key1に対する
タグと平文の連立方程式を解く
求めたい平文を
これを
ここで、
実は、これは求めることができる。(コードのコメントで該当箇所を記述する)
よって、これがタグを一致させる平文となる。
Solver
根幹となるコードは以下の通り。
コードの一部はこちらのwriteupから拝借した。
#!/usr/bin/env sage
from sage.all import *
from Crypto.Util.number import long_to_bytes as lb
from Crypto.Util.number import bytes_to_long as bl
from binascii import unhexlify, hexlify
from sage.all import *
import struct
def bytes_to_polynomial(block, a):
poly = 0
# pad to 128
bin_block = bin(bl(block))[2 :].zfill(128)
# reverse it to count correctly, wrong don't reverse it lol
# bin_block = bin_block[::-1]
for i in range(len(bin_block)):
poly += a^i * int(bin_block[i])
return poly
def polynomial_to_bytes(poly):
return lb(int(bin(poly.to_integer())[2:].zfill(128)[::-1], 2))
def convert_to_blocks(ciphertext):
return [ciphertext[i:i + 16] for i in range(0 , len(ciphertext), 16)]
def xor(s1, s2):
if(len(s1) == 1 and len(s1) == 1):
return bytes([ord(s1) ^^ ord(s2)])
else:
return bytes(x ^^ y for x, y in zip(s1, s2))
F, a = GF(2^128, name="a", modulus=x^128 + x^7 + x^2 + x + 1).objgen()
R, x = PolynomialRing(F, name="x").objgen()
# Key1の平文とタグ
P1_1 = b'0000000000000000'
T1_1 = bytes.fromhex('b4a62b2a590d64c24e739fcc21063396')
P1_2 = b'1111111111111111'
T1_2 = bytes.fromhex('4a437f6da2f84bcea8fda42b2608c458')
# Key2の平文とタグ
P2_1 = b'2222222222222222'
T2_1 = bytes.fromhex('05a6507f3cc4d284b091f5f5b0de4692')
P2_2 = b'3333333333333333'
T2_2 = bytes.fromhex('1696769e2e30b30f9d88faba59cf4911')
# Key1についてのパラメータを求める
P1_1_p = bytes_to_polynomial(P1_1, a)
P1_2_p = bytes_to_polynomial(P1_2, a)
T1_1_p = bytes_to_polynomial(T1_1, a)
T1_2_p = bytes_to_polynomial(T1_2, a)
L = struct.pack(">QQ", 0 * 8, 1 * 8)
L_p = bytes_to_polynomial(L, a)
G_1 = (P1_1_p * x^2) + (L_p * x) + T1_1_p
G_2 = (P1_2_p * x^2) + (L_p * x) + T1_2_p
P1 = G_1 + G_2
H1 = P1.roots()[0][0]
S1 = G_1(H1) # S'_1 = E_{1k_1} H_1^2 + E_{1k_0} の値
# Key2についてのパラメータを求める
P2_1_p = bytes_to_polynomial(P2_1, a)
P2_2_p = bytes_to_polynomial(P2_2, a)
T2_1_p = bytes_to_polynomial(T2_1, a)
T2_2_p = bytes_to_polynomial(T2_2, a)
F_1 = (P2_1_p * x^2) + (L_p * x) + T2_1_p
F_2 = (P2_2_p * x^2) + (L_p * x) + T2_2_p
P2 = F_1 + F_2
H2 = P2.roots()[0][0]
S2 = F_1(H2) # S'_2 = E_{2k_1} H_2^2 + E_{2k_0} の値
# タグが一致する平文を求める
plaintext_with_same_tag_p = (L_p * (H2 + H1) + (S2 + S1)) / (H2^2 + H1^2)
plaintext_with_same_tag = polynomial_to_bytes(plaintext_with_same_tag_p)
print(f'{plaintext_with_same_tag = }')
問題のサーバに接続して、Key1に対するパラメータを推定するために、「0000000000000000」と「1111111111111111」のタグを取得する。
同様に、Key2でも「2222222222222222」「3333333333333333」のタグを取得する。
これらの値からタグが一致する平文を計算して、それをサーバに送ってあげればflagゲット!
SECCON{Congratulation!_you are_master_of_summonor!_you_can_summon_2_monsters_in_one_turn}
おわりに
来年強くなってまた会おう✋
チーム「脆弱エンジニア(full_weak_engineer)」では、SECCON CTF決勝進出を目指してCTFに取り組んでいます。
チームでCTFをやりたいメンバーを常に募集していますので、YouTubeの概要欄にあるDiscordリンクから、気軽にご参加ください!
Discussion