不偏分散で N-1 で割る理由 を自力で導出する

はじめに【標本分散と不偏分散】

分散は、標本データ算出する方法と母集団から得る方法の２種類があります。
前者を標本分散$s^2$、後者を母分散$\sigma^2$と呼びます。

標本分散$s^2$は、サンプルサイズ$N$で母集団からサンプリングした標本$X$（サンプルデータ）から算出された分散の値であり、母集団全体の母分散$\sigma^2$とは、サンプリング時の偏りなどの影響により一致しません。
これは、母平均$\mu$と標本平均$\bar{X}$も同様で、一致しません。

だからこそ、統計学では、標本平均$\bar{X}$や標本分散$s^2$などから、母平均$\mu$や母分散$\sigma^2$を推定する手法がさまざま提案されています。

しかしながら、数ある統計学の書籍などを見ると、標本分散$s^2$ではなく、不偏分散$u^2$を利用することを求められます。

この不偏分散$u^2$の定義が、下記のように奇妙な定義になっています。

$$u^2 = \frac{1}{N−1} \sum_{i=1}^{N} (X_i - \bar{X})^2$$

標本分散$s^2$では、標本平均$\bar{X}$からの２乗距離を、サンプルサイズ$N$で割っていますが、不偏分散$u^2$では、$N-1$で割っています。

書籍やWeb記事などでは、「標本分散$s^2$は、母平均$\mu$ではなく、標本平均$\bar{X}$との距離から計算されているため、実際の母分散$\sigma^2$よりも、過小評価されている。だからそれを補正するために、少し小さい$N-1$で割り算します」といった解説をよく目にします。

これは実際その通りで、標本$X$から算出された標本平均$\bar{X}$は、サンプリング時の偏りを反映した値になっているため、その標本平均$\bar{X}$からの距離は、母平均$\mu$からの距離よりも必ず小さくなってしまうというのは、感覚的にも理解できます。

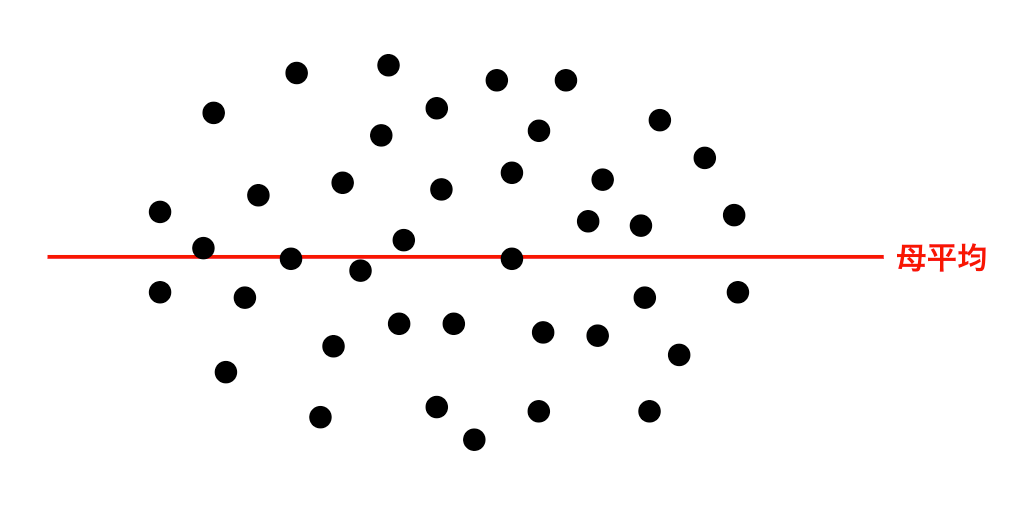
例えば下記の図をご覧ください。

下記はある集団のすべての標本を可視化した図になっています。
ある集団のすべての標本を、黒点で表示しているため、縦の軸に注目すると、高さ的にちょうど、ど真ん中が母平均$\mu$になります。

一方で、この母集団から、10点サンプリングした点を青点で下の図に表示します。

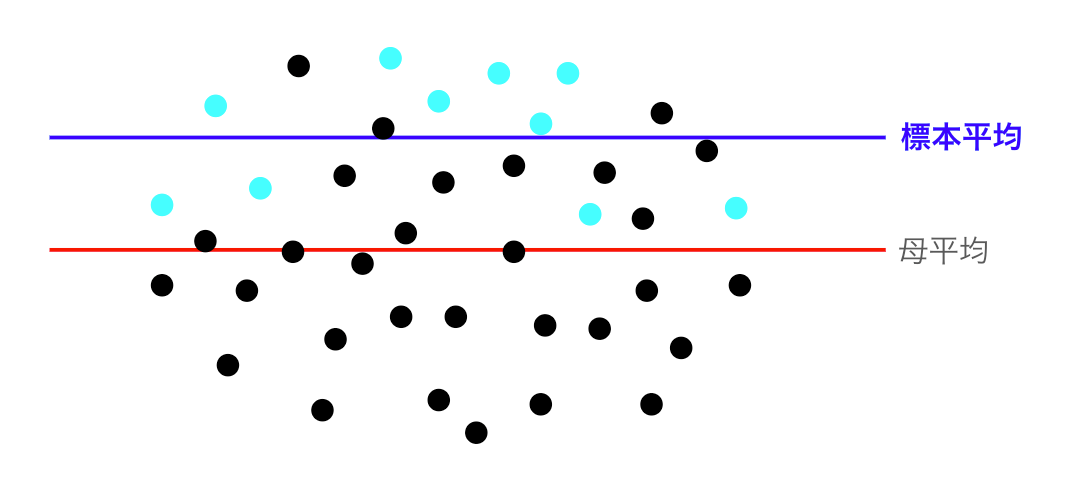
この青点が実際に我々が観測できるデータであり、その平均が標本平均$\bar{X}$になります。

この時、母平均$\mu$と標本平均は$\bar{X}$は、サンプリング時の偏り（図はかなり偏らせていますが）により、ずれていることがわかります。

すると、標本分散$s^2$は標本平均$\bar{X}$を用いて計算され、母分散$\sigma^2$は母平均$\mu$を用いて計算することを期待しているので、明らかに計算結果にズレが生じることがわかります。
もっというと、より標本に対して近い値を持つ標本平均$\bar{X}$を利用した標本分散$s^2$の方が、値が小さくなってしまうように感じると思います。

であるから、不偏分散$u^2$では、その過小評価具合を、$N$ではなく$N-1$で割ることによって補正しているそうです。

しかしながら、なぜ不偏分散$u^2$にて、代わりに割る値が$N-1$で良いのかがわかりません。
上記の説明では、なんとなく小さい値で割ることで、なんとなく分散を補正できるみたいな書き方をされているので、$N-1$という値に妥当性がないよう見えます。

極端な話、$N-1$ではなく、$N-1.000001$ではダメなのか？という質問に回答できません。

したがって、なぜ$N-1$で割ることが、数学的に正しいのかを、導出してみます。

問題設定の導入

不偏分散$u^2$の話に入る前に、文字で問題設定を記述します。

ある母集団と、その標本データ$X$において、下記のような問題設定を考えます。

• 母集団
  • 母平均：$\mu$
    • $\mu = \mathbb{E}[X]$
  • 母分散：$\sigma^2$
    • $\sigma^2 = \mathbb{E}[(X - \mathbb{E}[X])^2]$
  • つまり、各サンプルごとに同分布であることは仮定します。
• 標本
  • 標本データ：$X = {X_1, X_2, \cdots, X_N}$
  • サンプルサイズ：$N$
  • 標本平均：$\bar{X}$
    • $\bar{X} = \dfrac{1}{N} \sum_{i=1}^{N}{X_i}$
  • 標本分散：$s^2$
    • $s^2 = \dfrac{1}{N} \sum_{i=1}^{N}{(X_i - \bar{X})^2}$
  • 不偏分散：$u^2$
    • $u^2 = \dfrac{1}{N-1} \sum_{i=1}^{N}{(X_i - \bar{X})^2}$

導出

考え方

ここで考えるのは、下記が成立するかどうかです。
「標本から得られた標本分散の期待値が母分散と一致するかどうか」

つまり、簡単に説明すると、サンプルサイズ$N$でサンプリングした標本から標本分散を得る作業を無限回実施した場合、その平均がちゃんと母分散と一致するのであれば、標本分散は（各サンプリングごとに偏りはあるにせよ）母分散を過不足なく評価できていることにになります。

例えば、標本平均の期待値は、母平均に一致します。
これは簡単に計算できます。

では、標本分散$s^2$で考えたらどうなるのかを、計算してみます。

補足：標本平均の期待値が母平均に一致すること

$$\mathbb{E}[\bar{X}] = \mathbb{E}[\dfrac{1}{N} \sum_{i=1}^{N}{X_i}]$$

期待値の線形性より

$$= \dfrac{1}{N}\sum_{i=1}^{N}{\mathbb{E}[{X_i}]}$$

問題設定より、各標本$X_i$の期待値は母平均$\mu$なので、

$$= \dfrac{1}{N}\sum_{i=1}^{N}{\mu}$$

$$= \dfrac{1}{N} \cdot N \cdot \mu = \mu$$

したがって、標本平均$\bar{X}$の期待値は、母平均と一致します。

実際の導出

標本分散の式変形

まずは、標本分散$s^2$を計算しやすい形に式変形していきます。
標本分散$s^2$は下記のように書けます

$$s^2 = \dfrac{1}{N} \sum_{i=1}^{N}{(X_i - \bar{X})^2}$$

ここで、$(X_i - \bar{X}) = (X_i - \mu) - (\bar{X} - \mu)$と考えます。

急に出てきた式のように見えるかもしれないですが、先ほど説明した通り、標本平均$\bar{X}$と母平均$\mu$はサンプリングの偏りによって、一般的に一致しません。
標本分散$s^2$では、その偏りを考えずに、標本平均$\bar{X}$を利用していることが、問題でした。

今回の式変形は、標本平均$\bar{X}$と母平均$\mu$との各サンプリングごとの偏りを評価して、標本分散$s^2$を計算するための変形です。

補足　上記の式変形

情緒的な説明を上記でしたので、もう少し、数式から上記の式変形の正当性を見ていきます。
（この式変形がやはり恣意的に感じる部分ではあるので）


将来的に標本分散$s^2$の期待値$\mathbb{E}[s^2]$を考えるので、期待値にしたときに使いやすい形を考えたいです。


ここでの式変形は

$$(X_i - \bar{X}) = (X_i - \mu) - (\bar{X} - \mu)$$

でした。


このときに、$\mathbb{E}[(X_i - \mu)^2]$と$\mathbb{E}[(\bar{X} - \mu)^2]$を考えています。


前者$\mathbb{E}[(X_i - \mu)^2]$は、各標本$X_i$と母平均$\mu$との差の二乗の期待値です。これは各標本$X_i$が、母集団から母集団の確率分布に従ってサンプリングされているという事実から、母分散$\sigma^2$の定義式と一致します。


したがって、

$$\mathbb{E}[(X_i - \mu)^2] = \sigma^2$$

続いて、後者$\mathbb{E}[(\bar{X} - \mu)^2]$は、標本平均$\bar{X}$と母平均$\mu$との差の二乗の期待値です。
これは、標本平均$\bar{X}$の分散に一致し、統計学の基本的な性質から$\dfrac{\sigma^2}{N}$になることが知られています。


したがって、

$$\mathbb{E}[(\bar{X} - \mu)^2] = \dfrac{\sigma^2}{N}$$

このように、両方の期待値から母分散$\sigma^2$の簡単な変形が出てくるため、将来的な期待値の計算に使いやすくなります。
だから、この式変形を行うわけです。

$$s^2 = \dfrac{1}{N} \sum_{i=1}^{N}{(X_i - \bar{X})^2}$$

$$= \dfrac{1}{N} \sum_{i=1}^{N}{\left((X_i - \mu) - (\bar{X} - \mu)^2 \right)}$$

2乗を展開して

$$= \dfrac{1}{N} \sum_{i=1}^{N}{\left((X_i - \mu)^2 -2(X_i - \mu)(\bar{X} - \mu) + (\bar{X} - \mu)^2\right)}$$

$$= \dfrac{1}{N} \left(\sum_{i=1}^{N}{(X_i - \mu)^2} -2(\bar{X} - \mu)\sum_{i=1}^{N}{(X_i - \mu)} + \sum_{i=1}^{N}{(\bar{X} - \mu)^2}\right)$$

$$= \dfrac{1}{N} \left(\sum_{i=1}^{N}{(X_i - \mu)^2} -2(\bar{X} - \mu)\left(\sum_{i=1}^{N}{X_i} - \sum_{i=1}^{N}{\mu}\right) + \sum_{i=1}^{N}{(\bar{X} - \mu)^2}\right)$$

$$= \dfrac{1}{N} \left(\sum_{i=1}^{N}{(X_i - \mu)^2} -2N(\bar{X} - \mu)(\bar{X} - \mu) + N(\bar{X} - \mu)^2\right)$$

$$= \dfrac{1}{N} \left(\sum_{i=1}^{N}{(X_i - \mu)^2} - N(\bar{X} - \mu)^2\right)$$

ここまでで、標本分散$s^2$は下記のように式変形できました。

$$s^2 = \dfrac{1}{N} \left(\sum_{i=1}^{N}{(X_i - \mu)^2} - N(\bar{X} - \mu)^2\right)$$

標本分散の期待値の計算

ここで、標本分散$s^2$の期待値を計算します。

$$\mathbb{E}[s^2] = \mathbb{E}[\dfrac{1}{N} \left(\sum_{i=1}^{N}{(X_i - \mu)^2} - N(\bar{X} - \mu)^2\right)]$$

期待値の線形性より

$$\mathbb{E}[s^2] = \dfrac{1}{N}\sum_{i=1}^{N}{\mathbb{E}[(X_i - \mu)^2]} - \mathbb{E}[(\bar{X} - \mu)^2]$$

補足で上述した通り、下記が成立します。

$$\mathbb{E}[(X_i - \mu)^2] = \sigma^2$$

$$\mathbb{E}[(\bar{X} - \mu)^2] = \dfrac{\sigma^2}{N}$$

以上を代入すると、

$$\mathbb{E}[s^2] = \dfrac{1}{N}\sum_{i=1}^{N}{\mathbb{E}[(X_i - \mu)^2]} - \mathbb{E}[(\bar{X} - \mu)^2]$$

$$= \dfrac{1}{N}\sum_{i=1}^{N}{\sigma^2} - \dfrac{\sigma^2}{N}$$

$$= \dfrac{1}{N} \cdot N \cdot \sigma^2 - \dfrac{\sigma^2}{N}$$

$$= \dfrac{N-1}{N}\sigma^2$$

したがって、

$$\mathbb{E}[s^2] = \dfrac{N-1}{N}\sigma^2$$

以上から、
標本分散$s^2$の期待値は母分散$\sigma^2$と一致しない
ことがわかると思います。

また、標本分散$s^2$は母分散$\sigma^2$の$\dfrac{N-1}{N}$倍で過小評価していたこともわかりました。

不偏分散の導出

ここまでで、標本分散$s^2$の期待値は母分散$\sigma^2$と一致しておらず、過小評価していることを数学的に計算しました。

では、ここで、母分散$\sigma^2$を過不足なく評価できる分散として、
不偏分散$u^2$
を導入し、その値を算出してみます。

$$\mathbb{E}[s^2] = \dfrac{N-1}{N}\sigma^2$$

より、

$$\sigma^2 = \dfrac{N}{N-1}\mathbb{E}[s^2]$$

$$= \dfrac{N}{N-1}\mathbb{E}[\dfrac{1}{N} \sum_{i=1}^{N}{(X_i - \bar{X})^2}]$$

$$=\mathbb{E}[\dfrac{N}{N-1} \cdot \dfrac{1}{N} \sum_{i=1}^{N}{(X_i - \bar{X})^2}]$$

$$=\mathbb{E}[\dfrac{1}{N-1} \sum_{i=1}^{N}{(X_i - \bar{X})^2}]$$

と書けます。
不偏分散$u^2$の期待値が、母分散と一致すると考えると、

$$\sigma^2=\mathbb{E}[u^2]$$

であるはずなので、

$$u^2 = \dfrac{1}{N-1} \sum_{i=1}^{N}{(X_i - \bar{X})^2}$$

となります。

以上から、母分散$\sigma^2$を過不足なく評価できる値である不偏分散$u^2$では、サンプルサイズ$N$ではなく、$N-1$で割り算することになります。

まとめ

ここまで読んでくださりありがとうございました。
（ちょうど統計学を勉強中だったため、このような記事を書かせていただきました）

統計学の検定や評価などはRなどのソフトで非常に簡単に計算が可能ですが、その分誤って理解・利用している人が多く、世の中には間違った検定方法で嘘の結果が示されていることが非常に多いそうです。

統計学を誤解なく正しく利用できるようになるため（それを証明できるように）にも、もう少し勉強したら統計学の資格取得も目指そうと思います。

参考文献

データ分析に必須の知識・考え方 統計学入門 仮説検定から統計モデリングまで重要トピックを完全網羅