勾配降下法 ・ 誤差逆伝播法 を自力で導出する

はじめに

ノーベル物理学賞2024が発表され、我らが神である、ホップフィールド教授とヒントン教授が受賞されましたね。
受賞理由は「人工ニューラルネットワークによる機械学習を可能にする基礎的な発明」です（参考）
この技術を開発したところから、第3次AIブームが始まり、AIが人間を超える分野が次々と現れ、そして、現在の生成AIによる第4次AIブームに繋がっています。

それを記念して、今回の受賞に非常に関係の深い、ニューラルネットワークにおけるコア技術の一つ、「勾配降下法」と「誤差逆伝播法」を取り扱います。

勾配降下法・誤差逆伝播法は深層学習において最重要の知識です。
実際、これらを理解していない状態ではAIの研究はできません。
（使うだけなら簡単に使えてしまうところが、AIのすごいところですが）

微分可能性などを考えないAIの研究者とかいたら嫌ですよね。
私も学生時代に何度も叩き込まれました。

とは言いつつ、いざパッと聞かれたときにド忘れしている可能性はあると思います。
なので、このタイミングで棚卸しておいて、忘れていても大丈夫なようにしようというのが、本記事の目的です。

完全に、自分中心な考えですが、その分、忘れても思い出せるように、厳密性とわかりやすさを両立させた記事を目指して記載していますので、参考になれば幸いです。

本記事は、とにかく誤差逆伝播法を腹落ちしてもらうための記事です。枝葉の精度向上のための工夫など余計なものは記事に書きません。

想定読者

• AIの勉強の初学者
• 誤差逆伝播法の初学者
• 深層学習を使ったことがある人
• 深層学習で出てくる単語（損失関数や活性化関数など）の単語の意味がなんとなくわかる人
• 誤差逆伝播法をド忘れした人
• ある程度数式を追える能力がある人（ある程度で良いです）
• 厳密な理論展開に興味がある人

参考文献

誤差逆伝播法は、下記の文献で学習すれば一発です。
数式だけで理解しても、生き生きした知識になりにくいので、実装してみるのがとてもおすすめです。

ゼロから作るDeep Learning ❸ ―フレームワーク編

そして、ことフレームワークの実装という観点では、上記の書籍を超えるものはないと思います。誤差逆伝播法の知識に加え、実装するために重要な自動微分の概念も、序盤にしっかりと記述されています。
特に、実装がすべてpythonなのも良いです。pytorchなどのメジャーなフレームワークの実装コードでは、誤差逆伝播法の部分は高速化する必要がある都合上、C言語などの別言語で書かれていたり、cuda対応のため、専用の記述がなされており、初学者が読み取るのは無理です。断言してもいいです。

しかしながら、本書籍で作るフレームワークはすべてpythonで書かれているため、深層学習のコアの部分が初学者でも理解できるように書かれているため、下手にpytorchのリポジトリを覗きに行くよりも、実装方法が理解できることが多いです。

とは言っても、500ページ以上ある書籍を勉強し直すのは結構大変なので、誤差逆伝播法に関しては、パッと理解できるように記事を書ければと思います。

議論の流れ

本記事では、一般的な全結合層のニューラルネットワークと取り上げて、それぞれのパーツを数式で表現します。
その後、ネットワークのパラメータを最適化するための学習に必要な技術である、勾配降下法について取り上げて、勾配の重要性をわかってもらった後、勾配の求め方を誤差逆伝播法で説明します。

問題設定

全体像として、非常に簡単な3層の全結合ニューラルネットワーク（NN）を考えます。
図中の丸い部分が特徴量を表し、矢印の線が重みを表します。
また、一番左の5つの列は、最初の特徴量なので入力を表し、一番右の一つは、最後の特徴量なので、ネットワークの出力を表しています。
中間の4つは隠れ層の特徴量です。

これがCNNになろうがTransfomerになろうが、入力と重みの位置関係が若干変わるだけで、理論的には同じ理論で説明できます。

なお、初めはわかりやすさのために具体的な数値を次元とした、ニューラルネットワークで考えますが、記事の後半の「補足」にて、次元数を一般化した際の、論理展開も記載しています。

名前をつける

図を元に名前をつける

各特徴量や重みに名前をつけます。

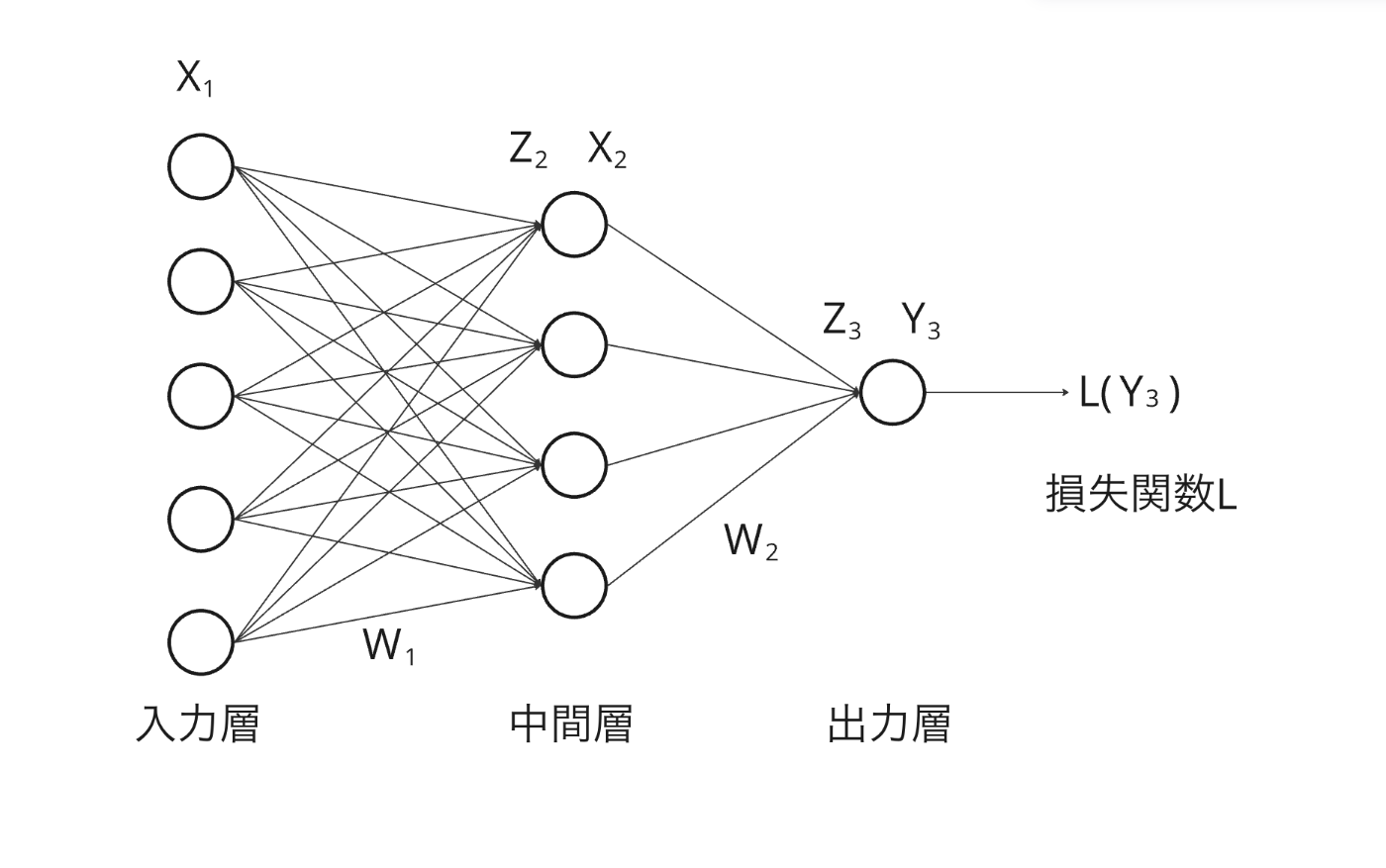
基本的には、上記のように名前をつけます。
ここで、中間層と出力層の特徴量に二つ名前がついていると思いますが、これはこの部分に活性化関数$h$が含まれているからです。
中間層や出力層のある1つの特徴量を拡大すると下記のようになっております。

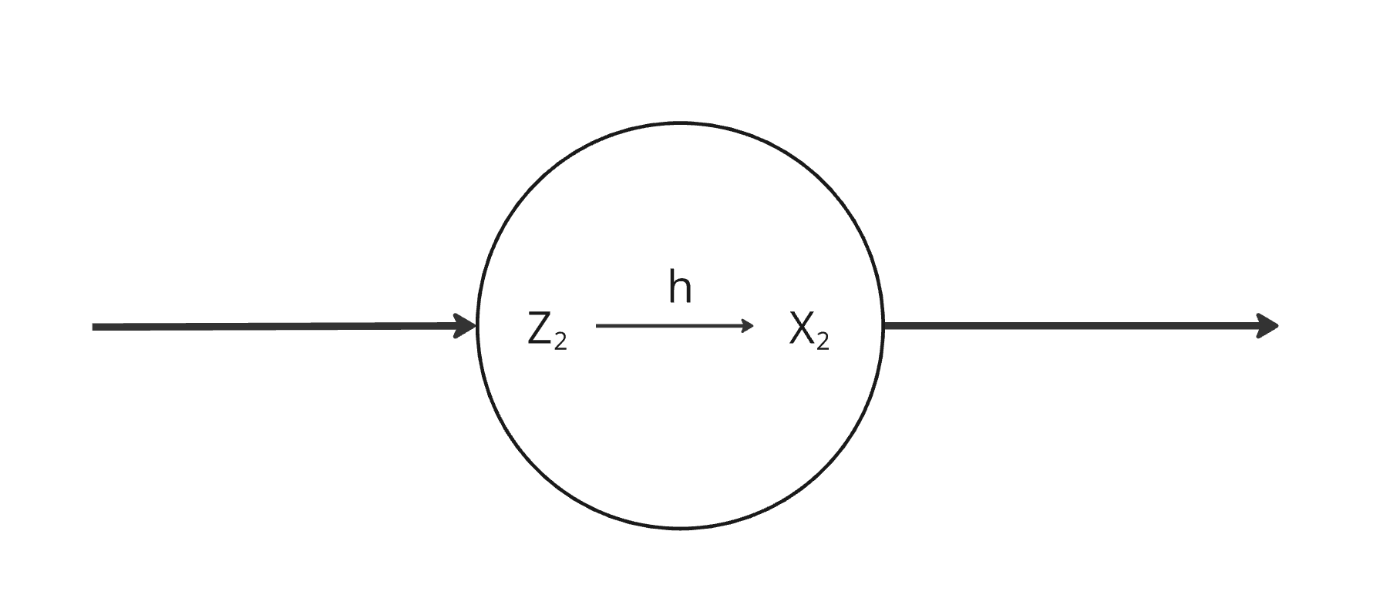
これは、式で書くと下記を表します。

$$X_2 = h(Z_2)$$

この$h$には、中間層であればreluやsigmoid、出力層であれば、sigmoidや恒等関数、softmax関数などが使われますが、今回は、中間層でも出力層でもsigmoid関数を利用することを考えます。

シグモイド関数は下記で定義される関数です。

$$h(x) = \frac{1}{1 + e^{-x}}$$

上記の関数の値域は$0 \leq h(x) \leq 1$となっており、これが出力層でも使われるということは、出力の値の範囲も0以上1以下に制限されているということになります。

さらにsigmoid関数を$x$で微分すると下記のような式になります。

$$\frac{dh}{dx} = h(x)(1 - h(x))$$

このように微分した値に、微分前の式が出てきます。
このような式は、数値計算には非常に相性が良いため、よく利用されます。
（活性化関数のアウトプットをメモリに保存しておけば、微分計算は代入するだけで簡単）

ちなみに、
中間層にてSigmoid関数を活性化関数として利用すると、勾配消失の問題が発生します。
したがって最近では活性化関数にはreluの方がよく使われます(reluの方が微分計算も簡単)。
しかし本題とズレるのでスルーします

特徴量

ここで、図に書けなかった関係を式で記述します。

まず、入力層$X_1$は下記のような要素を持ちます

$$X_1 = \begin{pmatrix} x_{11} \\ x_{12} \\ x_{13} \\ x_{14} \\ x_{15} \end{pmatrix}$$

要素の一つ一つが特徴量の値になります。

同じように下記のような関係性があります。

$$Z_2 = \begin{pmatrix} z_{21} \\ z_{22} \\ z_{23} \\ z_{24} \end{pmatrix}$$

$$X_2 = \begin{pmatrix} x_{21} \\ x_{22} \\ x_{23} \\ x_{24} \end{pmatrix}$$

$$Z_3 = \begin{pmatrix} z_{31} \end{pmatrix}$$

$$Y_3 = \begin{pmatrix} y_{31} \end{pmatrix}$$

重み

また、各層をつなぐ重みは下記のような要素を持ちます。

$$W_1 = \begin{pmatrix} w_{11}^{(1)} & w_{21}^{(1)} & w_{31}^{(1)} & w_{41}^{(1)} & w_{51}^{(1)} \\ w_{12}^{(1)} & w_{22}^{(1)} & w_{32}^{(1)} & w_{42}^{(1)} & w_{52}^{(1)} \\ w_{13}^{(1)} & w_{23}^{(1)} & w_{33}^{(1)} & w_{43}^{(1)} & w_{53}^{(1)} \\ w_{14}^{(1)} & w_{24}^{(1)} & w_{34}^{(1)} & w_{44}^{(1)} & w_{54}^{(1)} \end{pmatrix}$$

$$W_2 = \begin{pmatrix} w_{11}^{(2)} & w_{21}^{(2)} & w_{31}^{(2)} & w_{41}^{(2)} \end{pmatrix}$$

各層での線形結合

ここまでで、入力層$X_1$と中間層$Z_2$の関係は下記のように書くことができます。

$$Z_2 = W_1X_1 = \begin{pmatrix} w_{11}^{(1)} x_{11} + w_{21}^{(1)} x_{12} + w_{31}^{(1)} x_{13} + w_{41}^{(1)} x_{14} + w_{51}^{(1)} x_{15} \\ w_{12}^{(1)} x_{11} + w_{22}^{(1)} x_{12} + w_{32}^{(1)} x_{13} + w_{42}^{(1)} x_{14} + w_{52}^{(1)} x_{15} \\ w_{13}^{(1)} x_{11} + w_{23}^{(1)} x_{12} + w_{33}^{(1)} x_{13} + w_{43}^{(1)} x_{14} + w_{53}^{(1)} x_{15} \\ w_{14}^{(1)} x_{11} + w_{24}^{(1)} x_{12} + w_{34}^{(1)} x_{13} + w_{44}^{(1)} x_{14} + w_{54}^{(1)} x_{15} \end{pmatrix}$$

同様に、中間層$X_2$と出力層$Z_3$の関係は下記のように書くことができます。

$$Z_3 = W_2X_2 = \begin{pmatrix} w_{11}^{(2)} x_{21} + w_{21}^{(2)} x_{22} + w_{31}^{(2)} x_{23} + w_{41}^{(2)} x_{24} \end{pmatrix}$$

なお、ネットワークには通常「バイアス」と呼ばれるものが存在します。これは一次結合の結果に対して、ある定数を足し算することで、オフセットを修正するようなものです。

ただし、今回の例で考えると、入力層と中間層の最後の特徴量を「1」(固定)と考えると、重みの最後の列ベクトルをバイアスとみなすことができるため、バイアスの有無で論理は変わりません。

具体的に、今回の例なら、下記のように考えると、バイアスを考慮できます。

$$Z_2 = W_1X_1 = \begin{pmatrix} w_{11}^{(1)} x_{11} + w_{21}^{(1)} x_{12} + w_{31}^{(1)} x_{13} + w_{41}^{(1)} x_{14} + b_1 \times 1 \\ w_{12}^{(1)} x_{11} + w_{22}^{(1)} x_{12} + w_{32}^{(1)} x_{13} + w_{42}^{(1)} x_{14} + b_2 \times 1 \\ w_{13}^{(1)} x_{11} + w_{23}^{(1)} x_{12} + w_{33}^{(1)} x_{13} + w_{43}^{(1)} x_{14} + b_3 \times 1 \\ w_{14}^{(1)} x_{11} + w_{24}^{(1)} x_{12} + w_{34}^{(1)} x_{13} + w_{44}^{(1)} x_{14} + b_4 \times 1 \end{pmatrix}$$

活性化関数

さらに、活性化関数を用いて、下記の関係性も成立します。
ただし、中間層での損失関数を$h_2$、出力層での損失関数を$h_3$とします。

$$X_2 = h_2(Z_2)$$

$$Y_3 = h_3(Z_3)$$

損失関数

最後に、このネットワークの損失関数$L$を定義します。

損失関数とは、ネットワークの出力の値と、正解の値がどのくらい離れているかを表す指標です。

例えば、ネットワークが翌日の降水確率を予測するようなネットワークの場合、正解の降水確率とネットワークが予測した降水確率の誤差が損失関数になります。
この誤差を小さくすることで、ネットワークは賢くなります。

ここでは、損失関数$L$は平均2乗誤差を利用すると想定します。
平均2乗誤差は、各サンプルの2乗誤差の期待値を計算する必要がありますが、簡単のためサンプル数1で近似した場合、ただの2乗誤差になるため、正解の値を$y'$とすると、損失関数は下記のようになります。

$$L(Y_3) = (Y_3 - y')^2$$

上記の2乗誤差も簡単に微分することができます。
$Y_3$で微分すると

$$\frac{dL}{dY_3} = 2(Y_3 - y')$$

となります。

実は、ここまでで、ネットワークのすべての関係性を数式で書き下すことができました。

学習の目的

損失関数の最小化

ネットワークの学習の目的は、先ほども簡単に触れましたが、損失関数$L$の最小化です。
損失関数$L$を最も小さくするようなネットワークのパラメータを得ることが目的です。

今回でいうパラメータというのは、ネットワークの中における学習可能な部分である、重み$W_1$と$W_2$の値になります。

制約条件がない状態で、ある関数の最小値を得る方法は、その関数をパラメータで微分して0になる点を探すことで求めることができます。
しかしながら、ニューラルネットワークの場合、設定される関数を解析的に解くことはできません。したがって勾配降下法という手法を用います。

勾配降下法

勾配降下法というのは、パラメータを更新するための手法であり、下記のような形で更新することで、損失関数$L$を小さくする方向にパラメータを更新できるという手法です。
更新式は下記のようになります。

$$W_1 ← W_1 - \alpha \dfrac{dL}{dW_1}$$

$$W_2 ← W_2 - \alpha \dfrac{dL}{dW_2}$$

本来は、確率的勾配降下法とかミニバッチ勾配降下法とか、RMSpropやAdamなどの紹介をしたいですが、枝葉の工夫とみなして、今回の記事ではスルーします。

Adamの設計とかは、とても理にかなっていて面白いけど、ぱっと見わかりずらいので初学者には理解しにくいと思うので、機会があったら紹介したいです。

この式で重要なポイントは、パラメータを損失関数$L$の勾配の逆の方向に更新すると、結果として損失関数$L$が小さくなるパラメータを得られるということです。

まずは感覚的な説明

これは、よくみる二次関数の例で説明すると直感的に理解できます。

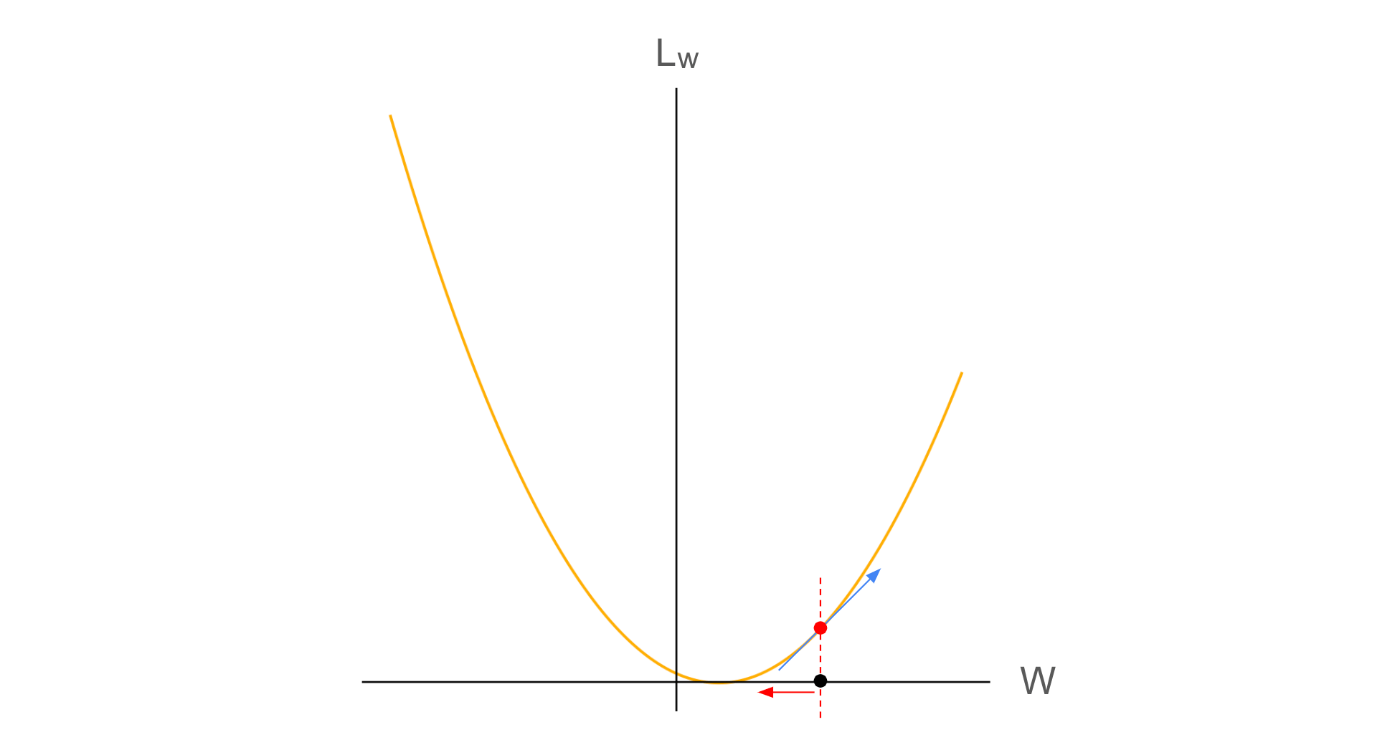
損失関数$L$の値は、ネットワークの出力$Y_3$に依存しますが、ネットワーク出力$Y_3$は、ネットワークパラメータ$W_1$に依存するため、損失関数$L$は、ネットワークパラメータ$W_1$の関数として、表現しても良いです。
したがって、損失関数$L$を$L(W_1)$と書いてみることにします。

グラフ上の黒点をパラメータの初期値$W_1$とすると、そのパラメータでの損失関数の値$L(W_1)$はグラフ上の赤点の値になります。

この場合、青線は、損失関数$L$を$W_1$で微分した際の傾き（勾配）を表しており、その傾きは正です。
微分の定義として、

$$\dfrac{L\text{の増加量}}{W_1\text{の増加量}}$$

で表されます。

ここから、

• 勾配が正の場合
  • 「$W_1$の増加量」を負にすると「$L$の増加量」が負になる
• 勾配が負の場合
  • 「$W_1$の増加量」を正にすると、「$L$の増加量」が負になる

ことがわかります

したがって、勾配と逆の符号で「$W_1$を増加」させることが「$L$の増加量」を負にすることにつながります。

したがって下記のような更新式が作られるわけです。

$$W_1 ← W_1 - \alpha \dfrac{dL}{dW_1}$$

$$W_2 ← W_2 - \alpha \dfrac{dL}{dW_2}$$

ここでの$\alpha$は学習率です。これがないと、更新が単位$W_1$あたりの変化量で更新されてしまうため、微分に近似できません。
なぜなら、微分の定義はあくまで、「$W_1$の変化量が限りなく0に近づく」場合を前提としているからです。

そういう意味で、この変化量の部分を調整しているのが、学習率$\alpha$です。
したがってこの値は、1より小さい値を、利用者が設定することになります。

そして、この値を小さくすることで、より厳密に微分方程式を解くことができます。
しかしながら、解いた結果が最小値になることは保証されていないため、学習率を小さくすることで必ず精度が上がるとは言えません。
（最小値は保証されませんが、厳密に解いた場合は、極小値か鞍点になることは保証されます）

理論的な解説

前節の説明では、直感的なわかりやすさを優先して、2次関数で説明しています。
しかし、実際のニューラルネットワークは2次関数ではないため、一般的な関数で考えます。

今回、損失関数$L(W_1)$を考えた際に、ネットワークパラメータ$W_1$を更新後の損失関数$L(W_1+\Delta W_1)$との関係性に、下記が成立すれば、損失関数が小さくなる方向に学習されていると言えそうです。

$$L(W_1) > L(W_1+\Delta W_1)$$

このとき、式の右辺を、$W_1$周りでテイラー展開で近似することを考えます。

$$L(W_1 + \Delta W_1) \approx L(W_1) + \frac{dL}{dW_1} \Delta W_1 + O(\Delta W_1^2)$$

ここで、$O(\Delta W_1^2)$は微小単位$\Delta W_1$の2乗に支配される値になるため、1次近似の範囲内では無視できる値になります。

テイラー展開とは、ある関数$f(x)$がある時に、ある点$a$付近にて、下記が成立します。

$$f(x) = f(a) + (x-a)\dfrac{df}{dx} + \dfrac{1}{2!}(x-a)^2\dfrac{d^2f}{dx^2} + \cdots + \dfrac{1}{k!}(x-a)^k\dfrac{d^kf}{dx^k} + \epsilon_k$$

ここで$\epsilon_k$は余剰項と呼ばれますが、$k→\infty$に飛ばすと0になることが知られています。

本文中の例では、$a=W_1$、$x = W_1 + \Delta W_1$として考えています。

ここから、2乗の項を無視することで、下記のように考えることができます。

$$L(W_1 + \Delta W_1) \approx L(W_1) + \frac{dL}{dW_1} \Delta W_1$$

その上で、前提条件である$L(W_1) > L(W_1+\Delta W_1)$が成立することを考えると、

$$\frac{dL}{dW_1} \Delta W_1 < 0$$

であることが求められます。
したがって、損失関数$L(W_1)$を小さくする方向$\Delta W_1$というのは、$\dfrac{dL}{dW_1}$と逆の符号であることがわかると思います。

では、どれだけ変化させるかを考えると、テイラー展開の1次近似を考えたため、微小距離だけ変化させることを期待したいです。
（1次近似は、近似先の点が近似元の点から離れるほど、大きく誤差が増える近似のため、変化量は極小にしたいです。逆に言えば、極小の変化量であれば、かなり正確に近似することができます）

したがって、学習率$\alpha<<1$を導入すると、

$$\Delta W_1 = -\alpha \dfrac{dL}{dW_1}$$

なので、下記の更新式が成立します。

$$W_1 ← W_1 + \Delta W_1 = W_1 - \alpha \dfrac{dL}{dW_1}$$

勾配の求め方

ここまでで、どのようにネットワークパラメータ$W_1$、$W_2$を更新することで、損失関数$L$を小さくできそうか、というのがわかったと思います。

問題はどうやって勾配$\dfrac{dL}{dW_1}$、$\dfrac{dL}{dW_2}$を求めるかです。

この勾配さえあれば、下記の更新式にしたがって更新することで、損失関数を小さくすることができます。

$$W_1 ← W_1 - \alpha \dfrac{dL}{dW_1}$$

$$W_2 ← W_2 - \alpha \dfrac{dL}{dW_2}$$

誤差逆伝播法

改めて、今回の図を載せます。この後の議論は図を見ながら考えるとわかりやすいかもです。
（以降の議論は、別のページで常に下記の図を表示しながら見ると理解しやすいです）

ネットワークの全体像

各特徴量ごとの中身

パーツごとの勾配を求める

求めたいのは$\dfrac{dL}{dW_1}$や$\dfrac{dL}{dW_2}$ですが、ネットワークになっているため、直接求めるのは不可能です。

では、何の勾配なら求められそうでしょうか。
ここで、最後の方から各パーツごとの勾配を考えてみようともいます。

出力と損失関数の勾配

ネットワークの出力$Y_3$と損失関数$L$の勾配は求めることができます。
なぜなら損失関数は下記のように定義されており、微分可能だからです。

$$L(Y_3) = (Y_3 - y')^2$$

$$\frac{dL}{dY_3} = 2(Y_3 - y')$$

これは、正解$y'$と出力$Y_3$の値があれば、ただ一つの値に決まります。

出力層と出力結果の微分

続いて、前節で利用した$Y_3$は、すでに説明済みですが、下記の式によって算出されています。

$$Y_3 = h_3(Z_3)$$

ここで$h_3$は活性化関数Sigmoidであり、下記のように定義されています。

$$h_3(Z_3) = \frac{1}{1 + e^{-Z_3}}$$

この関数は、単純な関数であるので、それぞれの入出力で微分することができます。具体的には下記です。

$$\frac{dY_3}{dZ_3} = h(Z_3)(1 - h(Z_3))$$

これも、出力層の活性化関数に入力する前の値$Z_3$があれば、ある一定の値に決まります。

2つ目の重みと出力層の微分

続いて、前節で利用した、出力層の値$Z_3$は下記のように算出されます。

$$Z_3 = W_2X_2 = \begin{pmatrix} w_{11}^{(2)} x_{21} + w_{21}^{(2)} x_{22} + w_{31}^{(2)} x_{23} + w_{41}^{(2)} x_{24} \end{pmatrix}$$

これも当然、2つ目の重み$W_2$と出力層$Z_3$は簡単に微分することができます。

$$\frac{dZ_3}{dW_2} = X_2^T$$

となります。

詳細な話

本来は本文で書くことですが、
以下の内容は少し数式を追う難易度が上がるので、
数式を追いたくない方は、そっと閉じてください。

ここでは、$\dfrac{dZ_3}{dW_2}$の詳細な求め方について解説します。


ここで、今回の例ではなく、一般的な例を考えます。


$N$次元の$X$と$M$次元の$Y$を考えた時、重み行列をW（$M \times N$次元）とすると、下記が成立します。

$$Y=WX$$

ここで、出力$Y$の$i$次元目の値を考えると、下記のようになります。

$$Y_i = \sum_{j=1}^{N}{W_{ij}X_j}$$

ここで、ある重み成分$W_{kl}$で微分することを考えます。

$$\dfrac{dY_i}{dW_{kl}} = \dfrac{d}{dW_{kl}} \left( \sum_{j=1}^{N}{W_{ij}X_j} \right)$$

ここでクロネッカーのデルタ$\delta_{ik}$を導入すると、下記のように書けます。

$$\dfrac{dY_i}{dW_{kl}} = X_l \delta_{ik}$$

すなわち

$$\dfrac{dY_i}{dW_{il}} = X_l$$

上記をもとに行列として書き下すと、下記のようになります。

$$\dfrac{dY}{dW} = \begin{pmatrix} X_1 & X_2 & \cdots & X_N \\ X_1 & X_2 & \cdots & X_N \\ \vdots & \vdots & \ddots & \vdots \\ X_1 & X_2 & \cdots & X_N \\ \end{pmatrix}$$

ここで、$\dfrac{dY}{dW}$は$M \times N$次元（Wと同じ）です。


さて、結果だけ見ると非常に簡単な行列ですね。考えてみれば当然で、$\dfrac{dY}{dW}$は、$X$を固定したときに、$W$を変化させたときの$Y$の変化量になります。
行列積は線形結合になるため、1次関数の微分と同様に微分したら$X$が出てくるのは当然です。

クロネッカーのデルタ$\delta_{il}$の定義は下記の通りです。

$$\delta_{ij} = \begin{cases} 1 & \text{if } i = j \\ 0 & \text{if } i \neq j \end{cases}$$

誤差逆伝播法を適用する

ここまで、下記の勾配を取得してきました。

$$\dfrac{dL}{dY_3} = 2(Y_3 - y')$$

$$\dfrac{dY_3}{dZ_3} = h(Z_3)(1 - h(Z_3))$$

$$\dfrac{dZ_3}{dW_2} = X_2^T$$

ただし、$\dfrac{dL}{dY_3}$と$\dfrac{dY_3}{dZ_3}$はスカラー、$\dfrac{dZ_3}{dW_2}$は$1$行$4$列の行ベクトルです。

そして、勾配降下法によりパラメータ更新に利用したい勾配は、$\dfrac{dL}{dW_2}$です。

ここで連鎖律（チェーンルール）を考えます。
連鎖律というのは下記で定義されるものです。

連鎖律

$y=f(g(x))$という形の合成関数に関して、その微分は下記のように計算されます

$$\frac{dy}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx}$$

そして、今回の全結合層において、中間層の出力$X_2$を「固定」した場合、損失関数$L$は下記のように分解することができます。

$$L(Y_3) = L(h_3(Z_3)) = L(h_3(W_2X_2))$$

つまり、連鎖律により、下記のように書くことができます。

$$\dfrac{dL}{dW_2} = \dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_3}{dW_2}$$

そして、各パーツはすでに微分を求めているので、下記のように書くことができます。

$$\dfrac{dL}{dW_2} = 2(Y_3 - y') \cdot h(Z_3)(1 - h(Z_3)) \cdot X_2^T$$

この式も$1$行$4$列の行ベクトルになっていますので、$dW_2$を同じ大きさの行列です。

したがって、重み$W_2$は、下記のように更新すれば、損失関数を小さくする方向に更新できます。

$$W_2 ← W_2 - \alpha \dfrac{dL}{dW_2} = W_2 - \alpha(2(Y_3 - y') \cdot h(Z_3)(1 - h(Z_3)) \cdot X_2^T)$$

1つ目の重みに対して考える

前節にて、$W_2$の更新ができたので、続いて$W_1$の更新を考えます。

全く同じ議論を行うことで、下記の勾配を求めることができます。これまでの議論を理解していれば、以下の数式は容易に理解できるはずです。

$$\dfrac{dZ_3}{dX_2} = W_2$$

$$\dfrac{dX_2}{dZ_2} = h(Z_2)(1 - h(Z_2))$$

$$\dfrac{dZ_2}{dW_1} = \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{15} \\ x_{11} & x_{12} & \cdots & x_{15} \\ \vdots & \vdots & \ddots & \vdots \\ x_{11} & x_{12} & \cdots & x_{15} \\ \end{pmatrix}$$

ただし、$\dfrac{dZ_3}{dX_2}$は$1$行$4$列の行ベクトル、$\dfrac{dX_2}{dZ_2}$は$4$行$1$列の列ベクトル、$\dfrac{dZ_2}{dW_1}$は$4$行$5$列の行列です。

ここから連鎖律により、

$$\dfrac{dL}{dW_1} = \dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_3}{dX_2} \cdot \dfrac{dX_2}{dZ_2} \cdot \dfrac{dZ_2}{dW_1}$$

とかけますが、単純にそのまま計算することはできません。
なぜなら、後半の層とは異なり、入力層と中間層がともに複数あるため、各ニューロンが独立に計算されているのか、他のニューロンに依存しているのかを考慮する必要があるからです。

ただし、それらを一旦考えなければ、下記のように書くことができます。

厳密な議論は、難易度が高いので、「補足:一般化して解く」の中で実施します。
ただ、厳密な議論がわからなくても、ここまでで、おおよそ誤差逆伝播法の理解はできていると思います。

$$\dfrac{dL}{dW_1} = 2(Y_3 - y') \cdot h(Z_3)(1 - h(Z_3)) \cdot W_2 \cdot h(Z_2)(1 - h(Z_2)) \cdot \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{15} \\ x_{11} & x_{12} & \cdots & x_{15} \\ \vdots & \vdots & \ddots & \vdots \\ x_{11} & x_{12} & \cdots & x_{15} \\ \end{pmatrix}$$

とかけるので、重み$W_1$は、下記のように更新すれば、損失関数を小さくする方向に更新できます。

$$W_1 ← W_1 - \alpha \dfrac{dL}{dW_1}$$

これにて、ネットワーク内のすべてのパラメータの更新が完了しました。

計算の補足

$\dfrac{dZ_3}{dX_2} = W_2$の計算だけは解説していないので、難しくはないのですが、一応計算方法を紹介します。


一般化して$Y$を$M$次元の列ベクトル、$X$を$N$次元の列ベクトルとして、$W$をM行N列の行列として、$Y=WX$を考えた時に、その勾配$\dfrac{dY}{dX}$を求めたい。


出力$Y$の$i$次元目の要素は下記のように表せます。

$$Y_i = \sum_{j=1}^{N}{W_{ij}X_j}$$

ここで、ある入力$X_l$で微分することを考えます。

$$\dfrac{dY_i}{dX_l} = \dfrac{d}{dX_l} \left( \sum_{j=1}^{N}{W_{ij}X_j} \right)$$

ここで、明らかに$j=l$の時だけ微分結果の値を持つため、

$$\dfrac{dY_i}{dX_l} = W_{il}$$

したがって、すべての要素に関して同様に考えると、

$$\dfrac{dY}{dX} = W$$

となります。

補足:一般化して解く

余力がある人は、下記をご覧ください。（読まなくても問題ないです）


ここでは、

$$\dfrac{dL}{dW_1}$$

が本当に計算可能かどうかを、完全に一般化して考えてみます。

「計算可能」というのは、行列式などの次元が本当に正しく揃っているのかどうか、という意味です。

また、$\dfrac{dL}{dW_2}$より、$\dfrac{dL}{dW_1}$の方が、論証が難しく、$\dfrac{dL}{dW_2}$に関しても同様の議論で計算可能なことを示せるので、$\dfrac{dL}{dW_2}$の論証は、ここでは省略します。
（難しい方だけ実施します）

さて、ここでは、一般化のため、下記のように定義します。

• 入力層の次元数は$N$
• 中間層の次元数は$H$
• 出力層の次元数は$M$

すると、

• $W_1$は$H \times N$行列
• $W_2$は$M \times H$行列

となります。


この状態で、各パーツごとの勾配の次元を確認し、計算可能かどうかをみていきます。


一般化したので、一旦連鎖律の状態までさか戻り、これが途中で止まれずに最後まで計算可能かどうかを考えます。

$$\dfrac{dL}{dW_1} = \dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_3}{dX_2} \cdot \dfrac{dX_2}{dZ_2} \cdot \dfrac{dZ_2}{dW_1}$$

連鎖律を一般化したニューラルネットで考える

まず、$\dfrac{dL}{dY_3}$は、出力層の次元が$M$のため、一般化した考えると下記のようになります。

$$\dfrac{dL}{dY_3} = \begin{pmatrix} 2(y_{31} - y_{1}') \\ 2(y_{32} - y_{2}') \\ \vdots \\ 2(y_{3M} - y_{M}') \\ \end{pmatrix}$$

これは、$M$行$1$列の列ベクトルであり、出力$Y_3$と同じ形にになります。
（なお、各要素ごとの2乗誤差の和を損失関数としています。）

続いて、$\dfrac{dY_3}{dZ_3}$を考えると、単純に$Z_3$を活性化関数Sigmoidに入れて、微分した結果のため、

$$\dfrac{dY_3}{dZ_3} = h(Z_3)(1 - h(Z_3))$$

となります。
これは当然$Z_3$と同じ形であるため、$M$行$1$列の列ベクトルです。


このとき、$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3}$の計算が可能かどうかを考えます。

$$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} = \begin{pmatrix} 2(y_{31} - y_{1}') \\ 2(y_{32} - y_{2}') \\ \vdots \\ 2(y_{3M} - y_{M}') \\ \end{pmatrix} \cdot h(Z_3)(1 - h(Z_3)) = \begin{pmatrix} 2(y_{31} - y_{1}') \\ 2(y_{32} - y_{2}') \\ \vdots \\ 2(y_{3M} - y_{M}') \\ \end{pmatrix} \cdot \begin{pmatrix} h(z_{31})(1 - h(z_{31})) \\ h(z_{32})(1 - h(z_{32})) \\ \vdots \\ h(z_{3M})(1 - h(z_{3M})) \\ \end{pmatrix}$$

ここまでの計算の流れの中で、各要素は独立に計算されているため、この部分の計算は要素積で問題ありません。
したがって、下記のようになります。

$$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} = \begin{pmatrix} 2(y_{31} - y_{1}')h(z_{31})(1 - h(z_{31})) \\ 2(y_{32} - y_{2}')h(z_{32})(1 - h(z_{32})) \\ \vdots \\ 2(y_{3M} - y_{M}')h(z_{3M})(1 - h(z_{3M})) \\ \end{pmatrix}$$

今後、この計算結果は利用しますが、要素の中身が長すぎるため、下記の通り簡略化します。

$$\left( \dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \right)_i = k_{i}$$

続いて、$\dfrac{dZ_3}{dX_2}$を考えると、これは上の補足で一般化して説明した通り$W_2$となります。
$W_2$は$M \times H$行列でした。


したがって、$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_3}{dX_2}$の計算が可能かどうか考えます。


ここで、直接$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_3}{dX_2}$を考えるのは難しいです。
なぜなら、複数のニューロンがお互いに依存関係を持ちながら接続されているからです。


そこで、まずは$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_{3}}{dx_{2m}}$を考えます。


ここで

$$\dfrac{dz_{3l}}{dx_{2m}} = \dfrac{d}{dx_{2m}}\left( \sum_{j=1}^{N}{w_{lj}^{(2)}x_{2j}} \right) = w_{lm}^{(2)}$$

になります。

ここで重要なのは、中間層$X_2$の$m$番目のニューロンは、次の層$Z_3$での、すべてのニューロンと接続されているため、誤差逆伝播法は下記のように考える必要があります。

$$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_{3}}{dx_{2m}} = k_{1}\dfrac{dz_{31}}{dx_{2m}} + k_{2}\dfrac{dz_{32}}{dx_{2m}} + \cdots + k_{M}\dfrac{dz_{3M}}{dx_{2m}}$$

以上より、

$$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_{3}}{dX_{2}} = \begin{pmatrix} k_{1}\dfrac{dz_{31}}{dx_{21}} + k_{2}\dfrac{dz_{32}}{dx_{21}} + \cdots + k_{M}\dfrac{dz_{3M}}{dx_{21}} \\ k_{1}\dfrac{dz_{31}}{dx_{22}} + k_{2}\dfrac{dz_{32}}{dx_{22}} + \cdots + k_{M}\dfrac{dz_{3M}}{dx_{22}} \\ \vdots \\ k_{1}\dfrac{dz_{31}}{dx_{2H}} + k_{2}\dfrac{dz_{32}}{dx_{2H}} + \cdots + k_{M}\dfrac{dz_{3M}}{dx_{2H}} \\ \end{pmatrix}= \begin{pmatrix} k_{1}w_{11}^{(2)} + k_{2}w_{21}^{(2)} + \cdots + k_{M}w_{M1}^{(2)} \\ k_{1}w_{12}^{(2)} + k_{2}w_{22}^{(2)} + \cdots + k_{M}w_{M2}^{(2)} \\ \vdots \\ k_{1}w_{1H}^{(2)} + k_{2}w_{2H}^{(2)} + \cdots + k_{M}w_{MH}^{(2)} \\ \end{pmatrix}$$

となります。
これは、$H$行$1$列の列ベクトルになります。


続いて、$\dfrac{dX_2}{dZ_2}$を考えると単純に$Z_2$を活性化関数Sigmoidに入れて、微分した結果のため、

$$\dfrac{dX_2}{dZ_2} = h(Z_2)(1 - h(Z_2))$$

となります。
これは当然$Z_2$と同じ形であるため、$H$行$1$列の列ベクトルです。


したがって、$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_{3}}{dX_{2}}$も$\dfrac{dX_2}{dZ_2}$の$H$行$1$列の列ベクトルであり、活性化関数での操作は各ニューロンで独立であるため、

$$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_{3}}{dX_{2}} \cdot \dfrac{dX_2}{dZ_2} = \begin{pmatrix} k_{1}w_{11}^{(2)} + k_{2}w_{21}^{(2)} + \cdots + k_{M}w_{M1}^{(2)} \\ k_{1}w_{12}^{(2)} + k_{2}w_{22}^{(2)} + \cdots + k_{M}w_{M2}^{(2)} \\ \vdots \\ k_{1}w_{1H}^{(2)} + k_{2}w_{2H}^{(2)} + \cdots + k_{M}w_{MH}^{(2)} \\ \end{pmatrix} \cdot \begin{pmatrix} h(z_{21})(1 - h(z_{21})) \\ h(z_{22})(1 - h(z_{22})) \\ \vdots \\ h(z_{2H})(1 - h(z_{2H})) \\ \end{pmatrix}$$

$$=\begin{pmatrix} h(z_{21})(1 - h(z_{21}))(k_{1}w_{11}^{(2)} + k_{2}w_{21}^{(2)} + \cdots + k_{M}w_{M1}^{(2)}) \\ h(z_{22})(1 - h(z_{22})) (k_{1}w_{12}^{(2)} + k_{2}w_{22}^{(2)} + \cdots + k_{M}w_{M2}^{(2)}) \\ \vdots \\ h(z_{2H})(1 - h(z_{2H}))(k_{1}w_{1H}^{(2)} + k_{2}w_{2H}^{(2)} + \cdots + k_{M}w_{MH}^{(2)} ) \\ \end{pmatrix}$$

となります。当然$H$行$1$列の列ベクトルです。
ここで、また、要素が長くなってきたので、下記のように簡略化します。

$$\left(\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_{3}}{dX_{2}} \cdot \dfrac{dX_2}{dZ_2}\right)_s = t_{s}$$

さて、最後です。
$\dfrac{dZ_2}{dW_1}$を考えます。ここでも複数ニューロンの影響を考慮するため、単一重みに絞って、$\dfrac{dz_{2g}}{dw_{gf}^{(1)}}$を考えます。

$$\dfrac{dz_{2g}}{dw_{gf}^{(1)}} = x_{1f}$$

となります。加えて、$e$と$g$が異なる場合、

$$\dfrac{dz_{2e}}{dw_{gf}^{(1)}} = 0$$

です。以上から、

$$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_{3}}{dX_{2}} \cdot \dfrac{dX_2}{dZ_2}\dfrac{dz_{2g}}{dw_{gf}^{(1)}} = t_{g}x_{1f}$$

となるため、

$$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3} \cdot \dfrac{dZ_{3}}{dX_{2}} \cdot \dfrac{dX_2}{dZ_2} \cdot \dfrac{dZ_2}{dW_1} = \begin{pmatrix} t_{1}x_{11} & t_{1}x_{12} & \cdots & t_{1}x_{1N} \\ t_{2}x_{11} & t_{2}x_{12} & \cdots & t_{2}x_{1N} \\ \vdots & \vdots & \ddots & \vdots \\ t_{H}x_{11} & t_{H}x_{12} & \cdots & t_{H}x_{1N} \\ \end{pmatrix}$$

となり、計算できました。
そして、上記こそが連鎖律による$\dfrac{dL}{dW_1}$であり、その行列は$W_1$と同等の$H \times N$行列になっていることがわかりました。


したがって、上記の行列にしたがって、勾配降下法により、各要素を更新することで、重みパラメータを更新できます。


また、せっかくなので実装コードと比較してみましょう。

参考書籍で実装するDeZeroというPytorchライクの深層学習ライブラリでは、下記のように全結合層が定義されています。

class Linear(Function):
    def forward(self, x, W, b):
        y = x.dot(W)
        if b is not None:
            y += b
        return y

    def backward(self, gy):
        x, W, b = self.inputs
        gb = None if b.data is None else sum_to(gy, b.shape)
        gx = matmul(gy, W.T)
        gW = matmul(x.T, gy)
        return gx, gW, gb

誤差逆伝播法で利用する、全結合層の微分結果はbackwardメソッドにて実装されており、gyというのは、後の層の微分結果の累積です。(つまり、$y=Wx$と考えたときの$\dfrac{dL}{dy}$ということです。)


見て欲しいのはgWの部分で、ここでは、全結合層のみの微分結果x.Tに対して、これまでの層からの微分結果の累積gyとの行列積を計算しています。
x.Tは$N$行$1$列の列ベクトルでgyは$1$行$M$列の行ベクトルになります。
その上で行列積を計算することにより、gWは$N \times M$行列となり、下記のようになります。

$$\dfrac{dL}{dW_1} = \begin{pmatrix} x_1 gy_1 & x_1 gy_2& \cdots & x_1 gy_M \\ x_2 gy_1 & x_2 gy_2& \cdots & x_2 gy_M \\ \vdots & \vdots & \ddots & \vdots \\ x_N gy_1 & x_N gy_2 & \cdots & x_N gy_M \\ \end{pmatrix}$$

ただし、

$$gy = (gy_1, gy_2, \cdots, gy_M )$$

$$y＝Wx$$

$$x = (x_1, x_2, \cdots, x_N)$$

となっております。
コードを基準にすると、各特徴量が列ベクトルになることに注意してください。

また、これまでの式変形から得られた最終的な$\dfrac{dL}{dW_1}$は下記でした。

$$\dfrac{dL}{dW_1} = \begin{pmatrix} t_{1}x_{11} & t_{1}x_{12} & \cdots & t_{1}x_{1N} \\ t_{2}x_{11} & t_{2}x_{12} & \cdots & t_{2}x_{1N} \\ \vdots & \vdots & \ddots & \vdots \\ t_{H}x_{11} & t_{H}x_{12} & \cdots & t_{H}x_{1N} \\ \end{pmatrix}$$

なお、$t_{i}$もまた、後の層の勾配の累積になるので、$t_{i} = gy_i$です。


ここで、コードから得られた結果と、数式から得られた結果が転置されている結果になっていることがわかると思います。

これは、数式で表すときは、特徴量は列ベクトルで表現した方が行列積などに都合が良いですが、コードで実装する時は、特徴量を行ベクトルで表現する方が、都合が良いという事情が影響しています。
（例えば、コードを書くとき、a=[0,1,2]のように書くことが多いと思います。これは行ベクトルです）

また、特徴量も重み行列もどちらも転置されているのであれば、線形代数の理論上、問題ないことが知られています。
行列の転置には、すごく便利な下記の変形が成立します。

$$Y^T = (WX)^T = X^TW^T$$

したがって、順番を逆にすれば、最後まで転置した状態で全く同じ議論を行うことができるので、勾配自体も転置したものが得られているわけです。

ちなみに、$\dfrac{dL}{dW_1}$と$\dfrac{dL}{dW_2}$で共通の項があると思います。
下記の式の部分です。

$$\dfrac{dL}{dY_3} \cdot \dfrac{dY_3}{dZ_3}$$

実際にコードで実装する場合には、この計算結果はメモリに保持しておくなどして、複数回同じ計算をしないように工夫しています。

その他補足・学習率の決め方

ここまでで、勾配$\dfrac{dL}{dW_1}$、$\dfrac{dL}{dW_2}$の求め方と、それを用いたパラメータ更新の方法についてご説明してきました。

注意していただきたいのは、勾配$\dfrac{dL}{dW_1}$、$\dfrac{dL}{dW_2}$というのは、あくまで、$dW_1$もしくは、$dW_2$以外のパラメータをすべて固定させたときの、損失関数$L$の変化量になるため、正確には下記の表記が正しいです。

$$\frac{\partial L}{\partial W_1}, \frac{\partial L}{\partial W_2}$$

（記事を書いている途中で気づいたのですが、全部書き換えるのは大変だったのでそのまま突き進みました。）

また、勾配降下法では、各パラメータごとに独立で、損失関数$L$を小さくするようにパラメータを更新しますが、パラメータや層の数が増加すると、パラメータを変化させたことによる積み重ねが、すべて損失関数$L$に対して影響されます。
したがって、一つ一つのパラメータは極小の更新でも、結果として損失関数$L$にかかる影響が大きくなってしまい、極小値を超えて更新してしまうことがあります。
（それが、結果として局所最適化を防ぐことになり、良い影響を与えることもありますが、重みパラメータが壊れ、発散してしまうことも珍しくないです）

したがって、一般に、層やパラメータの数が多い際は、学習率$\alpha$のパラメータを小さく、そうやパラメータの数が少ないシンプルなモデルなら、学習率$\alpha$のパラメータは大きくした方が、スムーズに学習が進むことが、経験的にも多いです。
（学習率を小さくしすぎると、局所最適化の問題や、学習時間の増大の問題が発生します）

また、勾配降下法では、各パラメータは独立（他のパラメータが固定である前提）のときの、パラメータの勾配を知ることができ、パラメータを更新する方向を得ます。
しかし、実際の学習では、全パラメータが同時に更新されるため、$W_1$が固定なら$W_2$はこっちに動かした方がいいけど、$W_1$がその方向に更新されるなら$W_2$は別の方向に更新した方が実はよかった、ということが起こり得ます。

上記に対処する方法は各種提案されております。
例えば、勾配降下法において、適応的な学習率を用いる更新式（Optimizer）を利用することです。

今回、勾配降下法に利用した更新式は、最も単純な更新式ですが、実際にはAdamやRMSpropなどといった、高度な更新式が提案されています。
特にAdamやRMSpropでは、パラメータごとに異なる学習率が適応的に設定され、急な勾配や緩やかな勾配などに対して適応的に振る舞うため、すべてのパラメータを安定して更新することができます。
これにより、パラメータ間での依存関係により、更新方向が最適でなかったとしても、大事故は起こりにくくなります。

さらにAdamでは、Momentumという勾配の更新方向に慣性を持たせる手法も入っています。これにより、過去の勾配も考慮したより滑らかな更新が可能になるため、パラメータの更新が他のパラメータの更新に強く依存しているような場合でも、過去の動きに基づいて滑らかかつ適切な方向に更新が行われやすくなります。（一回の大事故的な更新が行われにくくなります）

他にもBatch Normalizationという手法もあり、各ミニバッチごとに中間層の出力を、平均0分散1に正規化することで、パラメータ間の相互作用の影響を減らす効果が期待でき、安定した学習に寄与します。

まとめ

わかりやすく書くと言ったな。それは嘘だ。

はい、大変申し訳ございませんでした。
最初はわかりやすく書こうと思っていたのですが、厳密性を重視した結果、かなり骨太の内容になってしまったと思います。

ただ、誤差逆伝播法はわかってしまうと、本質自体は簡単な手法なので、どんなに難解に書かれていても、大体理解できます。

この記事に書いてある内容をスラスラ理解できたら、誤差逆伝播法の理解は完璧です！
（責任転嫁）

ここまで読んでくださってありがとうございました！