因果探索で推定した因果グラフをPythonで比較する

はじめに

こんにちは、因果探索アプリケーションCausalas開発の井手です。

因果探索で推定した因果グラフを評価する方法はいくつかありますが、今回はPythonで因果グラフ同士を比較する方法について説明します。

本記事で扱う因果グラフは、因果探索の結果として推定された隣接行列を用いて作成したDAG（有向非巡回グラフ）を想定しています。DAGは、ノード（変数）とそれを繋ぐエッジ（因果関係）で構成されています。

因果グラフ比較の使いどころ

因果グラフを比較する場面として、以下を想定しています。

• 因果探索アルゴリズムの性能評価
  真の因果グラフと推定した因果グラフを比較することで、因果探索の性能を評価したいとき
• 属性が異なるデータセットによる違いを確認
  例えば、男性と女性のデータセットで推定した因果グラフに対して、差分を確認するとき
• 条件設定による違いを確認
  事前知識や独立性検定の有意水準など、条件設定を変更した因果グラフを比較したいとき

比較方法

因果グラフを比較する指標について説明します。指標として、因果グラフ同士の差分を求めるSHD（Structural Hamming Distance） と、真の因果グラフに対して推定した因果グラフの当てはまりを評価する混同行列を用いた指標の2通りを紹介します。

SHD（Structural Hamming Distance）

SHDは、2つの因果グラフの構造的な距離を表す指標で、エッジの増減とエッジの方向の違いをカウントすることで計算します。SHDが小さいほど因果グラフは距離が近いと判断できます。
本記事では以下の論文^[1]を元に、欠けているエッジ、余分なエッジ、逆向きのエッジの3種類をカウントします。

混同行列を用いた指標には真値と推定値の区別がありますが、SHDにはありません。対称的なので、グラフ1からグラフ2への距離とグラフ2からグラフ1への距離は同じです。

混同行列を用いた指標

混同行列

混同行列とは、陽性と陰性に分類する二値分類問題において、推定モデルを評価するために分類結果をまとめた行列のことです。

• TP（True Positive）
  推定値がPositive（陽性）のとき、その分類が正しい場合を指します。
• TN（True Negative）
  推定値がNegative（陰性）のとき、その分類が正しい場合を指します。
• FP（False Positive）
  推定値がPositive（陽性）のとき、その分類が誤りの場合を指します。
• FN（False Negative）
  推定値がNegative（陰性）のとき、その分類が誤りの場合を指します。

Precision, Recall, F1-score

また、混同行列をもとに推定モデルを評価する指標としてPrecision, Recall, F1-scoreがあります。

• Precision（適合率）
  Positive（陽性）と推定したデータの中で真値がPositiveだった確率を指します。

  $$\text{Precision} = \frac{TP}{TP + FP}$$

• Recall（再現率）
  真値のPositive（陽性）のデータの中で正しくPositiveを推定できた確率を指します。

  $$\text{Recall} = \frac{TP}{TP + FN}$$

• F1-score
  PrecisionとRecallの調和平均を指します。

  $$\text{F1-score} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}$$

因果グラフの比較に適用

これらの指標を因果グラフの比較に適用するため、エッジの位置と方向が正しい場合のみPositive（陽性）と分類し、誤りの場合はNegative（陰性）と分類します。

• Precision
  因果のグラフ比較では、推定した因果グラフのエッジの数のうち、2つの因果グラフでエッジの位置と方向が一致している数の割合を計算します。
• Recall
  因果グラフの比較では、真の因果グラフのエッジの数のうち、2つの因果グラフでエッジの位置と方向が一致している数の割合を計算します。

因果グラフの比較を実践する

では、実際にPythonを使って因果グラフを比較してみます。

準備

今回は因果グラフを隣接行列で表し、エッジがあれば1、エッジが無ければ0を代入することとします。

import numpy as np
B_true = np.array([
    [     0,      0,      0,      0,      0,      0],
    [     0,      0,      0,      1,      1,      1],
    [     0,      0,      0,      0,      0,      0],
    [     0,      0,      1,      0,      0,      0],
    [     0,      0,      1,      0,      0,      0],
    [     0,      0,      1,      0,      0,      0]
])
B_est = np.array([
    [     0,      0,      0,      0,      1,      0],
    [     0,      0,      0,      0,      1,      0],
    [     0,      0,      0,      0,      1,      0],
    [     0,      0,      0,      0,      0,      0],
    [     0,      0,      0,      0,      0,      0],
    [     1,      1,      1,      0,      0,      0]
])

真の因果グラフをB_true、推定した因果グラフをB_estとして設定しました。
設定した因果グラフを図で表すと以下のようになります。
同じ位置同士のエッジを見比べると、一致するエッジ、欠けているエッジ、余分なエッジ、逆向きのエッジの4種類の組み合わせがあります。

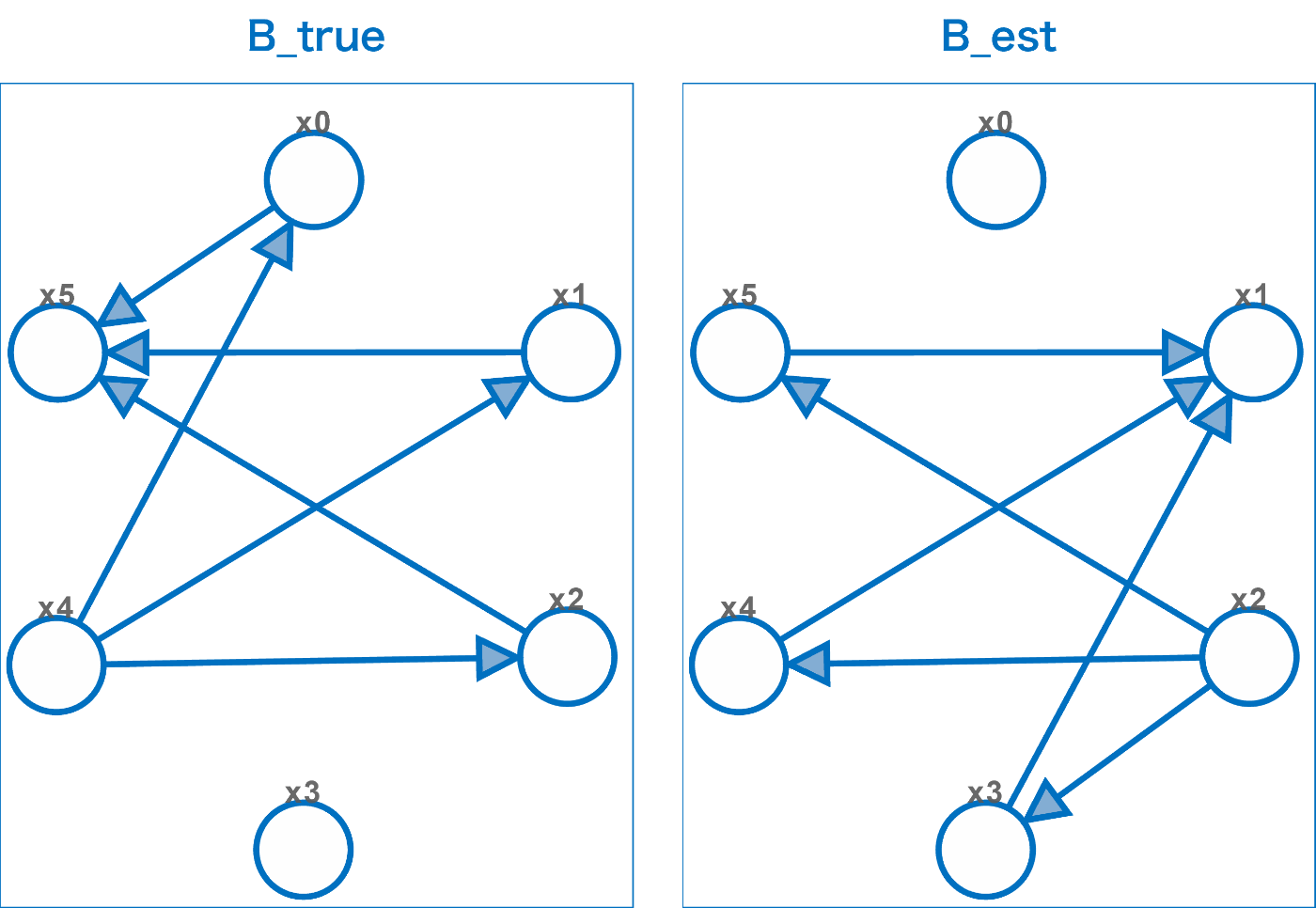
計算

各指標の計算は以下のようになりました。SHDはエッジの差分を計算してカウントし、Precision, Recall, F1-scoreはScikit-learnのmetricsモジュールを使用して計算しています。

from sklearn import metrics

# 異なるエッジの個数をカウント
diff_edges = np.sum(B_true != B_est)
# 逆向きのエッジの個数をカウント
reversed_edges = np.sum(B_true + np.transpose(B_est) == 2)

# SHD
shd = diff_edges - reversed_edges
print(f'SHD = {shd}') # SHD = 6

# 一次元に変換
y_true = B_true.ravel()
y_est = B_est.ravel()

# Precision
precision = metrics.precision_score(y_true, y_est)
print(f'Precision = {precision:.5f}') # Precision = 0.33333
# Recall
recall = metrics.recall_score(y_true, y_est)
print(f'Recall = {recall:.5f}') # Recall = 0.33333
# F1-score
f1 = metrics.f1_score(y_true, y_est)
print(f'F1-score = {f1:.5f}') # F1-score = 0.33333

混同行列から Precision, Recall, F1-score を計算することも可能です。

TN, FP, FN, TP = metrics.confusion_matrix(y_true, y_est).ravel()
print(f'TN = {TN}, FP = {FP}, FN = {FN}, TP = {TP}') # TN = 26, FP = 4, FN = 4, TP = 2
print(f'Precision = {TP/(TP+FP):.5f}') # Precision = 0.33333
print(f'Recall = {TP/(TP+FN):.5f}') # Recall = 0.33333
print(f'F1-score = {2*((precision*recall)/(precision+recall)):.5f}') # F1-score = 0.33333

宣伝：Causalas の因果グラフ比較機能

弊社が開発しているCausalas にも、因果グラフの比較機能があります（v1.1以降）。

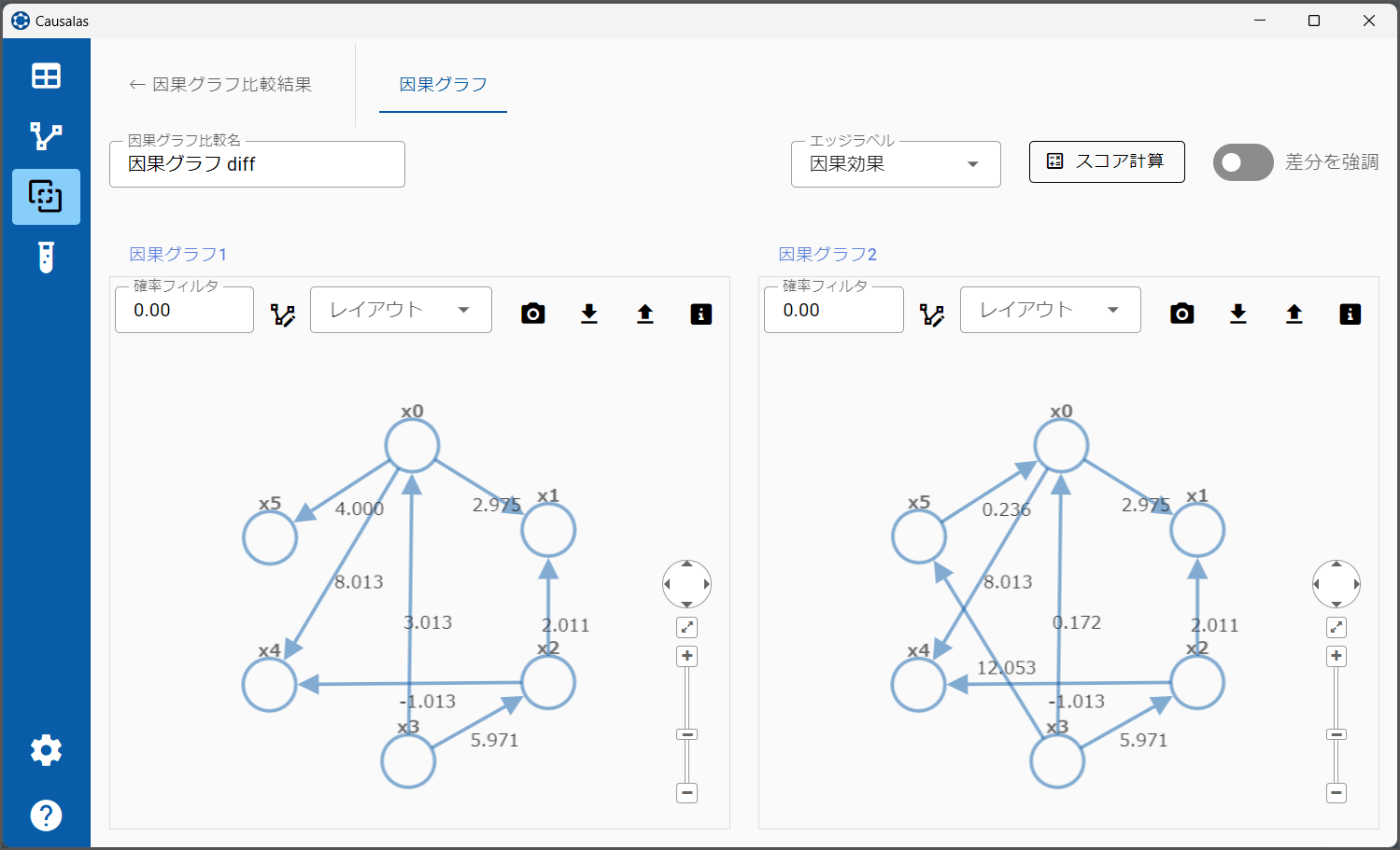
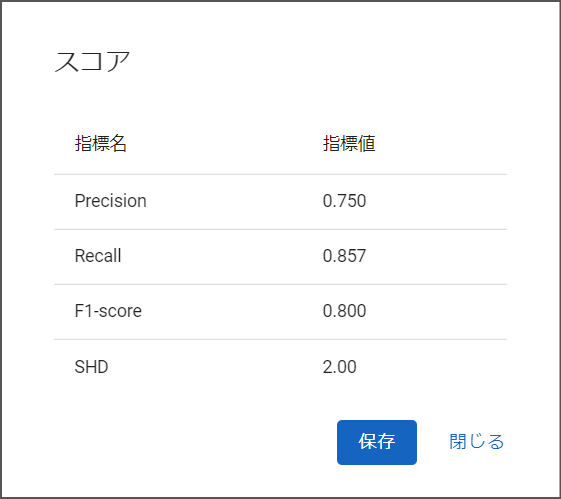
比較したい因果グラフを選択して[スコア計算]ボタンを押すとダイアログが表示され、2つの因果グラフを比較した結果が表示されます。PrecisionやRecallは、左の因果グラフを真の因果グラフ、右の因果グラフを推定した因果グラフと仮定して計算しています。

また、[差分を強調]スイッチをオンにすると、増減したエッジや方向の違うエッジが強調表示されます。

おわりに

Pythonで因果グラフ同士を比較する方法について、以下の手法を説明しました。

• SHD（Structural Hamming Distance）
• Precision, Recall, F1-score

後者は混同行列を使用していますので、Accuracy（正解率） のように混同行列を用いた他の指標を計算することも可能です。データの特性に応じて指標を選択してください。

脚注

1. Tsamardinos, I., Brown, L.E. & Aliferis, C.F. The max-min hill-climbing Bayesian network structure learning algorithm. Mach Learn 65, 31–78 (2006).