LiNGAMで因果探索する際の前処理の実践①：データのクレンジング

はじめに

こんにちは、因果探索アプリケーション Causalas 開発の井手です。

今回は、因果探索アルゴリズムの一つであるLiNGAMを用いた因果探索における、前処理について調査しました。
LiNGAMに関連する論文を中心に調査を行い、因果探索する際に共通して実施される前処理として、異常値や不要な変数の除去といったデータクレンジングの手法に焦点を当て、まとめましたので紹介します。

LiNGAMの実行前に行うべき正規性や線形性の確認といった概観分析については、こちらの記事を参照してください。

異常値のクレンジング

一般的なデータ分析と同様に、因果探索においても異常値の存在は分析結果の信頼性に大きな影響を与えるため、適切な処理が不可欠です。多くの研究では、こうした異常値を事前に削除または補間する手法が採用されています。

外れ値

因果探索の精度を高めるため、多くの論文では、外れ値の除去が標準的な前処理として実施されています。外れ値の判定には、以下のような一般的な手法が用いられています。

• ヒストグラムや箱ひげ図などの可視化手法を用いて、明らかに異常と判断される値を外れ値として識別する
• データの下位5%および上位95%といったパーセンタイルに基づき、極端な値を除去する
• 平均値と標準偏差を用いて、平均±3σ（シグマ）を超える値を外れ値とみなす

欠損値

欠損値の処理は、データの性質や分析目的に応じて削除または補間されますが、実施するかどうかは慎重に判断する必要があります。

例えば以下の論文では、欠損値を前月のデータで補間しています。

Changing Regional Price Relationships in Retail Fresh Broiler/Fryer Whole Chicken Prices^[1]

この研究は、アメリカの各地域における生鮮ブロイラーの小売価格を分析しており、価格がランダムウォークに従うという仮定に基づき、欠損値を前月の価格で補間する手法が採用されています。

一方、以下の論文では欠損値を削除するアプローチが取られています。

Does Financial Literacy Impact Investment Participation and Retirement Planning in Japan?^[2]

この研究では、日本における金融リテラシーが投資行動や退職計画に与える影響を分析しています。
アンケート調査において「その他」や「わからない/答えたくない」といった回答を欠損値として扱い、該当データを削除しています。

ただし、欠損値の削除には慎重な対応が求められます。たとえば、収入や金融資産に関する質問に対して「わからない/答えたくない」と答える傾向がある回答者は、非常に高所得または低所得といった特定の属性に偏っている可能性があり、分析結果にバイアスが生じるリスクが指摘されています。

このように、欠損値を処理する際には、データの分布や特性を十分に理解したうえで適切な方法を選択することが重要です。

変数のクレンジング

多変量データセットを扱う際には、計算時間が増加し、因果探索の結果が複雑になるといった課題が生じることがあります。こうした問題に対応するため、いくつかの研究では、因果探索に用いる変数の数を適切に絞り込む手法が導入されています。

変化の少ない変数

LiNGAMアルゴリズムは、主に連続変数を対象とした手法であるため、値が一定の変数（定数）（下図のヒストグラム(a)）や、変動が極めて少ない変数（下図のヒストグラム(b)）は、因果関係の推定に寄与しない可能性が高く、前処理の段階で除外されることがあります。

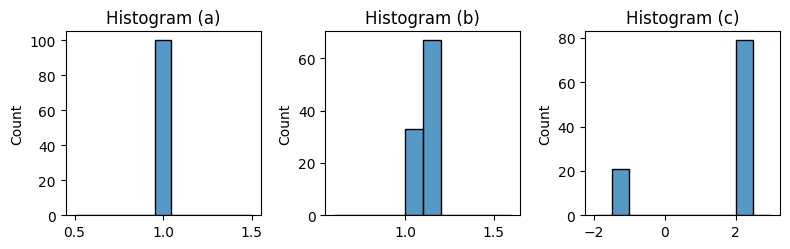
このような変数は、他の変数との関連性が乏しく、因果関係が推定されないケースが多いためです。

例えば以下の論文では、分析対象期間を通じて変化が見られなかった変数を除外する処理が行われています。

Causal analysis of nitrogen oxides emissions process in coal-fired power plant with LiNGAM^[3]

この研究では、石炭火力発電所における窒素酸化物（NOx）排出の要因を特定するために因果関係を分析しています。
前処理時に、石炭銘柄の変更中に取得されたデータなどの非定常運転データ、外れ値とノイズの多いデータに加えて、分析期間を通じて変化が見られなかった定数的な変数を削除しています。

一方で、明確に二値に分かれる変数（上図のヒストグラム(c)）は、定数的な変数とは異なり、因果関係が推定される可能性があります。こうした変数を除外することで未観測共通原因として機能し、因果構造の推定に影響を与えるリスクがあります。
ただし、ドメイン知識などに基づき、その変数が未観測共通原因として作用しないと判断できる場合には、変数を除外した上でLiNGAMを適用することが有効な選択肢となります。
また、未観測共通原因の存在を仮定した因果探索アルゴリズムを実行することも一つの方法です。
未観測共通原因の存在を仮定したアルゴリズムには、BottomUpParceLiNGAM^[3:1]、RCD^[4]、CAM-UV^[5]などがあります。

また、二値変数への因果効果を計算する際は、こちらの記事を参考にしてください。

相関の無い変数

相関係数を用いて変数間の関係性を評価し、対象変数と相関が無いと判断された変数を除外することで、次元削減を図る手法があります。
特に、因果関係を分析したいターゲット変数が存在する場合、因果効果の相殺が生じていなければターゲット変数と相関のない変数を削除しても未観測共通原因として機能する可能性は低いと考えられます。

ただし、相関係数の数値がどれだけ大きい変数を選択すればよいかという基準が無いため選択は難しく、除外した変数が未観測共通原因になる可能性には常に注意が必要です。

次元削減の一手法として、K-meansクラスタリングと相関係数を組み合わせて変数を選択している論文もあります。

Causality-Inspired Models for Financial Time Series Forecasting.^[6]

この研究では、金融資産のリターン予測を目的として、まずデータセットに対してK-meansクラスタリングを実施し、各クラスター内の変数とターゲット変数とのピアソンの相関係数を算出して、その結果に基づき、各クラスターから最も相関の高い変数を選定することで、クラスター毎に代表変数を1つに絞り込む手法を採用しています。

しかしこのような手法は、効率的な次元削減ができる一方で、削除した変数が未観測共通原因になるリスクがあるため、慎重な検討が必要です。

おわりに

本記事では、LiNGAMを実行する前に行うべき不要なデータをクレンジングするための前処理について解説しました。外れ値や欠損値の削除、次元削減など、一般的なデータ分析に使用される前処理はLiNGAMアルゴリズムの実行時においても高い頻度で使用されていますが、因果探索の精度に大きく影響するため実行には注意が必要です。
これらの前処理を適切に行うことで、LiNGAMの結果の信頼性が高まり、より意味のある因果関係を導き出すことができます。

脚注

1. K. Duangnate, J. W. Mjelde. Changing Regional Price Relationships in Retail Fresh Broiler/Fryer Whole Chicken Prices. Journal of Agricultural and Applied Economics, 55(4): 609-625, 2023.

2. Y. Jiang and S. Shimizu. Does Financial Literacy Impact Investment Participation and Retirement Planning in Japan?. arXiv:2405.01078, 2024.

3. T. Tashiro, S. Shimizu, A. Hyvärinen, T. Washio. ParceLiNGAM: a causal ordering method robust against latent confounders. Neural computation, 26(1): 57-83, 2014.

4. T. N. Maeda and S. Shimizu. RCD: Repetitive causal discovery of linear non-Gaussian acyclic models with latent confounders. In Proc. 23rd International Conference on Artificial Intelligence and Statistics (AISTATS2020), Palermo, Sicily, Italy. PMLR 108:735-745, 2020.

5. T. N. Maeda and S. Shimizu. Causal additive models with unobserved variables. In Proc. 37th Conference on Uncertainty in Artificial Intelligence (UAI). PMLR 161:97-106, 2021.

6. D. C. Oliveira, Y. Lu, X. Lin, M. Cucuringu, A. Fujita. Causality-Inspired Models for Financial Time Series Forecasting. arXiv:2408.09960, 2024.