ディレクショナルライト・ポイントライト・スポットライトの実装
本記事ではライトの実装方法について紹介します。
ライトの種別
本記事で実装するライトの種別は以下のとおりです。各ライトの詳細は本文を参照してください。
- ディレクショナルライト
- ポイントライト
- スポットライト
ライトカラーの設定方法
ライト実装の前に、ライトカラーの設定方法について述べておきます。
ライトカラーはRGBで表します。通常のカラーは
ディレクショナルライト
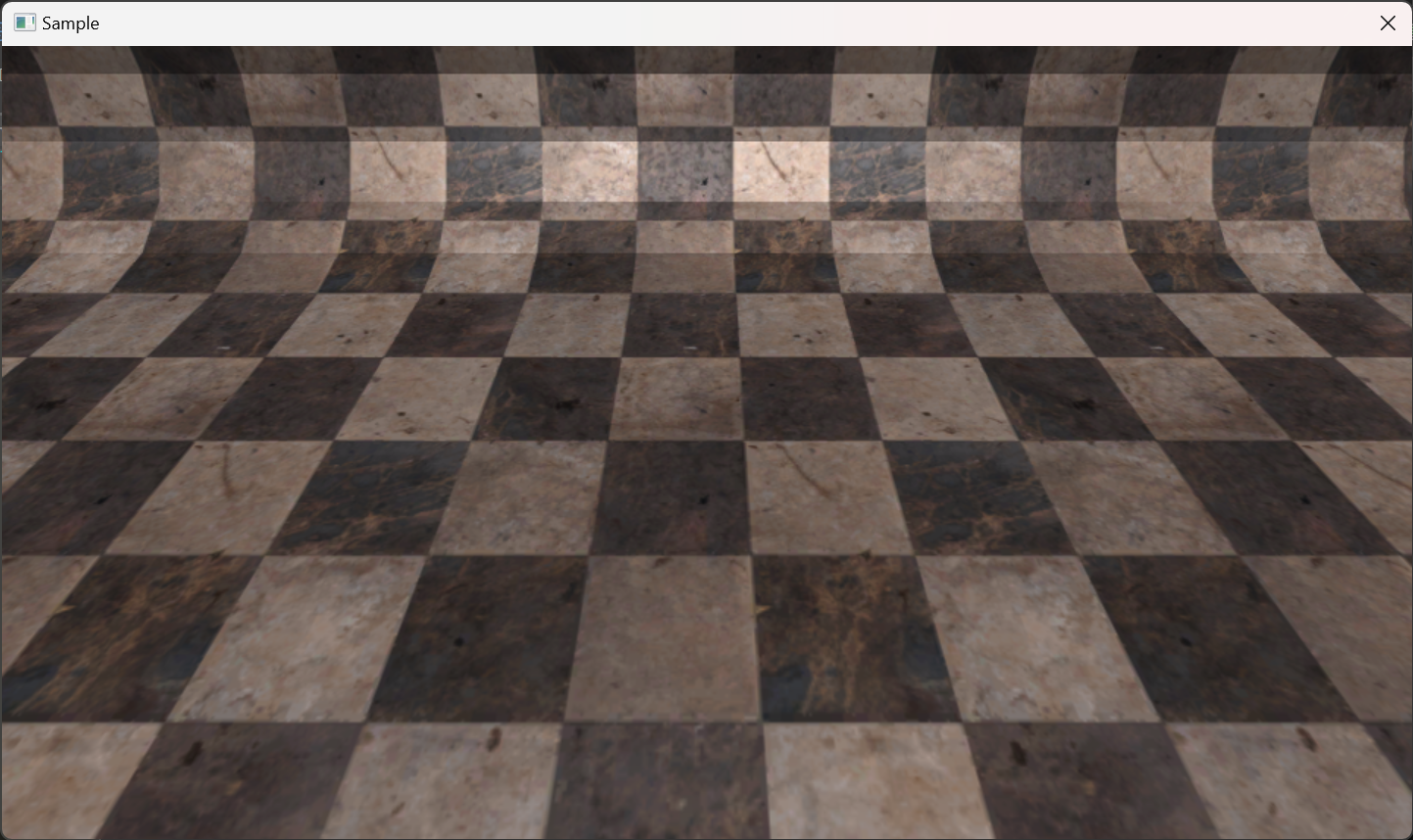 ディレクショナルライトの例
ディレクショナルライトの例
ディレクショナルライトは、方向のみをもつ光源です。平行光源とも呼ばれます。シーン中のどこであっても照らされる方向が同じになるようなライトです。よく太陽光のかわりとして用いられます。
ディレクショナルライト設定値
ディレクショナルライトの実装に必要な設定値は以下のとおりです。
| 設定 | 値の形式 |
|---|---|
| ライトカラー | RGB(ベクトル) |
| ライト強度 | スカラー |
| ライト方向 | ベクトル |
ライト方向については、ディレクショナルライトの計算に使うのではなくBRDFの計算のために使います。
ディレクショナルライトの実装
まず設定値は全て定数なので、コンスタントバッファとして定義しておきます。
レジスタの値は適当です。
cbuffer CbLight : register(b1)
{
float3 LightColor : packoffset(c0); // ライトカラー
float LightIntensity : packoffset(c0.w); // ライト強度
float3 LightForward : packoffset(c1); // ライト方向
}
ディレクショナルライトの実装は以下のとおりです
float3 EvaluateDirectionalLight
(
float3 lightColor,
float lightIntensity
)
{
return lightColor * lightIntensity;
}
ライトの向きと照度の関係
LightForwardが使われてないじゃないか、と思われるかもしれません。ディレクショナルライトのカラーはライト方向に依存しないため、ライトカラーの計算にLightForwardは出てきません。
じゃあどこでLightForwardを使うかというと、照度(照らされている光の強さ)の調整のために使用されます。このことについて、もう少し詳しく解説します。まずは↓の図をみてください。
サーフェイス(黄色のラインで表現)に対し上から垂直にディレクショナルライト(白色で表現)が当たっている様子を示したものです。レーザー光線が上から当たっているようなものだと考えてください。ディレクショナルライトが当たっている範囲を
このライトを少し傾けてみます。
ライトを傾けてみると、光が当たっている範囲がやや広くなったことがわかるかと思います。ライトを傾けたときに光が当たっている範囲を
| 記号 | 説明 |
|---|---|
| 法線ベクトル。大きさは1 | |
| 光源ベクトル。大きさは1 |
このとき、ライトを傾けただけでライトの強さは変わっていません。しかし、照射範囲は広くなったため(EvaluateDirectionalLight関数の内部には組み込んでいません。
(\bold{n}\cdot\bold{l})
今回の実装では、最終的にライトカラーとBRDFを乗算する際に
saturateを使って0,1範囲にクランプするようにします。
// ライトカラー
float3 lit = EvaluateDirectionalLight(
LightColor,
lightIntensity
);
// 出力カラー
float3 outputColor = saturate(dot(N, L)) * BRDF * lit;
ポイントライト
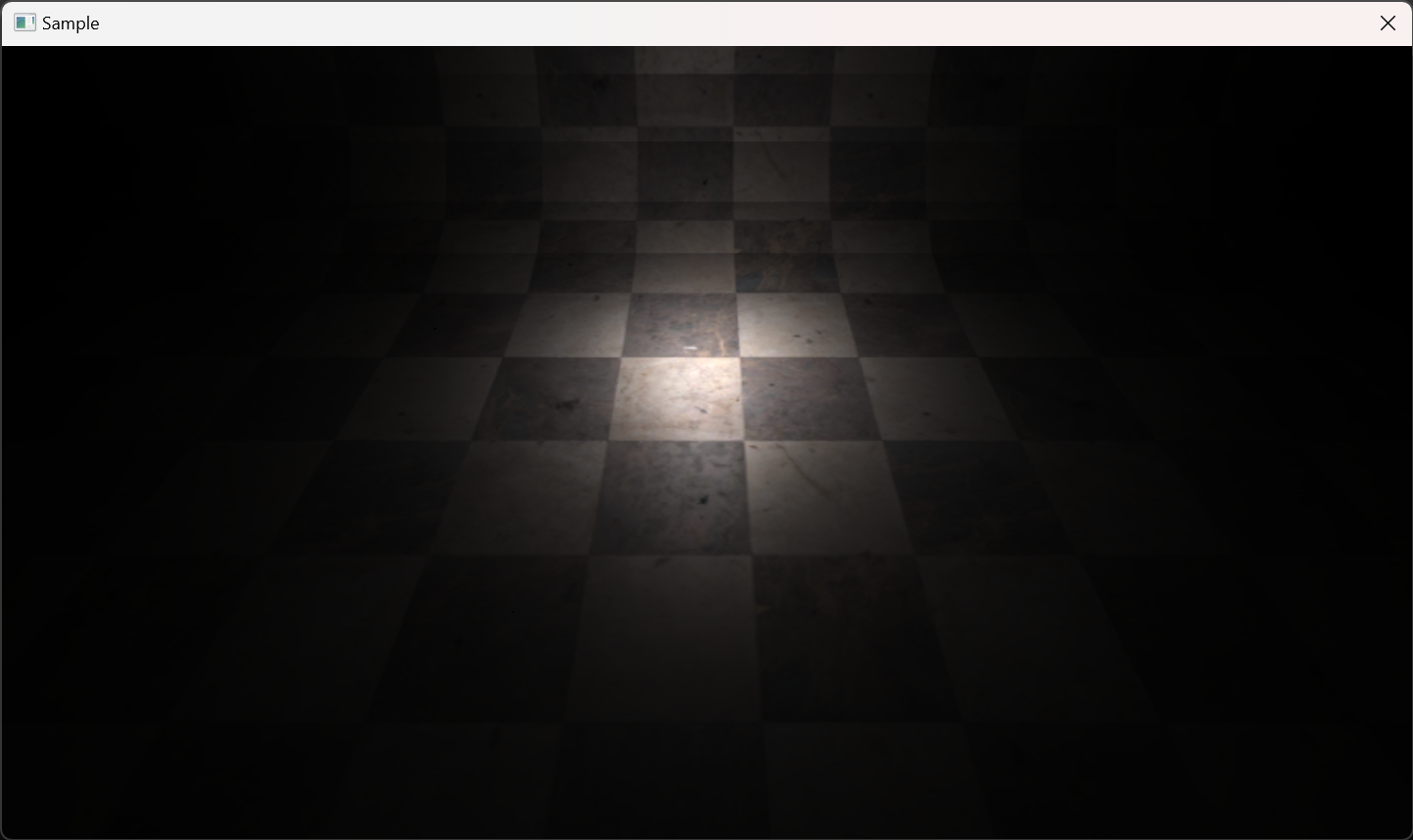 ポイントライトの例
ポイントライトの例
ポイントライトは、大きさがなく全ての方向に同じ強さの光を発するライトです。光は光源の位置から球状に広がっていきます。
距離による減衰(ポイントライト)
ディレクショナルライトと違い、ポイントライトには距離による光の減衰が起こります。
距離による減衰とは、光源から離れれば離れるほど光の強さが弱くなっていく現象のことです。
※図
ポイントライトが距離によってどれくらい減衰していくかは、逆二乗の法則に従います。
| 記号 | 説明 |
|---|---|
| 照度 | |
| 光度 | |
| ライトからの距離 |
いきなり照度や光度といった物理量をだしてしまいましたが、逆二乗の法則は光学(物理学)の分野で定義されているものなので物理量で表しました。とりあえずは、光源と照らされている箇所の距離が離れるほど、距離の2乗に反比例して暗くなっていく(照度
ライトとの距離が0になるとき
先程でてきた逆二乗の法則の式ですが、
この問題の解決法はとても単純で、max関数などで調整すればOKです。
float d = 5;
float d2 = d*d;
float min_d = 0.01;
float attenuation = 1.0f / (max(d2, min_d));
光が届く限界の距離
減衰が逆二乗の法則に従うとすると、距離が遠くなるに連れてどんどん光が弱くなっていくことがわかります。
ただし、どれだけ距離が遠くなっても光の強さが0になることはありません。強さが0になるには距離を無限大にする必要があります。
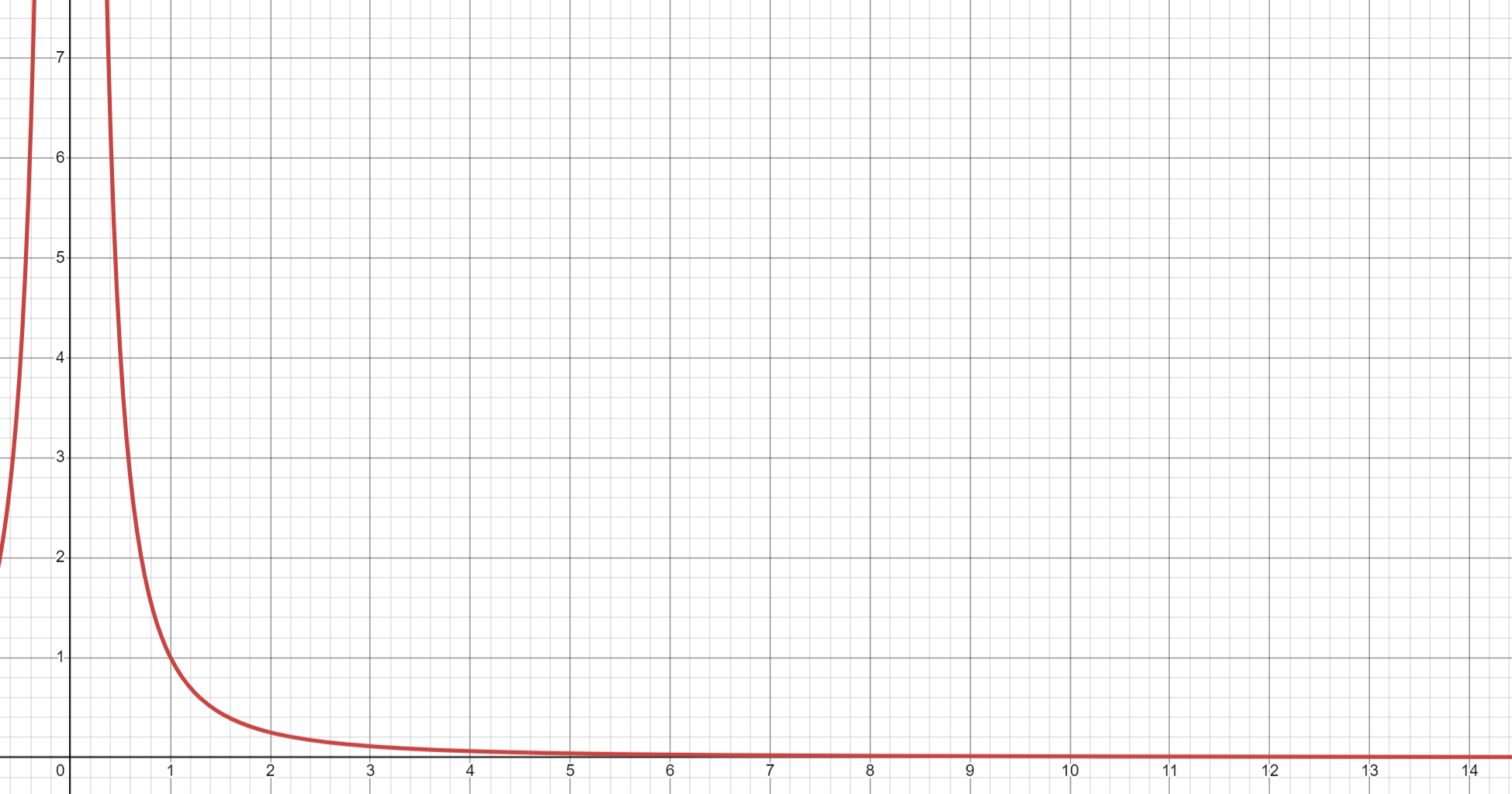 横軸が距離、縦軸が光の強さを表す
横軸が距離、縦軸が光の強さを表す
光の強さが殆ど0になっている場合は思い切って光が届いていないことにし、ライティングに関する処理をスキップして処理負荷を低減させたいところです。例えば、「距離が5m以上離れたらもう光は届いていないことにする」と決めて、ライティング計算するポイントがライトから5m以上離れていたらライティング計算処理自体をスキップする、といったことです。
こういったある範囲を決めて範囲外のものを除外する処理をカリングといいます。ライトのカリングの場合はライトカリングといったりします。
ライトカリングを実装するとき、「ライトからの距離が閾値を超えたら処理をスキップする」と単純に実装してしまうと、閾値のところで急に暗くなってしまいます。
 閾値周辺で突然暗くなり、エッジが目立つ
閾値周辺で突然暗くなり、エッジが目立つ
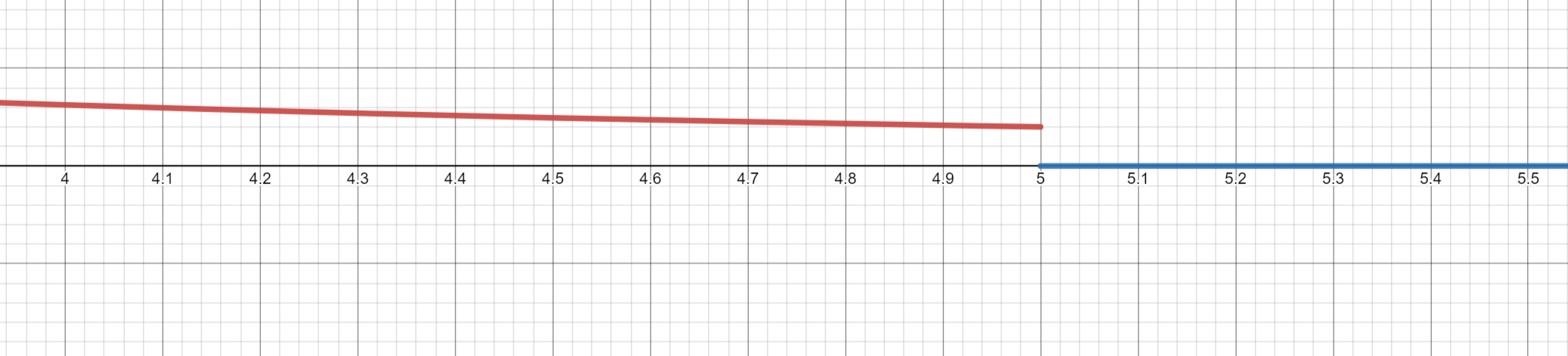 明るさをグラフにしたもの。横軸が距離、縦軸が明るさを表す。距離が閾値(5)を超えたときに急に明るさが0になっている
明るさをグラフにしたもの。横軸が距離、縦軸が明るさを表す。距離が閾値(5)を超えたときに急に明るさが0になっている
閾値周辺はスムーズに暗くなっていくようにしたいです。そのため、閾値周辺でスムーズに0になっていくような関数を乗算します。この説明だとよくわからないと思いますので、次のグラフを見てください。
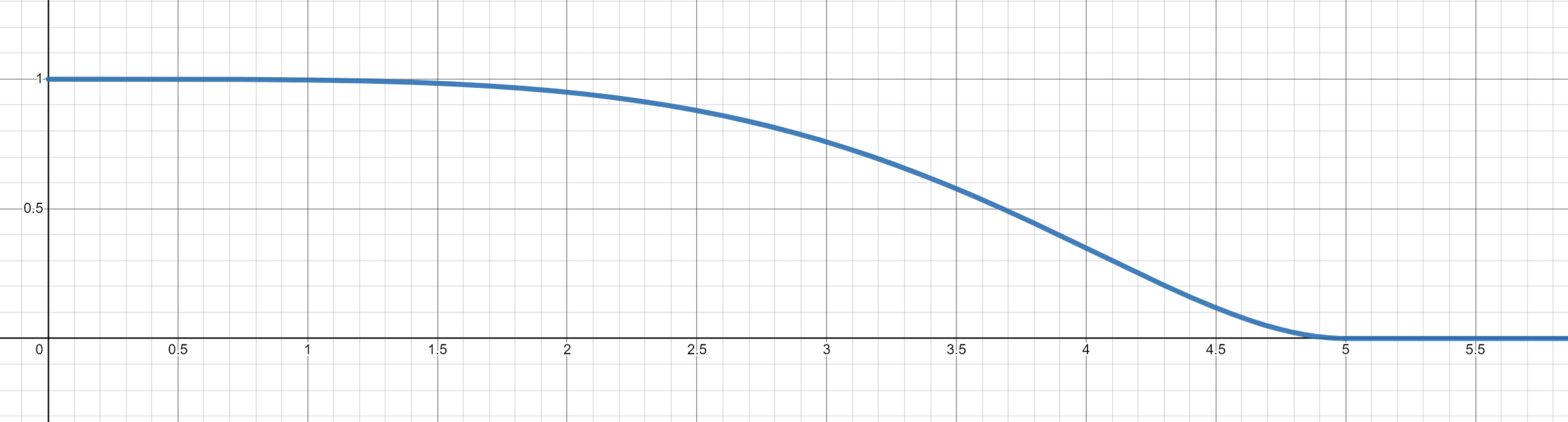
横軸が0のとき縦軸が1で、横軸の値が増加するにつれてスムーズに縦軸の値が下がっていき、横軸が閾値(5)のとき縦軸が0になっています。
この関数をライトカラーに乗算してやれば閾値周辺がスムーズになりそうです。
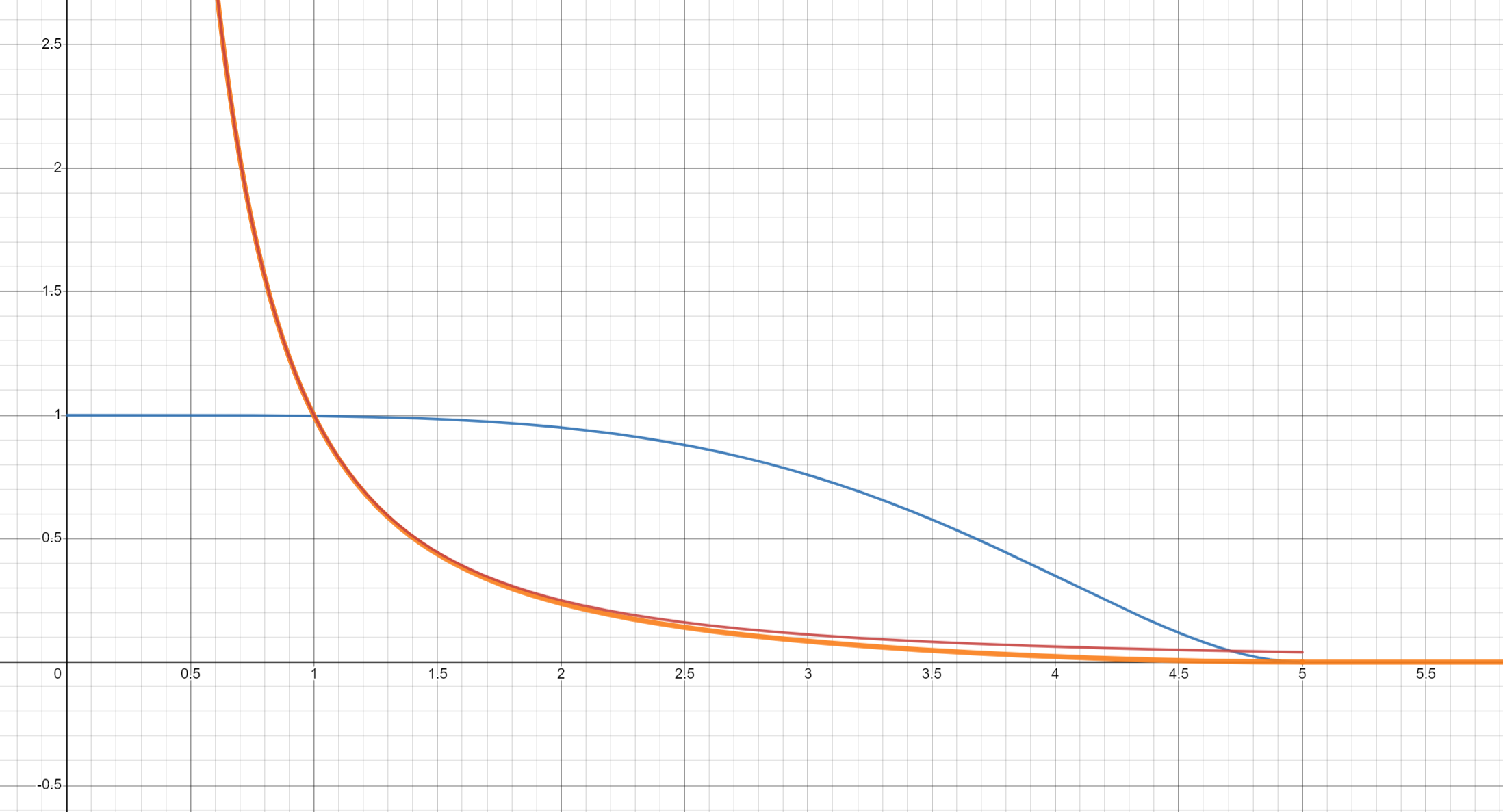 黄色の線が乗算したもの
黄色の線が乗算したもの
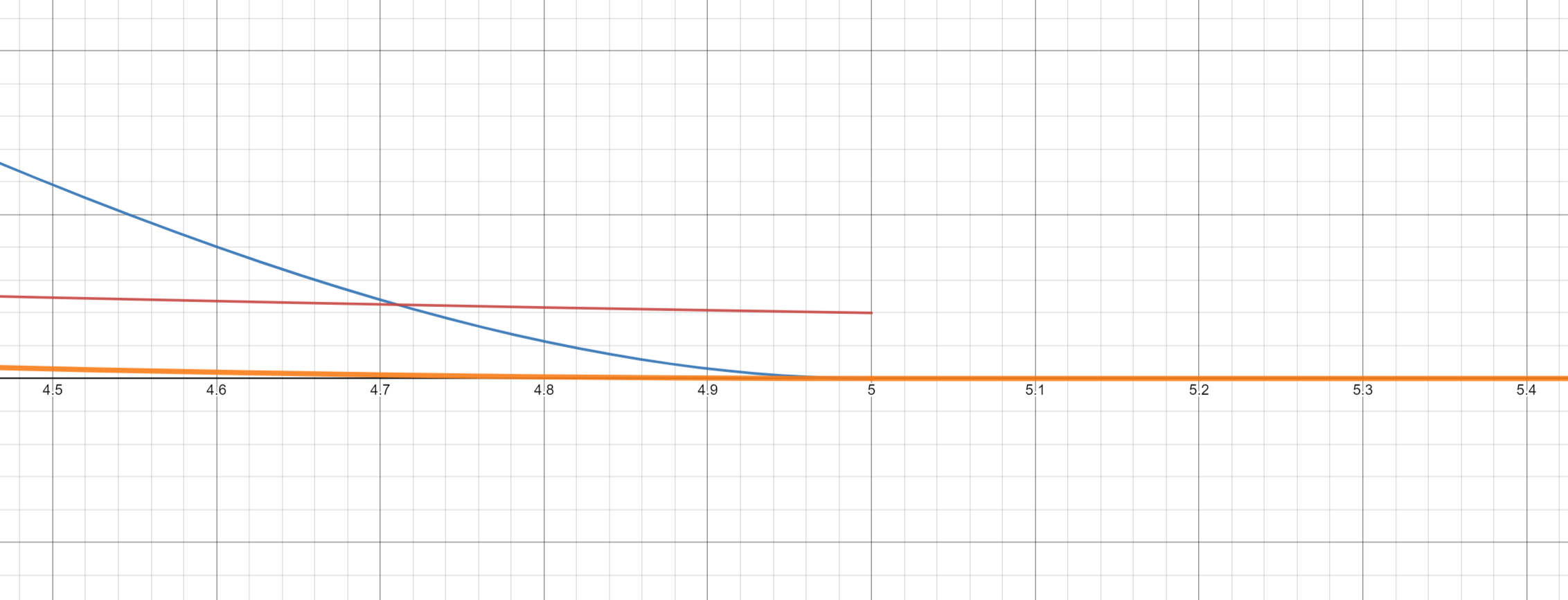 閾値(5)周辺を拡大
閾値(5)周辺を拡大
ちょっと見づらいですが、ライトカラー(赤線)に先程の青線のグラフを乗算すると、閾値周辺でスムーズに0になっていることがわかります。
この青線のグラフはReal Shading in Unreal Engine 4に掲載された関数を使用しています。
| 記号 | 説明 |
|---|---|
| ライトからの距離 | |
| ライトが届く距離(閾値) | |
|
|
こちらの関数を使って減衰をスムーズにしたものが以下になります。
 エッジ部分がスムーズに暗くなっている
エッジ部分がスムーズに暗くなっている
これで光が届く限界距離を実装することができ、ライトカリングができるようになりました。
…と言ったところで申し訳ないのですが、ここまでの議論ではライトカリングができるようになっただけであり、実際にライトカリングを実現するには「光が届いていないところは描画しない」というカリング処理を実装してやらないといけません。CPU側で各オブジェクトに対してライトが届くかどうかを判定し、届いていなければ描画処理自体をしないという処理にします。この実装については本記事では扱いませんので、ご注意ください。
ポイントライトの実装
ここまででポイントライトを実装するために必要な情報は出揃いました。一度整理してみます
| 設定 | 値の形式 | 備考 |
|---|---|---|
| ライト位置 | ベクトル | ライト方向、減衰の計算のために必要 |
| ライトが届く距離(閾値) | スカラー | ライトカリングのために必要 |
| ライトカラー | ベクトル(RGB) | |
| ライト強度 | スカラー |
これらはコンスタントバッファで用意します
cbuffer CbLight : register(b1)
{
float3 LightPosition : packoffset(c0); // ライト位置
float LightInvSqrRadius : packoffset(c0.w); // ライトが届く距離(2乗の逆数)
float3 LightColor : packoffset(c1); // ライトカラー
float LightIntensity : packoffset(c1.w); // ライト強度
}
ライトが届く距離について、「2乗の逆数」となっていますが、これは計算処理負荷を下げるためにやっていることです。CPU側で2乗の逆数を計算しておきコンスタントバッファに書き込みます。
(3)の式の実装は次のとおりです
float SmoothDistanceAttenuation
(
float squareDistance, // ライトからの距離の2乗
float invSqrAttRadius // ライトが届く距離の2乗の逆数
)
{
float factor = squareDistance * invSqrAttRadius;
float smoothFactor = saturate(1.0f - factor * factor);
return smoothFactor * smoothFactor;
}
距離減衰の実装は以下のとおりです
#define MIN_DIST (0.01)
float GetDistanceAttenuation
(
float3 unnormalizedLightVector, // ライト位置とピクセル位置の差分
float invSqrAttRadius // ライトが届く距離の2乗の逆数
)
{
float sqrDist = dot(unnormalizedLightVector, unnormalizedLightVector);
float attenuation = 1.0f / (max(sqrDist, MIN_DIST * MIN_DIST));
attenuation *= SmoothDistanceAttenuation(sqrDist, invSqrAttRadius);
return attenuation;
}
以上の関数を利用し、ポイントライトを実装します
float3 EvaluatePointLight(
float3 surfacePosition, // ピクセル位置
float3 lightPositon, // ライト位置
float3 lightColor, // ライトカラー
float lightIntensity, // ライト強度
float lightInvSqrRadius // ライトが届く距離の2乗の逆数
)
{
float att = GetDistanceAttenuation(
lightPositon - surfacePosition,
LightInvSqrRadius);
return lightColor * lightIntensity * att;
}
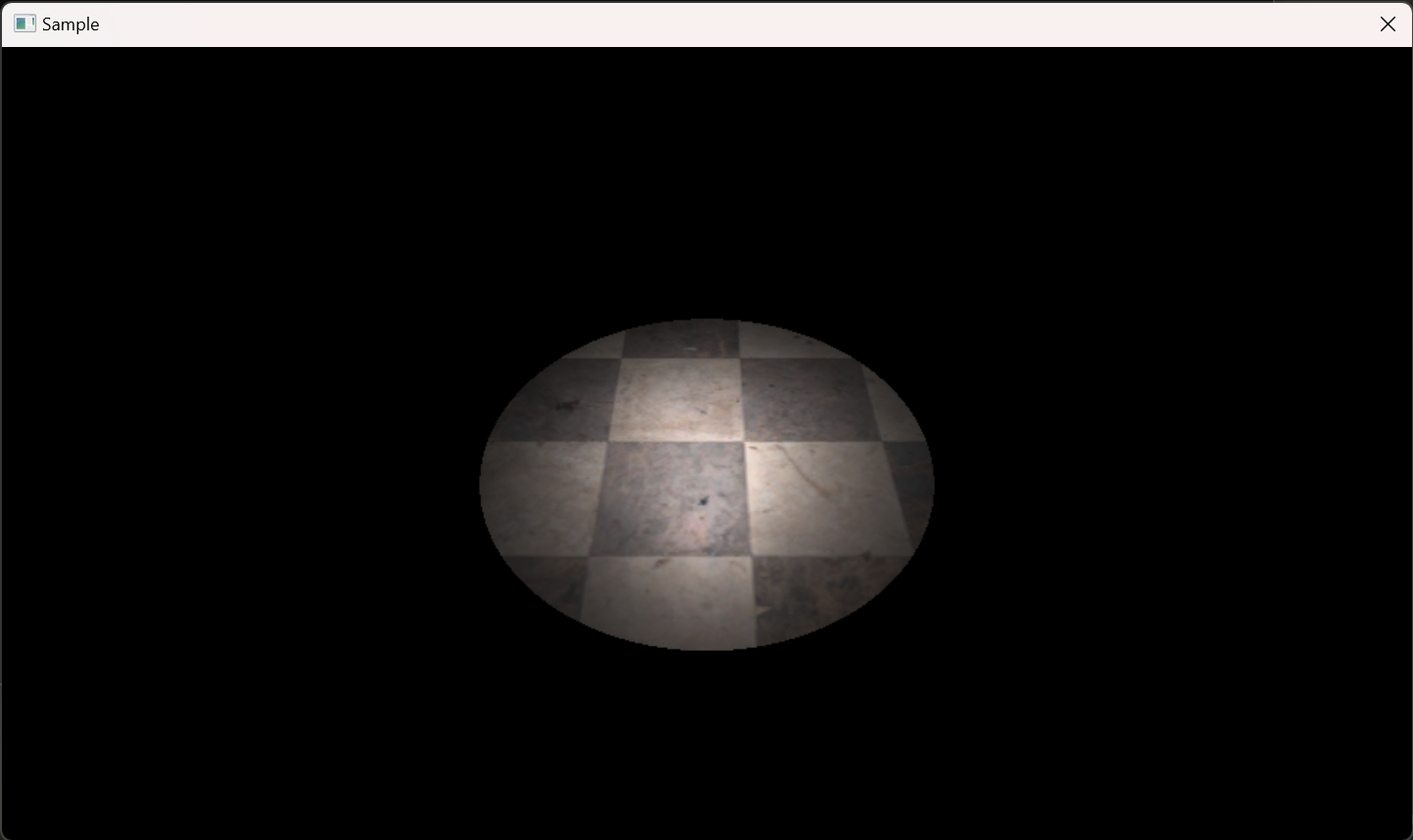
スポットライト
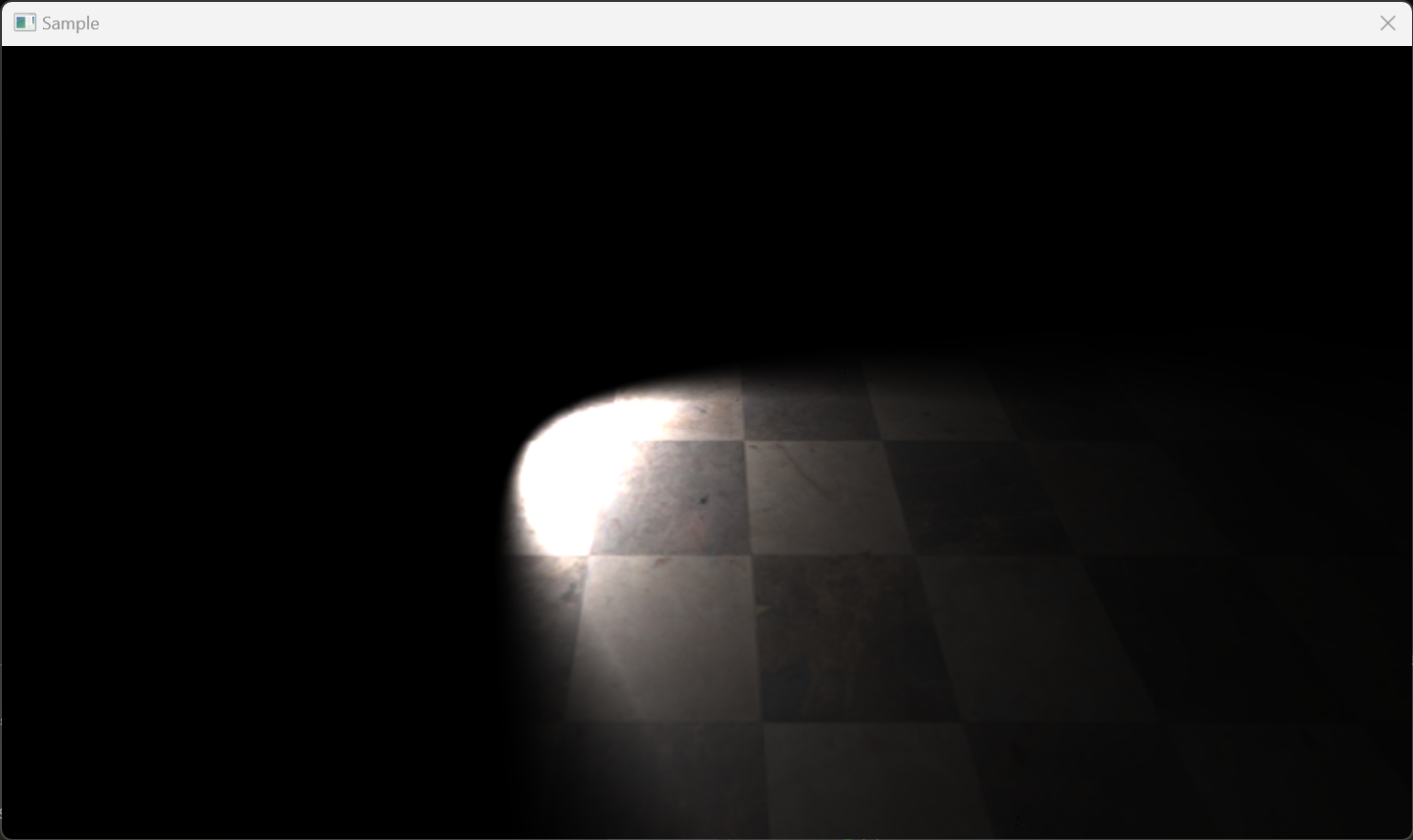 スポットライトの例。効果がわかりやすいようライトを傾けた状態
スポットライトの例。効果がわかりやすいようライトを傾けた状態
ポイントライトは光源の位置から光が球状広がっていきます。これに対し、スポットライトは光源の位置から円錐上に広がっていきます。
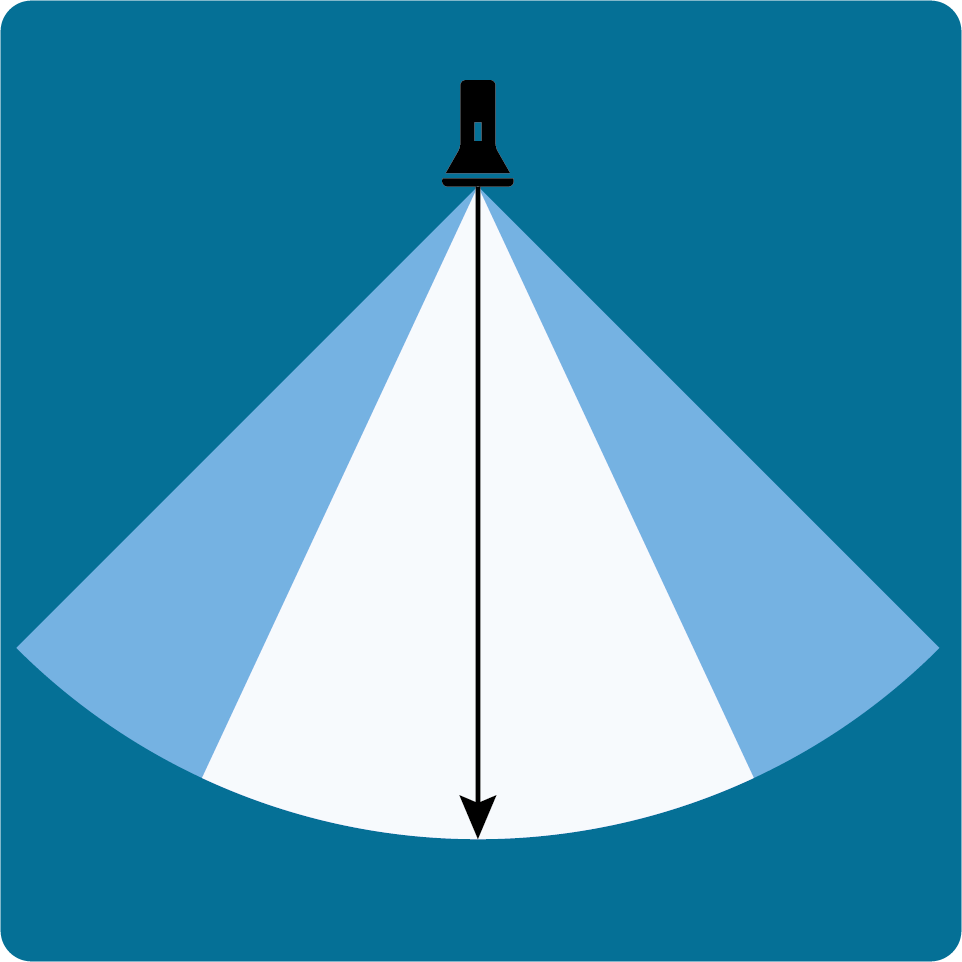 スポットライトの概念図。2Dで表現しているので扇形になっているが、3D空間上では円錐形になる
スポットライトの概念図。2Dで表現しているので扇形になっているが、3D空間上では円錐形になる
距離による減衰(スポットライト)
距離による減衰はスポットライトでも起こります。厳密にはスポットライトの立体角を用いて減衰を計算するのですが、今回は簡単化のために、ポイントライトと同じ減衰計算を使うこととします。イメージとしてはポイントライトの周囲に穴をあけた球体状の覆いを配置しているようなものでしょうか?
角度による減衰
スポットライトではライト方向と照射位置-光源位置の角度によって光の減衰が起こります。ひとまず下図を確認してください。
| 記号 | 説明 |
|---|---|
| ライトの向きベクトル | |
| 光源ベクトルの逆向きのベクトル | |
|
|
|
| 角度減衰が起こらない範囲を表す角 | |
| ライトが当たる範囲を表す角 |
図中のベクトルは全て単位ベクトルです。
光源ベクトルは照射位置から光源の方向を正とするので、
角度による減衰は
これだけだと分かりづらいかもしれないので、実際にスポットライトを使った画像を示します。
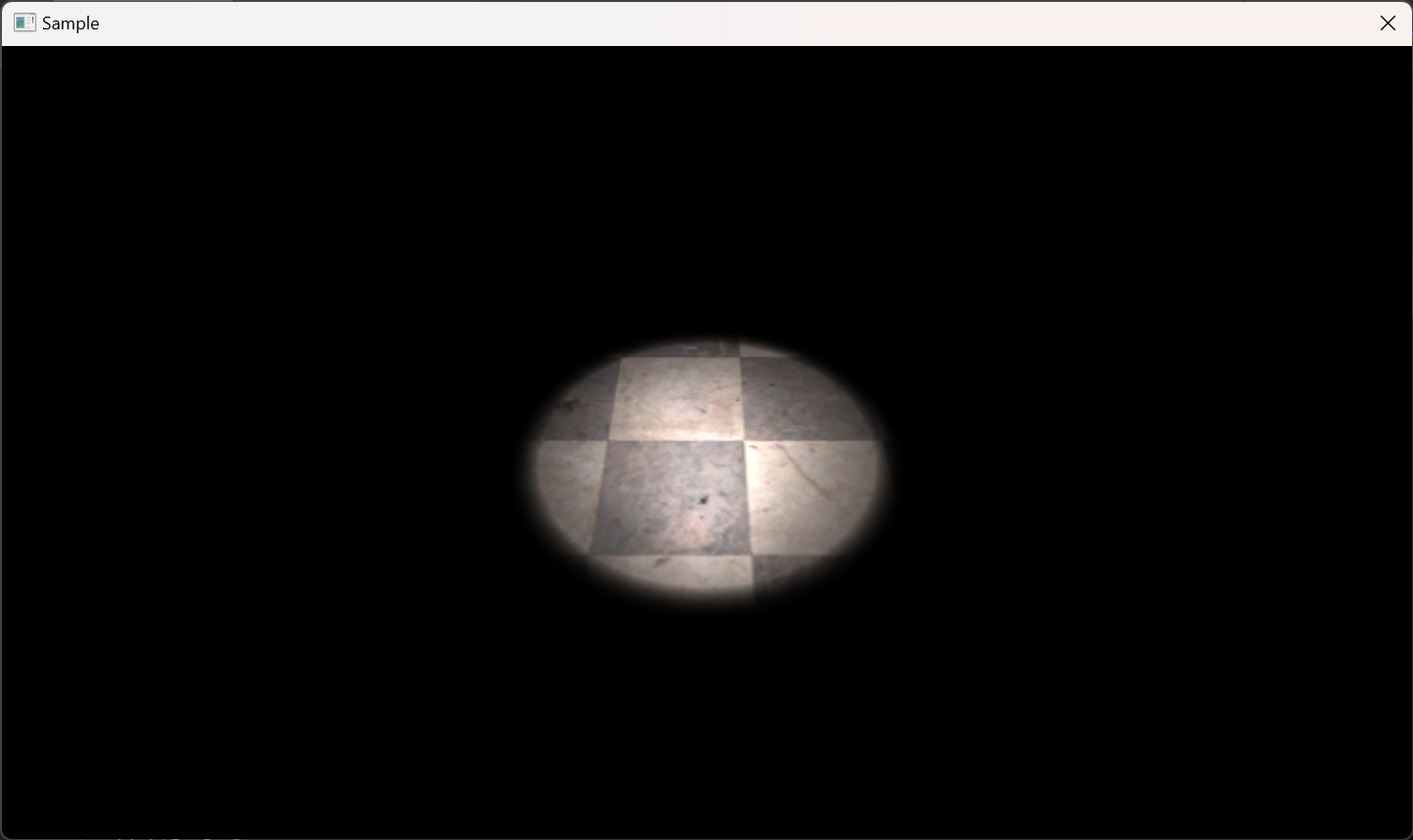
こちらは
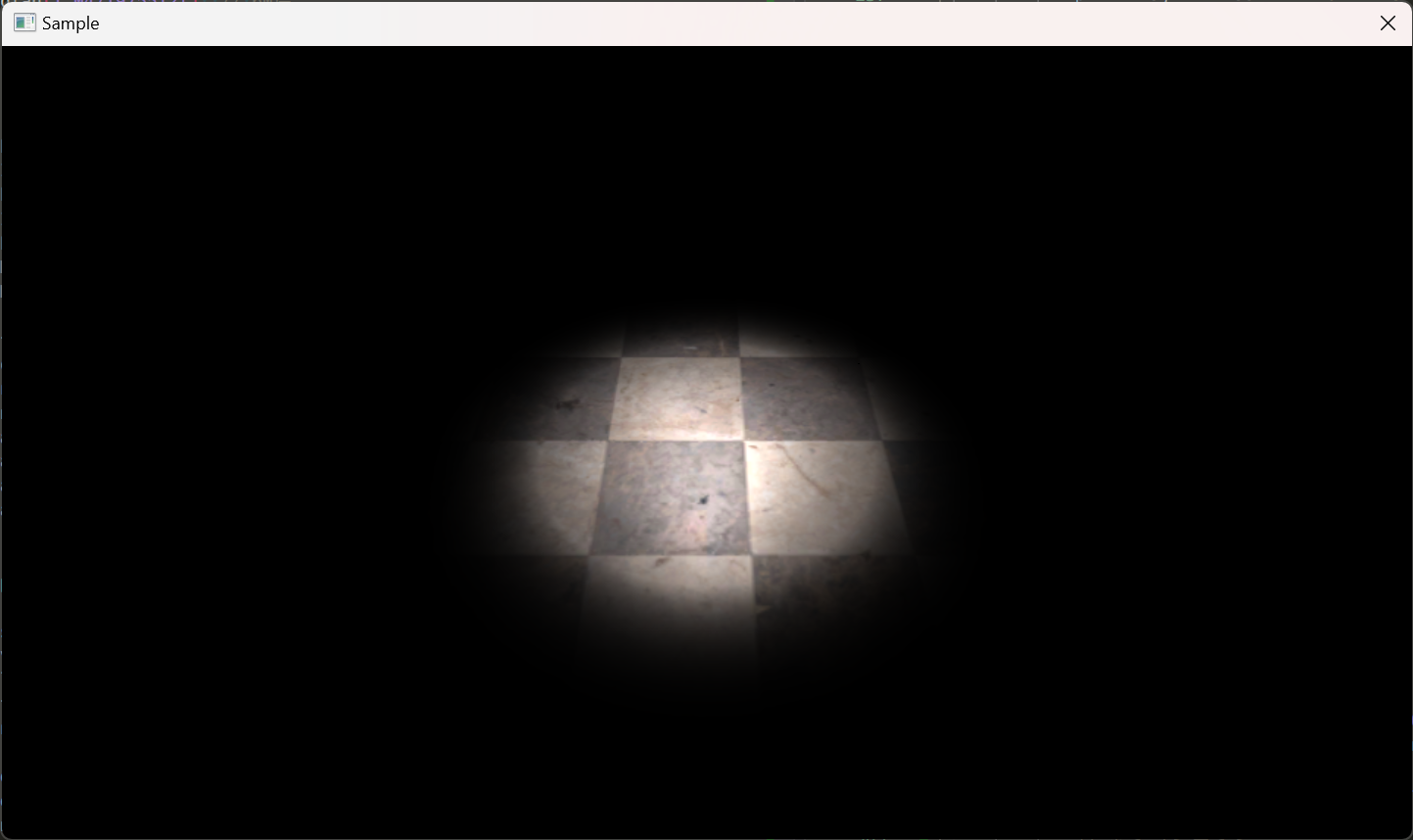
こちらは
この減衰を表す式は以下のとおりです。リアルタイムレンダリング第4版の5.2を参考にしました。
この式をそのまま実装すると、max(cos_p - cos_u, 0.01)のような形式にします。
スポットライトの実装
それではスポットライトの実装に移ります。まずは必要な情報をまとめます。
| 設定 | 値の形式 | 備考 |
|---|---|---|
| ライト位置 | ベクトル | ライト方向、減衰の計算のために必要 |
| ライトが届く距離(閾値) | スカラー | ライトカリングのために必要 |
| ライトカラー | ベクトル(RGB) | |
| ライト強度 | スカラー | |
| ライトの向き | ベクトル | 角度減衰の計算のために必要 |
| 角度減衰が起こらない範囲を表す角 | スカラー | 角度減衰の計算のために必要 |
| ライトが当たる範囲を表す角 | スカラー | 角度減衰の計算のために必要 |
角度減衰の実装は以下のとおりです。
#define MIN_DIST (0.01)
float GetAngleAttenuation
(
float cos_s, // ライト方向ベクトルと光源ベクトルの内積
float cos_p, // 内側角のcos
float cos_u // 外側角のcos
)
{
float d = max(cos_p - cos_u, MIN_DIST);
float t = saturate((cos_s - cos_u) / d);
return t * t;
}
スポットライトの実装は以下のとおりです。
距離減衰については、ポイントライトの距離減衰の実装を参照してください
float3 EvaluateSpotLight
(
float3 worldPos, // ピクセル位置
float3 lightPos, // ライト位置
float lightInvRadiusSq, // ライトが届く距離の二乗の逆数
float3 lightForward, // ライトの向き
float3 lightColor, // ライトカラー
float lightIntensity, // ライト強度
float lightInnerCos, // 角度減衰が起こらない範囲を表す角
float lightOuterCos // ライトが当たる範囲を表す角
)
{
float3 unnnormalizedLightVector = lightPos - worldPos;
float3 L = normalize(unnnormalizedLightVector);
float att = GetAngleAttenuation(dot(-L, lightForward), lightInnerCos, lightOuterCos);
att *= GetDistanceAttenuation(unnnormalizedLightVector, lightInvRadiusSq);
return lightColor * lightIntensity * att;
}
最終的に出力するカラー
最後に、BRDFと合わせて最終的なカラーを出力するコードを載せておきます。ただし、一部の記述を省略していますのでご注意ください。
BRDFについては前回の記事を参照してください。
// ライトカラー
float3 lit = float3(1.0, 1.0, 1.0);
// ディレクショナルライトの場合
lit = EvaluateDirectionalLight(...);
// ポイントライトの場合
lit = EvaluatePointLight(...);
// スポットライトの場合
lit = EvaluateSpotLight(...)
// 出力カラー
float3 outputColor = saturate(dot(N, L)) * BRDF * lit;
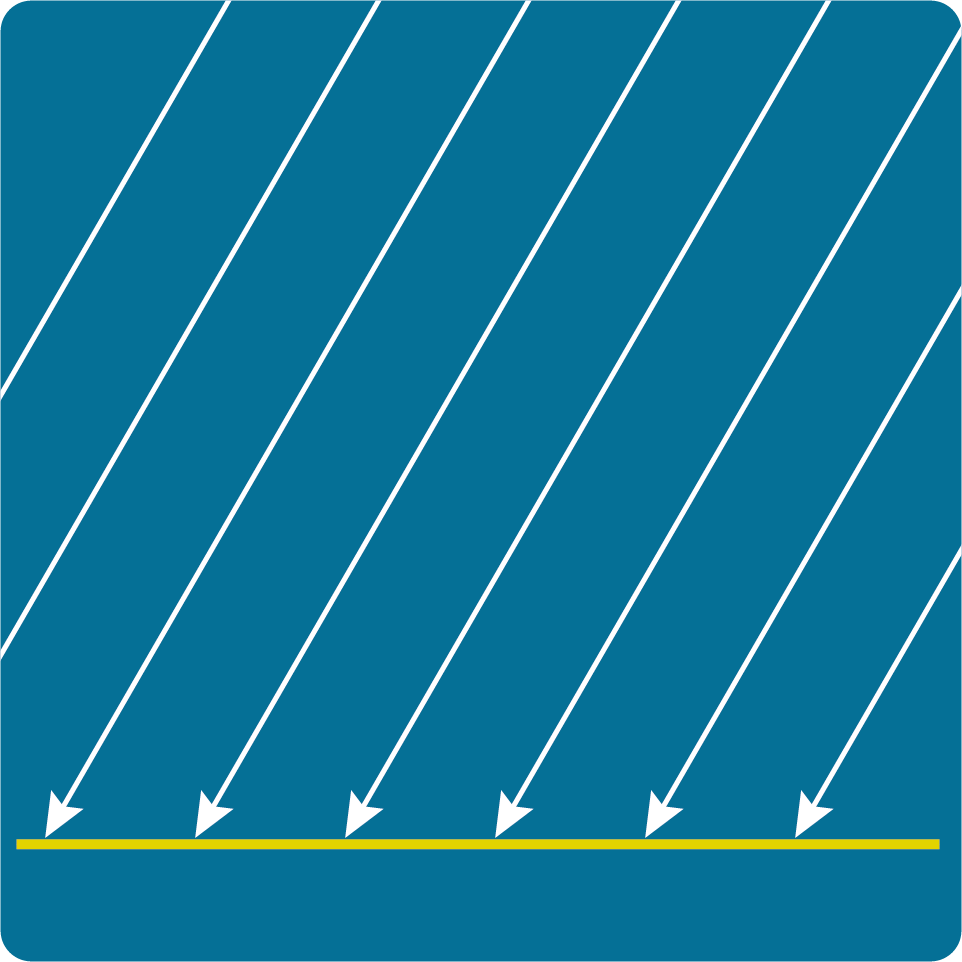
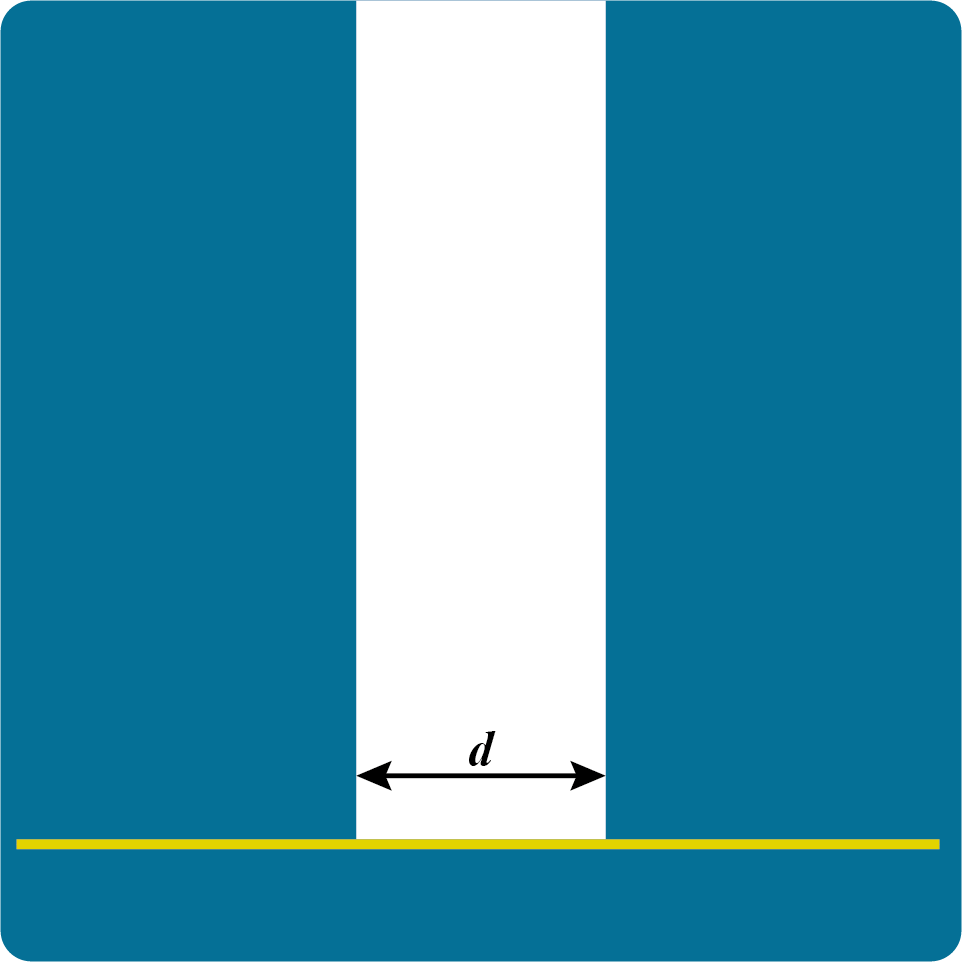 上からディレクショナルライトが当たっている様子
上からディレクショナルライトが当たっている様子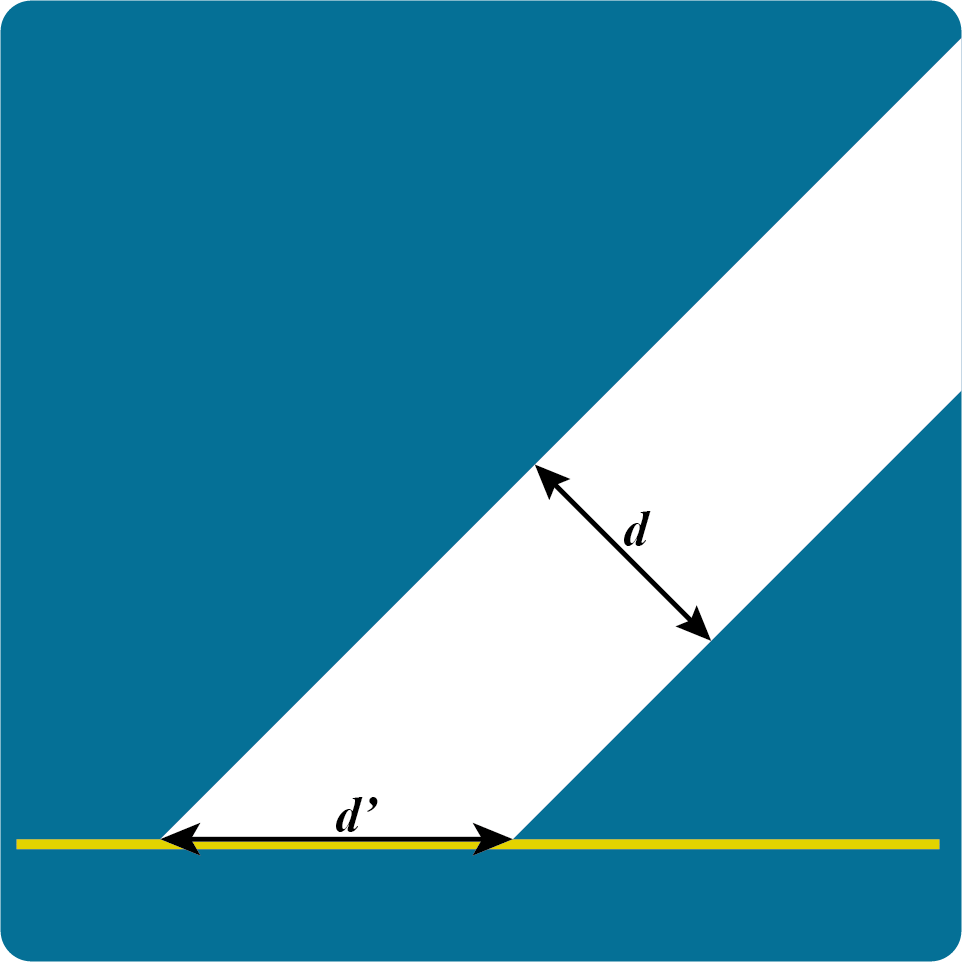 ライトを傾けた図。照射範囲が少し広くなる
ライトを傾けた図。照射範囲が少し広くなる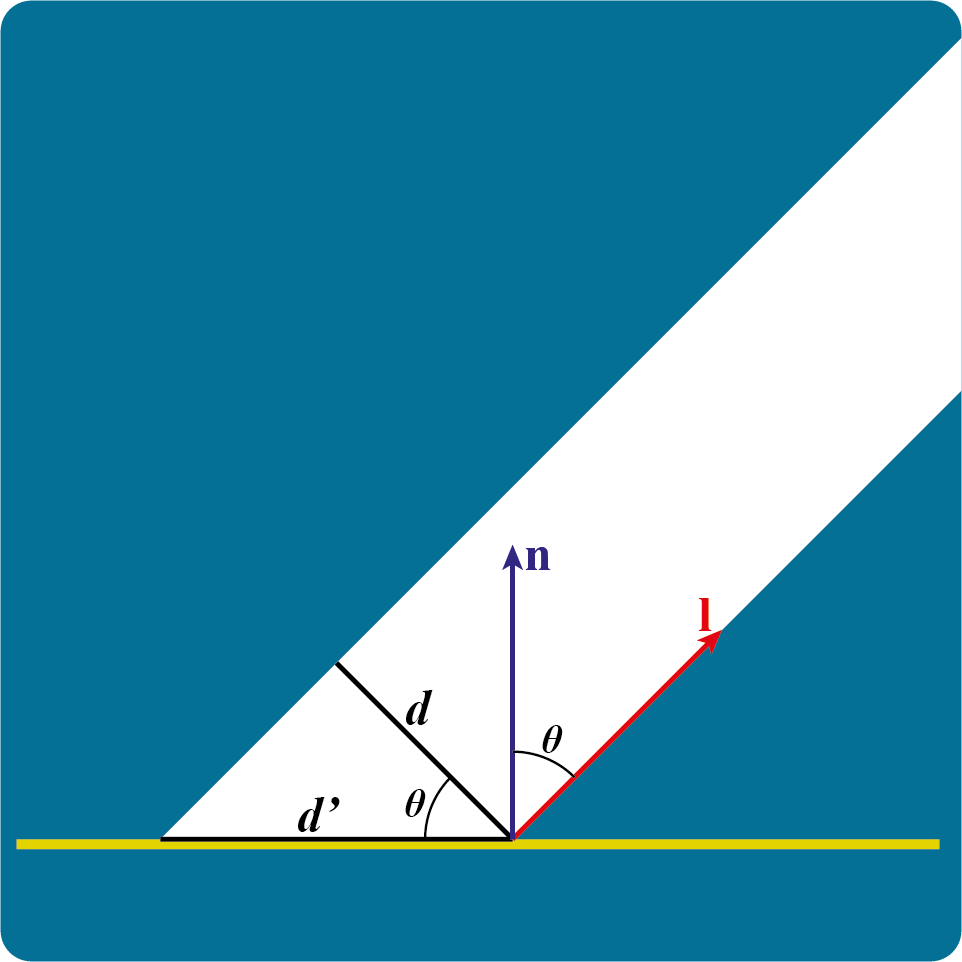
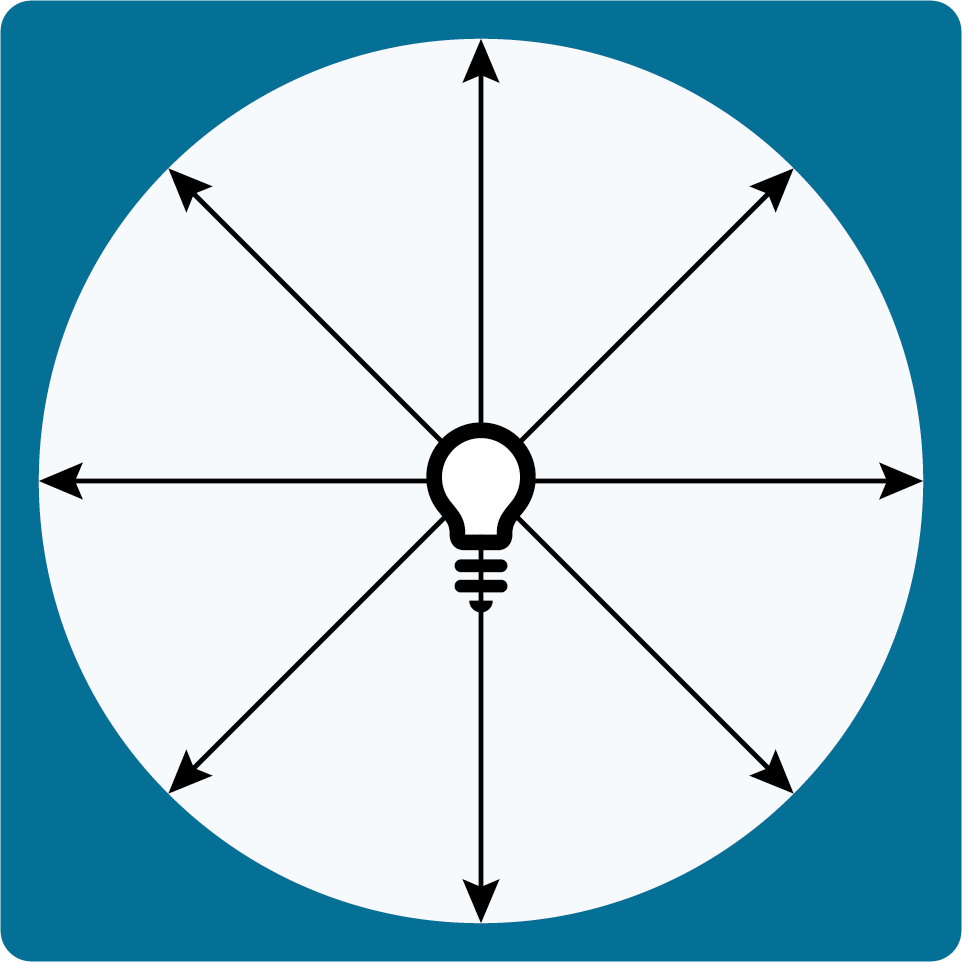
 今回のスポットライトのイメージ
今回のスポットライトのイメージ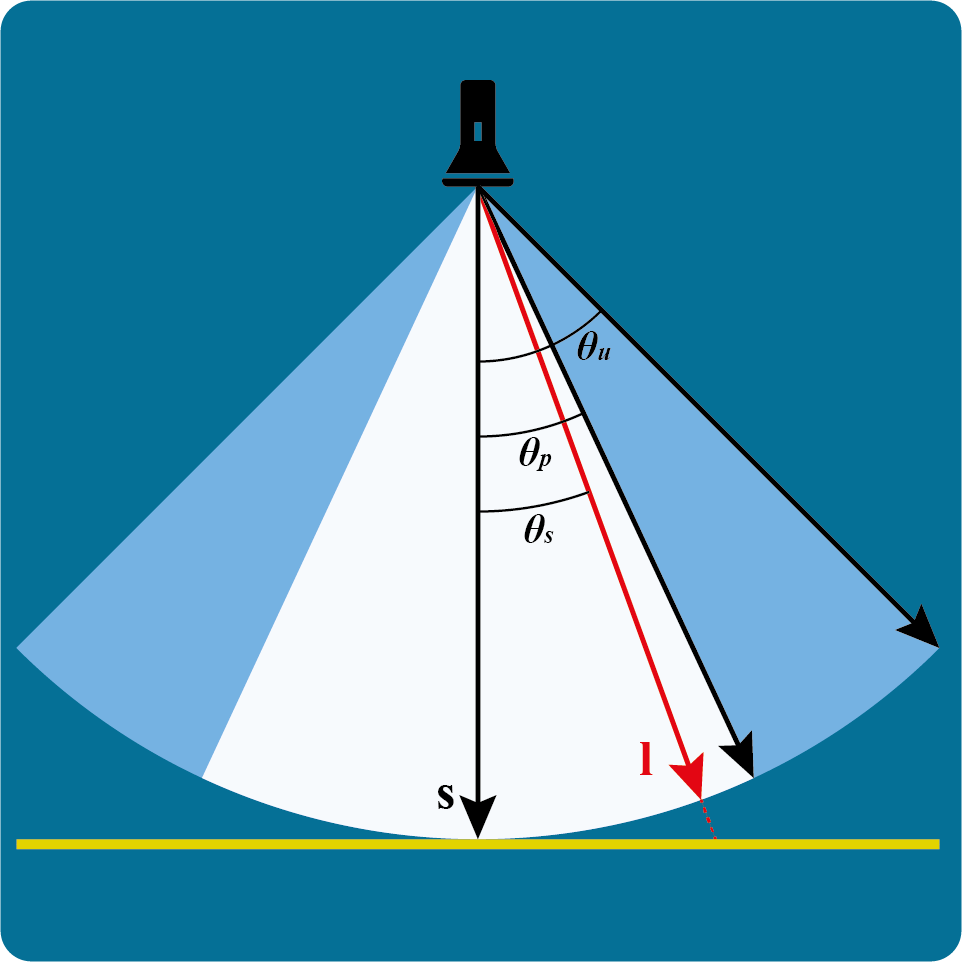 スポットライトの概念図
スポットライトの概念図
Discussion