AHC055 参加記

AHC055 参加記

76位、perf.2178 の解法です。

解法

貪欲法です。山登り、焼きなましやビームサーチは一切使っていません。

1. Hが最も小さい箱を選び、素手で破壊し武器を取り出します
2. 取り出した武器を評価値（後述）の大きい箱順に使います
3. 新しく武器を手に入れたら2に戻ります
4. 手持ちの武器がなくなったら1に戻ります
5. これを箱がなくなるまで繰り返します

この解法のポイントは2における評価値の定義です。

評価値の定義

まずは武器 $wi$ を持っている時、まだ開いていない箱 $ti$ に対して次のように評価値 $S(ti)$を定めました。

$$S(ti) = \min(H_{ti},A_{wi,ti})$$

意味としては、「今持っている武器 $wi$ を箱 $ti$ に使うときに与えられるダメージ量」です。なるべく大きなダメージを与えられる方が良いので、残っている箱の中でこの評価値が最も大きいものを攻撃しました。

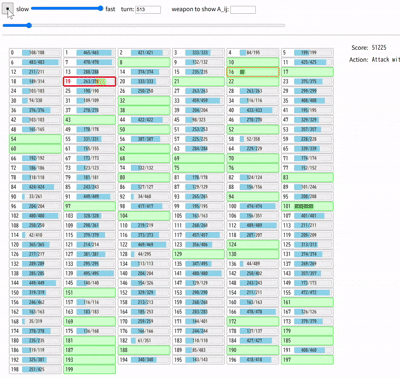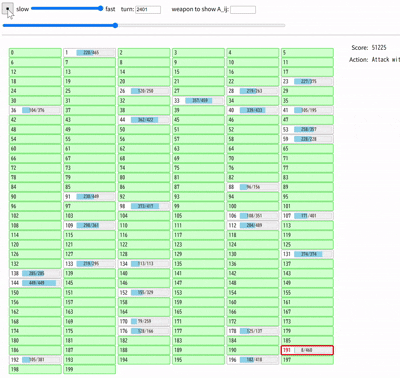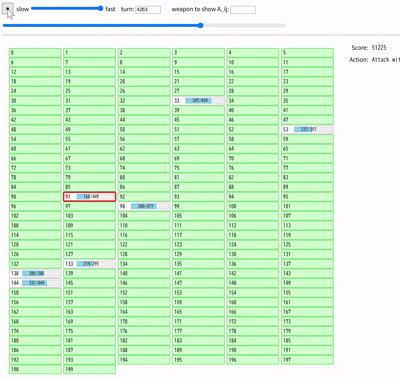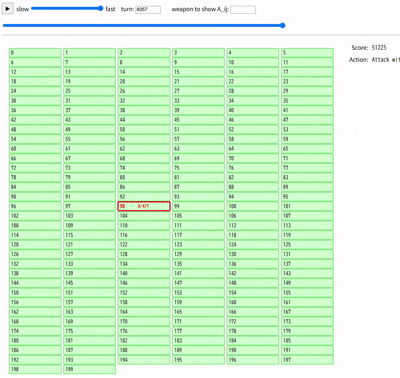
これでも悪くは無いのですが、最後に残る宝箱を全て素手で壊している点が気になります。最後に残る宝箱にはどのような特徴があるか考えた結果、宝箱のインデックスを $ti$ として $\sum_{i}A_{i,ti}$ が小さい宝箱ほど最後に残り、素手で壊される傾向がありました。この値が小さいというのは、この宝箱に対して有効な武器が少ないということを意味するので、攻撃先として狙われにくくなるようです。

そこで、評価値を改めて以下のように定義しました。
ただし、評価値の計算時点で残っている武器の集合を $B$ としています。

$$S(ti) = \min(H_{ti},A_{wi,ti}-(\sum_{i \in B}A_{i,ti})/D)$$

ここで、$D$ は適当な定数です。
$\sum_{i}A_{i,ti}$ が小さいような宝箱 $ti$ ほど狙われやすくして、最後に残るのを防ぎました。
このような工夫をすると最後に残された宝箱を素手で壊す時間が減り、スコアが格段に上がりました。

ここから色々と改善して、最終的には以下の定義になりました。

$$S(ti) = \min(H_{ti},A_{wi,ti}-(\sum_{i \in B}C_iA_{i,ti}^2)/D)$$

また、評価値の最も大きいものを選ぶ代わりに一定確率で2番目のものを選んだり、$D$ を乱数にすることでランダム性を加えました。そして、時間いっぱい解を作って最も良いものを出力しました。

もっともスコアが高かった提出

感想

長期コンでも結果が出せるように精進を続けたいです。