WebXRはどうやって左右の視野毎に描画しているのか？

WebXRは左右の視野毎に別々に描画を行っているが、具体的にはどのように処理しているのかコードを通して理解をしたい。
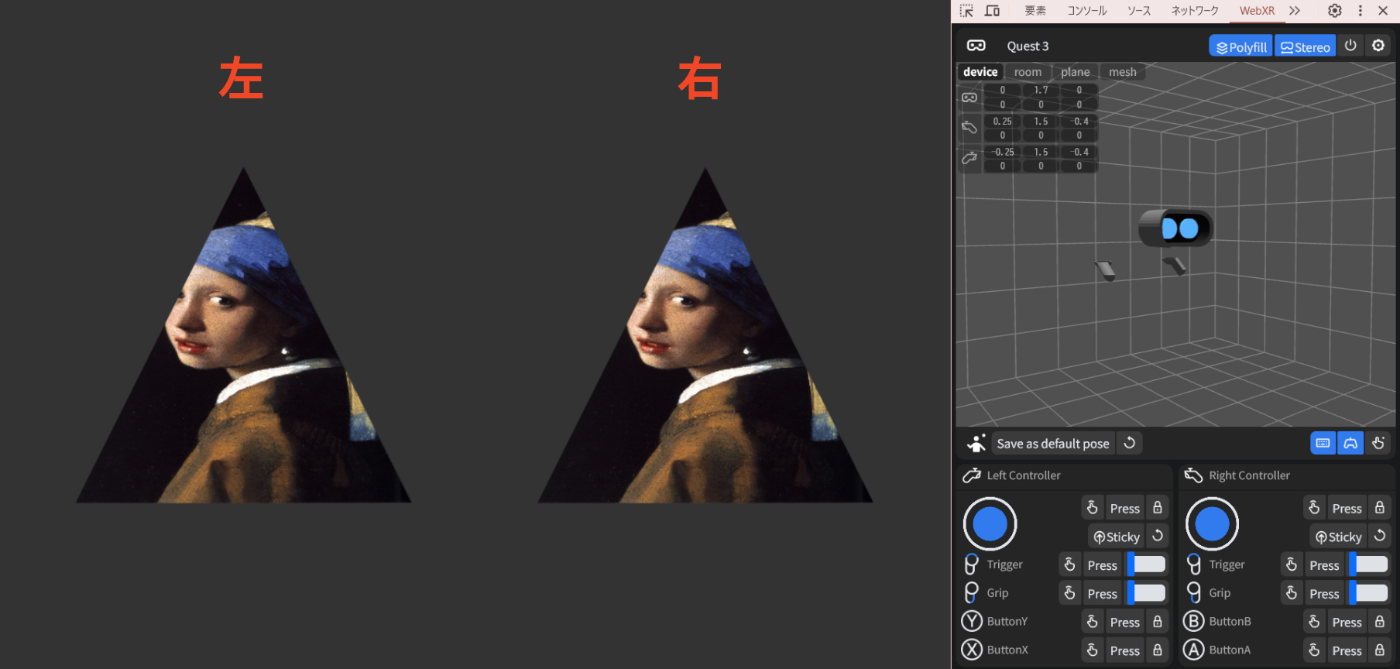
↓Meta Quest 3 でのキャプチャ動画

https://youtu.be/YAaHlUCExV4

appendChild

今回のコード一式

appendChild

シェーダーコード

const vsSource = `
  attribute vec3 aPosition;
  attribute vec2 aTexCoord;  // テクスチャ座標
  uniform mat4 uProjectionMatrix;
  uniform mat4 uViewMatrix;
  uniform mat4 uModelMatrix;
  varying vec2 vTexCoord;    // フラグメントシェーダーに渡すテクスチャ座標
  void main(void) {
    gl_Position = uProjectionMatrix * uViewMatrix * uModelMatrix * vec4(aPosition, 1.0);
    vTexCoord = aTexCoord;
  }
`;

const fsSource = `
  precision mediump float;
  uniform sampler2D uTexture;  // テクスチャサンプラー
  varying vec2 vTexCoord;
  void main(void) {
    gl_FragColor = texture2D(uTexture, vTexCoord);
  }
`;

`gl_Position = uProjectionMatrix * uViewMatrix * uModelMatrix * vec4(aPosition, 1.0);` がなにをしているのかの図解

appendChild

レンダー処理

/**
 * XR フレームごとのレンダリング処理
 * @param time 現在のタイムスタンプ
 * @param frame 現在の XR フレーム
 */
function onXRFrame(time: number, frame: XRFrame) {
  const session = frame.session;
  const baseLayer = session.renderState.baseLayer;
  if (!baseLayer) return;

  session.requestAnimationFrame(onXRFrame);

  // ユーザーの位置・向きを取得
  const pose = frame.getViewerPose(xrRefSpace);
  if (!pose) return;

  // XRWebGLLayer のフレームバッファをバインド
  gl.bindFramebuffer(gl.FRAMEBUFFER, baseLayer.framebuffer);
  gl.clearColor(0.2, 0.2, 0.2, 1.0);
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  // シェーダープログラムの利用開始
  gl.useProgram(shaderProgram);

  // シェーダー内の attribute と uniform のロケーションを取得
  const posLoc = gl.getAttribLocation(shaderProgram, 'aPosition');
  const texCoordLoc = gl.getAttribLocation(shaderProgram, 'aTexCoord');
  const projLoc = gl.getUniformLocation(shaderProgram, 'uProjectionMatrix');
  const viewLoc = gl.getUniformLocation(shaderProgram, 'uViewMatrix');
  const modelLoc = gl.getUniformLocation(shaderProgram, 'uModelMatrix');
  const textureLoc = gl.getUniformLocation(shaderProgram, 'uTexture');

  // モデル行列を作成
  const modelMatrix = new Float32Array([
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, 0,
    0, 0, -1, 1  // Z軸を-1に移動
  ]);

  // 頂点バッファをバインドし、頂点属性を設定
  gl.bindBuffer(gl.ARRAY_BUFFER, buffers!.vertexBuffer);
  gl.enableVertexAttribArray(posLoc);
  gl.vertexAttribPointer(posLoc, 3, gl.FLOAT, false, 0, 0);

  // テクスチャ座標バッファをバインドし、テクスチャ座標を設定
  gl.bindBuffer(gl.ARRAY_BUFFER, buffers!.texCoordBuffer);
  gl.enableVertexAttribArray(texCoordLoc);
  gl.vertexAttribPointer(texCoordLoc, 2, gl.FLOAT, false, 0, 0);

  // 各ビュー（左右の目）の描画処理
  for (const view of pose.views) {
    const viewport = baseLayer.getViewport(view);
    if (!viewport) return;
    
    gl.viewport(viewport.x, viewport.y, viewport.width, viewport.height);

    // 各ビューに対して射影行列とビュー行列をシェーダーに送信
    gl.uniformMatrix4fv(projLoc, false, view.projectionMatrix);
    gl.uniformMatrix4fv(viewLoc, false, view.transform.inverse.matrix);
    gl.uniformMatrix4fv(modelLoc, false, modelMatrix);

    // テクスチャをシェーダーに送信
    gl.activeTexture(gl.TEXTURE0);
    gl.bindTexture(gl.TEXTURE_2D, texture);
    gl.uniform1i(textureLoc, 0);

    // 三角形を描画
    gl.drawArrays(gl.TRIANGLES, 0, vertexCount);
  }
}

フローチャート

appendChild

こんな感じに描画される
※PCでのデバッグ用に Immersive Web Emulator を使っています。

appendChild

試しに view.eye === 'left' の場合は処理を飛ばしたらこうなった

   for (const view of pose.views) {
     const viewport = baseLayer.getViewport(view);
     if (!viewport) return;
+
+    // 左目の場合は描画しない
+    if (view.eye === 'left') continue;
+
     gl.viewport(viewport.x, viewport.y, viewport.width, viewport.height);

appendChild

viewport がどんな値なのか調べてみた

    const {x, y, width, height} = viewport;
    console.dir({eye: view.eye, x, y, width, height});

こんな結果が返ってきた

{
  "eye": "left",
  "x": 0,
  "y": 0,
  "width": 521.5,
  "height": 738
}
{
  "eye": "right",
  "x": 521.5,
  "y": 0,
  "width": 521.5,
  "height": 738
}

↓どうやらこういうことらしい

appendChild

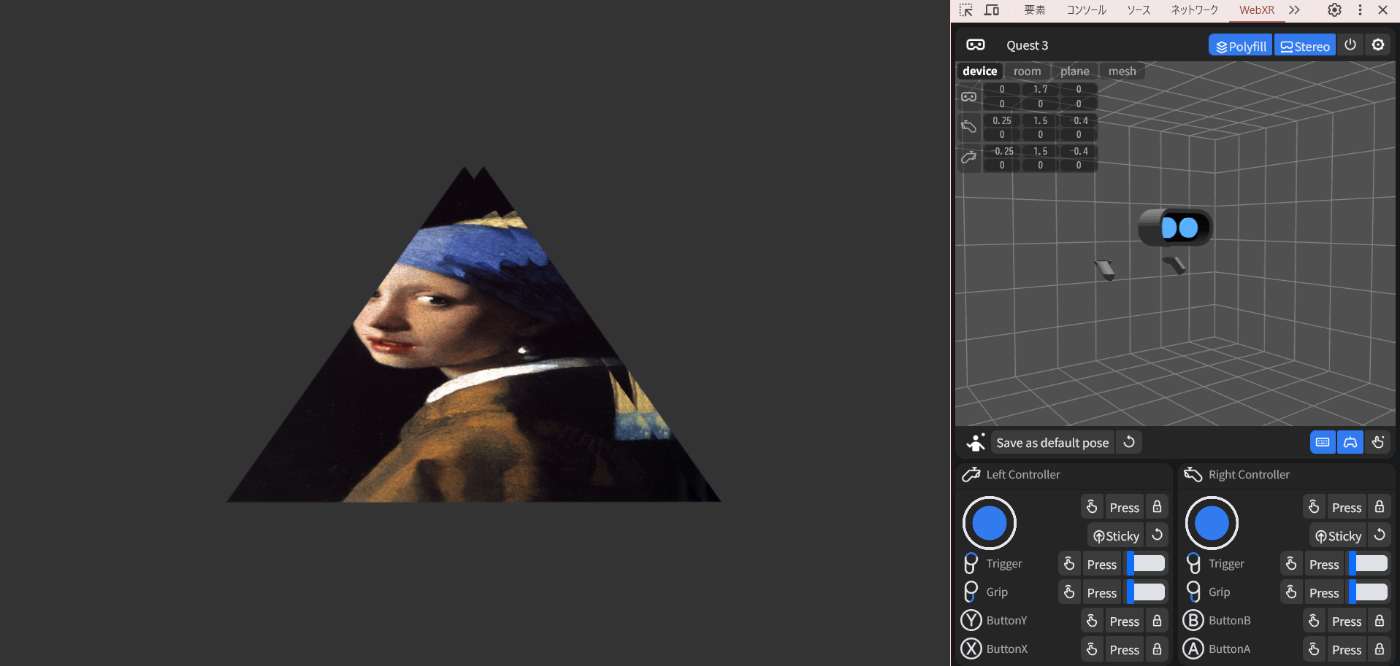
ちなみに左右に同じviewportを渡してみたらこうなった

-    gl.viewport(x, y, width, height);
+    gl.viewport(0, 0, width * 2, height);

↓左右の三角が平たくなって重なった

ちなみに、右が後から描画されているのでちょっと左にずれているのが右目用の三角形

appendChild

プロジェクション変換用の行列を単位行列にしてみたら、平たくなっていたのが直った

-    gl.uniformMatrix4fv(projLoc, false, view.projectionMatrix);
+    gl.uniformMatrix4fv(projLoc, false, [
+      1, 0, 0, 0,
+      0, 1, 0, 0,
+      0, 0, 1, 0,
+      0, 0, 0, 1
+    ]);

viewport の形状に合わせて座標を変換していたということっぽい。

appendChild

一旦プロジェクション用行列を元にもどす

-    gl.uniformMatrix4fv(projLoc, false, [
-      1, 0, 0, 0,
-      0, 1, 0, 0,
-      0, 0, 1, 0,
-      0, 0, 0, 1
-    ]);
+    gl.uniformMatrix4fv(projLoc, false, view.projectionMatrix);

appendChild

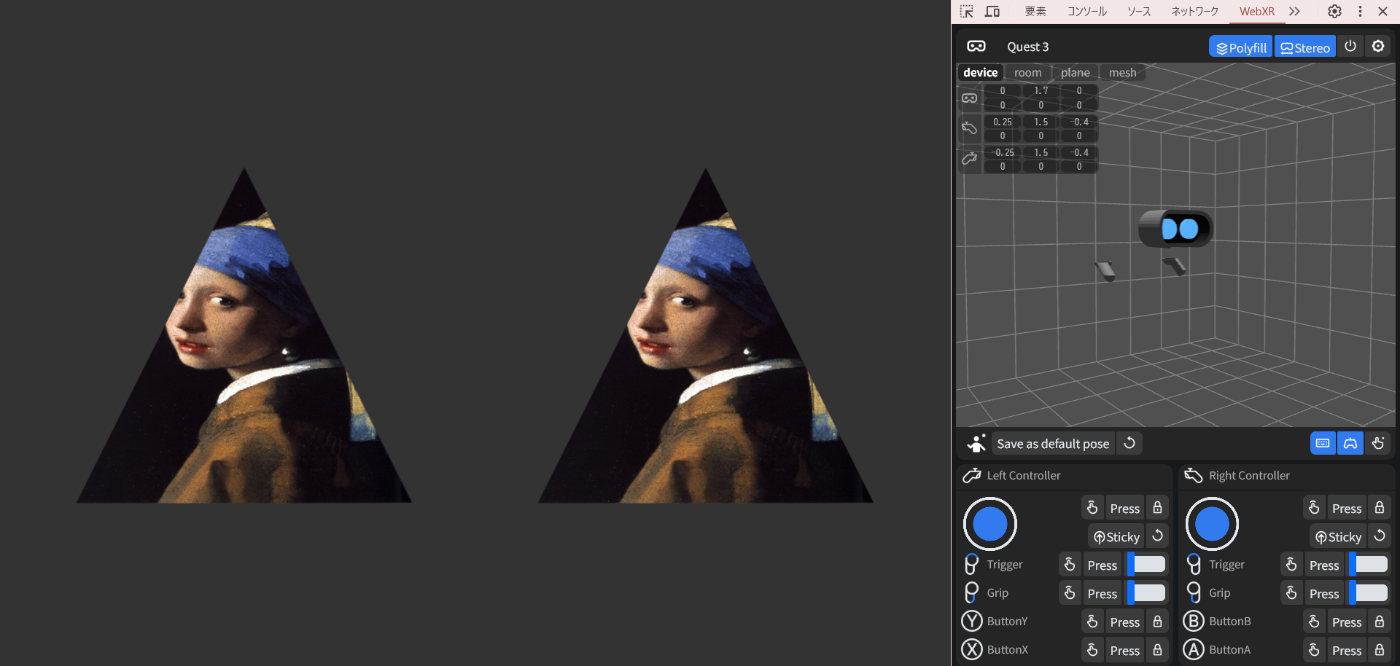
ビュー変換用に渡している行列が、具体的に左右でどう違うのかみてみる。

    console.log({
      eye: view.eye,
      viewLoc: view.transform.inverse.matrix,
    });

↓こんな結果になった

{
  "eye": "left",
  "viewLoc": {
    "0": 1,
    "1": 0,
    "2": 0,
    "3": 0,
    "4": 0,
    "5": 1,
    "6": 0,
    "7": 0,
    "8": 0,
    "9": 0,
    "10": 1,
    "11": 0,
    "12": 0.019999999552965164,
    "13": 0,
    "14": 0,
    "15": 1
  }
}
{
  "eye": "right",
  "viewLoc": {
    "0": 1,
    "1": 0,
    "2": 0,
    "3": 0,
    "4": 0,
    "5": 1,
    "6": 0,
    "7": 0,
    "8": 0,
    "9": 0,
    "10": 1,
    "11": 0,
    "12": -0.019999999552965164,
    "13": 0,
    "14": 0,
    "15": 1
  }
}

↓行列の表現にするとこう
左目:

\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0.019999999552965164 & 0 & 0 & 1 \end{pmatrix}

右目:

\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -0.019999999552965164 & 0 & 0 & 1 \end{pmatrix}

appendChild

これがどういうことなのか、ChatGPT o3-mini-high に聞いてみた
要約: 右目と左目の位置のずれ（約0.02 = 20cmずつ左右にずれている）
具体的には、以下のような意味があります。
4×4 行列とは？

3D 空間での変換（平行移動、回転、拡大縮小など）を一つの行列で表現するために、座標に 1 を付け加えた同次座標系を用います。

一般に、4×4 行列は
(a11a12a13a14a21a22a23a24a31a32a33a34a41a42a43a44)
   \begin{pmatrix}
   a_{11} & a_{12} & a_{13} & a_{14} \\
   a_{21} & a_{22} & a_{23} & a_{24} \\
   a_{31} & a_{32} & a_{33} & a_{34} \\
   a_{41} & a_{42} & a_{43} & a_{44}
   \end{pmatrix}
   ​a11​a21​a31​a41​​a12​a22​a32​a42​​a13​a23​a33​a43​​a14​a24​a34​a44​​​のように表され、

左上の 3×3 部分 は回転や拡大縮小などの線形変換を、

最後の列（または場合によっては最後の行）が平行移動を表します。
今回の行列の構成

JSON の数値は、通常「行優先（row-major order）」または「列優先（column-major order）」のどちらかの順序で並んでいますが、ここでは 4 行×4 列の行列として変換しています。

例えば、左目の行列は次のようになります。
(1000010000100.019999999552965164001)
   \begin{pmatrix}
   1 & 0 & 0 & 0 \\
   0 & 1 & 0 & 0 \\
   0 & 0 & 1 & 0 \\
   0.019999999552965164 & 0 & 0 & 1
   \end{pmatrix}
   ​1000.019999999552965164​0100​0010​0001​​この行列はほとんど単位行列ですが、最後の行の最初の要素（ここでは 0.02 近くの値）が、x 軸方向の平行移動を示しています。
左目と右目の違い

両方の行列は同じ形ですが、
左目の行列では x 軸方向の平行移動が +0.019999999552965164、
右目の行列では -0.019999999552965164 となっています。
これは、左右の目で視点が少しずれている（パララックス効果）ことを意味し、立体視（ステレオ視）のために左右で異なる映像を提供するための設定です。

つまり、各目に対してわずかに異なるカメラ位置（ここでは x 軸方向のずれ）が適用されることで、奥行きのある映像を生成できるのです。
まとめると、
行列は 3D 空間での変換を表すためのものであり、ここでは単位行列に平行移動の成分が追加されている。
左右の目では、x 軸方向の平行移動が逆方向になっているため、各目から見る視点が微妙に異なり、それによって立体的な映像が得られる。
このように、各行列がどのように視点の変換を定義しているかを理解することで、シーン内でのカメラの位置や向き、さらにはステレオ効果の仕組みが把握できます。

appendChild

ちなみに、Immersive Web Emulator でゴーグルのY座標（上下方向）を 2.0 にしてみたら、こんな行列が返ってきた


 左目(1000010000100.019999999552965164−0.4017812013626098601)
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0.019999999552965164 & -0.40178120136260986 & 0 & 1
\end{pmatrix}
​1000.019999999552965164​010−0.40178120136260986​0010​0001​​
 右目(100001000010−0.019999999552965164−0.4017812013626098601)
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
-0.019999999552965164 & -0.40178120136260986 & 0 & 1
\end{pmatrix}
​100−0.019999999552965164​010−0.40178120136260986​0010​0001​​

appendChild

Y座標を元の 1.6 にもどし、Z座標（奥行）を 1.0 にしてみたら


 左目 (eye: "left")(1000010000100.0199999995529651640−11)
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0.019999999552965164 & 0 & -1 & 1
\end{pmatrix}
​1000.019999999552965164​0100​001−1​0001​​
 右目(100001000010−0.0199999995529651640−11)
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
-0.019999999552965164 & 0 & -1 & 1
\end{pmatrix}
​100−0.019999999552965164​0100​001−1​0001​​

appendChild

要するにこういうことらしい

\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ X平行移動 & Y平行移動 & Z平行移動 & 1 \end{pmatrix}

appendChild

 おまけ：なぜビュー行列として view の変換行列の逆行列を渡している？これは、シェーダー内でオブジェクトをカメラ空間に変換するために、ビュー行列としてカメラの変換の逆行列を使っているからです。

 詳しい解説カメラの変換行列（view.transform）

カメラの位置や向きを定義する行列です。この行列は、カメラ自身がどの位置にあってどの方向を向いているかを示します。
ビュー行列の役割

シーン内の各オブジェクトの位置はワールド空間にあります。これをカメラから見た視点（カメラ空間）に変換するために、ビュー行列を使用します。

ここで大事なのは、カメラの変換行列が「カメラがワールド空間にどのように存在するか」を示しているのに対して、ビュー行列は「ワールド空間からカメラ空間へどのように変換するか」を定義する点です。
逆行列が必要な理由

ワールド空間からカメラ空間へ変換するためには、カメラの変換を「反転」させる必要があります。

つまり、カメラの変換行列の逆行列を取ることで、各頂点がカメラに対してどの位置にあるかを計算できるのです。

このため、
gl.uniformMatrix4fv(viewLoc, false, view.transform.inverse.matrix);
のように、カメラの変換の逆行列をシェーダーに渡しています。

 まとめ
カメラの変換行列は、カメラの位置と向きを示します。

ビュー行列は、ワールド空間の座標をカメラ空間に変換するためのもの。
この変換は、カメラの変換行列の逆行列を使うことで実現されるため、viewLoc に逆行列が渡されています。

このスクラップは2ヶ月前にクローズされました

ログインするとコメントできます

gl_Position = uProjectionMatrix * uViewMatrix * uModelMatrix * vec4(aPosition, 1.0); がなにをしているのかの図解

左目

右目

左目 (eye: "left")

右目

要するにこういうことらしい

おまけ：なぜビュー行列として view の変換行列の逆行列を渡している？

詳しい解説

まとめ

`gl_Position = uProjectionMatrix * uViewMatrix * uModelMatrix * vec4(aPosition, 1.0);` がなにをしているのかの図解

おまけ：なぜビュー行列として `view` の変換行列の逆行列を渡している？