Zenn
😽

論文読み: Fuzzy Edgeを用いた有向グラフを扱うGNNの性能改善に関する研究, ICLR2025

に公開
graph
neuralnetwork
GNN
wltest
iclr2025
idea

参考論文

Improving Graph Neural Networks by Learning Continuous Edge Directions
Seong Ho Pahng & Sahand Hormoz
ICLR2025

引用なしで画像を引いているような場合は本論文が出典です。
ところどころわかっていない部分もありますが、できる限りまとめました。
以下記事は、全て常体で書きます。

概要

  • 課題
    実世界グラフには有向性や流れの強弱といった連続的特徴があり、多くの GNN は無向・固定重みでしか扱えない。
  • 提案手法（CoED GNN）
    各エッジに連続値の位相角 θ を学習し、複素数値ラプラシアンで実部（outgoing）/虚部（incoming）を分離して情報を伝搬。
  • 理論貢献
    Fuzzy Graph Laplacian を用い、1–WL（弱形式 WL テスト）と同等の表現力を保持することを証明。
  • 実験成果
    • Synthetic Data（Triangular lattice/GRN）で他手法を大幅に上回る低 MSE
    • Real Data（Perturb-seq、Wikipedia web traffic、Power Grid）で一貫して最良性能

背景と目的

  • 従来 GNN の多くは無向かつ固定重みのメッセージパッシング方式
  • 実世界ネットワーク（交通、電力網、遺伝子調節など）では、一方向かつ強度の異なる情報流が重要
  • 既存の有向 GNN は離散的方向情報にとどまり、連続的流れを表現しにくい
  • 目的：連続的なエッジ方向性を学習可能にし、GNN の表現力・予測精度を向上させる

長距離の情報伝達が課題

提案手法：CoED GNN (Continuous Edge Directions GNN)

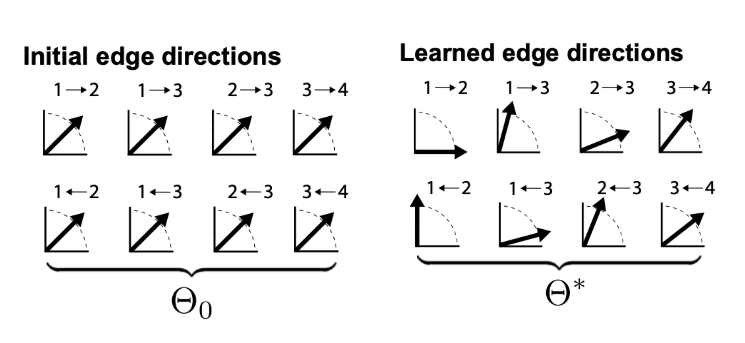
エッジ位相角 θ の学習

  • 各エッジ (i,j) に学習可能な位相角 θ₍ᵢⱼ₎ を割り当て
  • 複素ラプラシアンとして
    (L_{\mathrm{F}})_{ij}=\begin{cases}0,&\text{if }A_{ij}=A_{ji}=0,\\\exp\bigl(i\theta_{ij}\bigr),&\text{otherwise}.\end{cases}

    を定義し、実部で outgoing、虚部で incoming 集約を行う

メッセージパッシング

層 l の更新式：

F^{(l)}=\sigma\Bigl(F^{(l-1)}W_{\mathrm{self}}+m_{\leftarrow}^{(l)}W_{\leftarrow}+m_{\rightarrow}^{(l)}W_{\rightarrow}+B^{(l)}\Bigr)

  • 自己ループ項 + \theta学習付き双方向集約
  • これにより、有向かつ連続的な情報を統一的に処理できる
各項の説明
  • F^{(l)}:l層目のノードの特徴
  • W^{(l)}_{x}:l層目のノードの特徴を線形結合するための重み
  • F^{(l-1)}W^{(l)}_{self}:l-1層目のノードの特徴を線形結合して自身の情報を取り込む
  • m^{(l)}_{\leftarrow}W^{(l)}_{\leftarrow}:自身に流入するエッジからの情報を取り込む
  • m^{(l)}_{\rightarrow}W^{(l)}_{\rightarrow}:自身から流出するエッジから戻ってくるような、双方向性を考慮した情報を取り込む?
  • B^{(l)}:バイアス項
  • m_{\leftarrow} = P_{\leftarrow}F^{(l-1)}：入次数方向からの集約
  • m_{\rightarrow} = P_{\rightarrow}F^{(l-1)}：出次数方向からの集約
  • 伝播行列
    P_{\leftarrow}=D_{\leftarrow}^{-1/2}A_{\leftarrow}D_{\rightarrow}^{-1/2},\quad P_{\rightarrow}=D_{\rightarrow}^{-1/2}A_{\rightarrow}D_{\leftarrow}^{-1/2}

    により次数偏りを抑制
各項の説明
  • m^{(l)}_{x}:l層目の集約メッセージ
  • P_{x}:次数行列によって正規化を行なった行列(\leftarrow,\rightarrowの掛け算の順番はよくわかってない)
  • D_{x}:x方向の隣接行列の次数行列(対角行列)
  • A_{x}:入次数または出次数の隣接行列

理論的解析

CoED GNN は Fuzzy Graph Laplacian を用いることで、1–WL（弱形式 WL テスト）と同等のノード識別能力を持つことを証明

意義

従来有向グラフに用いられてきたMagnetic Laplacianは、同じく複素数であるが、Fuzzy Laplacianほどの表現力は持たなかった。(証明は同論文Appendix Fに記載)
原理的に、GNNは入次数と出次数を区別可能であるべきだが、隣接ノードの線型結合により、GNNはそのパラメータを全てのノードで共有してしまうという問題があった。
それゆえに、Magnetic Laplacianは、入次数と出次数を区別する能力を失い、結果的に表現力が低下していた。
一方で、本提案のLaplacianでは、実部と虚部を入次数と出次数のAggregationにそれぞれ独立に対応するため、そのような制約を受けない。

方向情報なしのノード分類実験

  • \thetaを固定し、Fuzzy LaplacianのIN/OUT集約の有効性を確認するための予備実験
  • 11種類の標準ノード分類ベンチマークに対して実験
    • 有向・無向グラフ
    • ホモフィリック・ヘテロフィリックグラフ
  • \thetaの設定値
    • 有向グラフ: 0 (incoming) / \pi (outgoing)
    • 無向グラフ: \pi/4

結果

少し見づらいが、ほぼ全てのベンチでTOP3に入っており、\thetaの情報がなくても一定程度はFuzzy Laplacianで方向情報を扱えることが確認できた。

Synthetic Data 実験

Triangular lattice

  • [-2,2]^2 上に二次ポテンシャル V を設定し、勾配からエッジ位相を割り当て
  • Input：ノルム1 正規化したランダム10次元ノード特徴 ×500インスタンス
  • Target：ポテンシャルVメッセージパッシングを10ステップ適用した後のノード表現

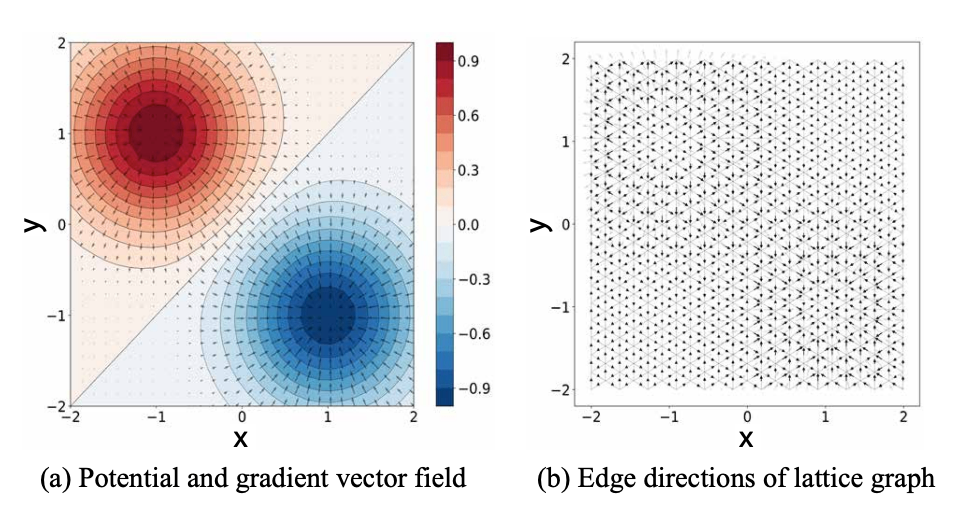
Gene Regulatory Network (GRN)

  • ノード200、有向エッジを ランダムで生成、活性化/抑制パラメータ付き
  • Input: 250ステップシミュレーションで取得した初期定常状態c
  • Target: ノックアウト摂動（対象ノードを0に）後さらに100ステップ後の定常状態c'

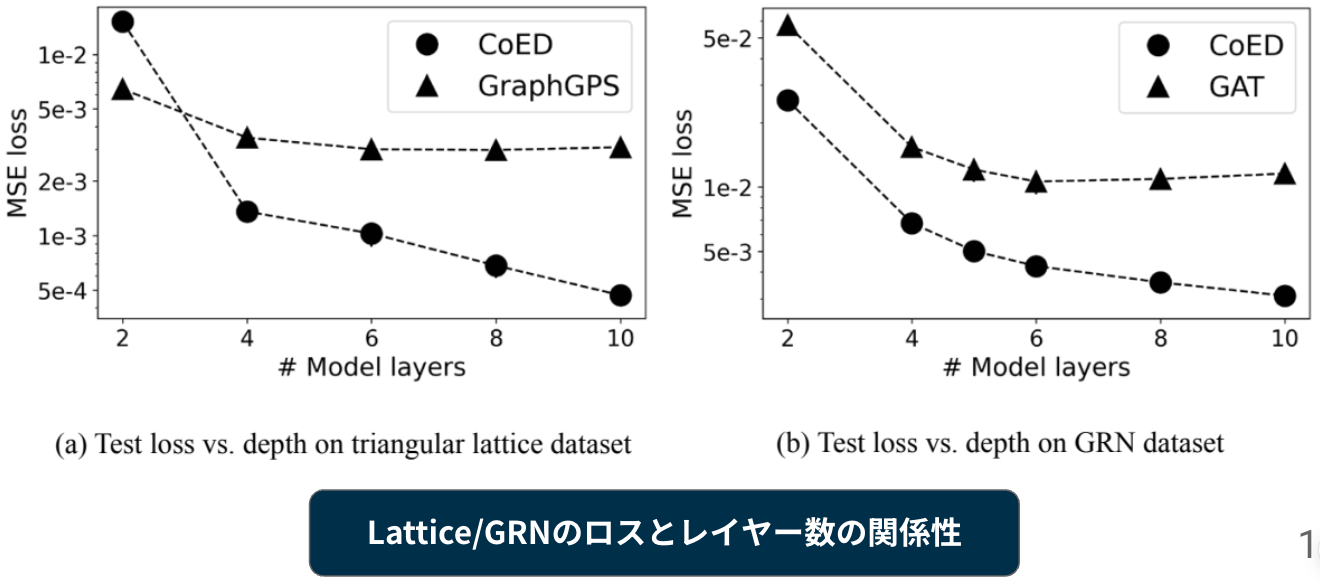
結果

  • 面倒だったので輪講用に作成したスライドをそのまま貼り付けた
  • Latticeにおいては、約2.6倍以上の性能向上
  • GRNにおいては、約2.4倍の性能向上

  • 4Layer以上で提案手法が優位性を示す結果が得られた

Real Data 実験

Single-cell Perturb-seq

  • データ：Replogle-gqps dataset
  • タスク：ノックアウト後の初期定常状態から、全遺伝子の発現レベルを予測
  • グラフ：発現相関に基づく k-NN（真の GRN 不明）
  • Input: ノックアウト後の初期定常状態
  • Target: 全遺伝子の発現レベル

Wikipedia Web Traffic

  • データ：WikiMath dataset (PyTorch Geometric Temporal Library)
  • グラフ：Wikipedia の有向リンク構造
  • タスク：当日のアクセス数から翌日を予測 (1step予測)
  • Input: 前日までのアクセス数
  • Target: 翌日のアクセス数
  • \thetaの意味: 記事同士の有向リンクの向き

Power Grid

  • データ: OPG (Optimal Power Flow) - Data (PyTorch Geometric Library)
  • グラフ: バスの繋がりを有向グラフで表現
    • バス: 発電機と負荷の接続点?

      In this dataset, a power grid is
      represented as a directed graph with nodes corresponding to buses (connection points for generators
      and loads) and edges representing transformers and AC lines., p10

    • エッジは、変圧器やAC線
  • タスク: 特定の負荷における電圧などの運用値から、発電機ノードのAC-OPF解の値を予測
  • Input: 特定の負荷における電圧などの運用値?

    Input features are the operating values
    of all components under specific load conditions, and the targets are the corresponding AC-OPF solution values at the generator nodes.

  • Target: 対応するAC-OPF解の値
  • \thetaの意味: バスのつながりの有向リンクの向き

結果

  • 全てのベンチマークにおいて、ベースラインを上回る結果を得られた

結論と今後の展望

  • 結論
    • CoED GNN は連続的エッジ方向を学習し、有向性を理論・実験の両面で有効活用
    • 表現力が弱形式の WL テストと同等の表現力を持つことを証明
    • Synthetic/Real いずれのデータでも一貫した性能向上を実証
  • 今後の課題
    • 各エッジについて\thetaを学習するため、大規模化した際にエッジ本数Eに比例して、メモリ使用量が増大する
    • \thetaの更新により、隣接行列が変化するため、Pの計算にオーバーヘッドが存在しており、Appendix G, TableG.2で、DirGNNに対して約2倍の計算時間を要することが報告されている
    • 本論文におけるGRNの実験と同様に、実データでは、ネットワーク構造が不明なことがあるためその場合において、\thetaの寄与とInterpretabilityについては別途考察が必要

Discussion