🧠
Brainf**k講座(番外編)「あしあと」問題解答コードの設計～実装

2024/12/01に公開
esolang
 はじめに※本記事は、2017/3/12にHatenaBlogに投稿した記事を移行したものです
久しぶりの講座ネタとして、最近締め切りを迎えた、CodeIQの「あしあと」を題材に、Brainf**kでのコードを設計し実装するまでを解説してみたいと思います。

※なお、Brainf**k講座本編に関しては、最後の第8回をご覧ください。
※CodeIQは既にサービス終了しているため、オリジナルのコンテンツは残っていません。Webアーカイブはこちらになります

 問題この問題は、次のような内容でした。
9×9のマス目の上を、入力に従って動く時、最終的な状態を出力する。
入力は、最後の改行以外は^v<>の4種類の文字からなり、それぞれ上下左右の1マス移動を表す。移動の順序は入力の順番そのまま。
開始地点は1行1マス目、とする。なお、移動によってマス目外に出ることは考慮しなくて良い。
マス目の状態の出力は、1行9文字、9行で行い、一度でも通ったマスはY、それ以外はxに置き換える。
例えば、>>>>>>>>vvvvvvvv<<<<<<<<^^^^^^^^という入力であれば、外周をぐるりと一周する動きを表しますから、出力は次のようになります。
YYYYYYYYY
YxxxxxxxY
YxxxxxxxY
YxxxxxxxY
YxxxxxxxY
YxxxxxxxY
YxxxxxxxY
YxxxxxxxY
YYYYYYYYY

 設計
 文字の判別さて、それではどのような実装にするかまずは設計を行うのですが、何を最初に気にするかというと、実は文字の判別だったりします。( 人によって違うとは思いますが )

Brainf**kでは,によって、1文字分の文字コードがセルに保存されます。もちろん、そこから判別すべき文字に対応する数値を引いてゼロ/非ゼロによって判別しても良いですが、流石にそこそこ大きな数を都度引くのには抵抗があります。そのため、大体は割り算を行って、出た余り ( 小さい数 ) によって場合分けを行うことを考えます。
さて今回は^v<>と改行、それぞれの文字コードは 94,118,60,62,10、実は余りでの判別という意味ではあまりよろしくありません。割る数を色々工夫しても、どうしても余りが被りがちだからです。なので、ここは商も活用します。幸い改行は文字コードが小さいので、商も必然的に小さくなります。今回5で割り算すれば改行以外は余りで判別できますから、大きな数の判断が不要になります。

すなわち、
商が2 → 改行
余り4 → 上
余り3 → 下
余り0 → 左
余り2 → 右

 セルの配置続いてセルの配置です。今回の問題は、入力を全部処理しないと、たとえ一部であっても出力内容が決まりません。そのため、9×9のマスの状態をセルに保持する必要があります。

そこでメジャーな言語だと、2次元配列に相当するものを使うことを考えられるところですが、Brainf**kにあるのは1次元のセルの並びだけです。なので、必然的に1次元配列化して考えます。ついでに、出力時の改行を処理しやすいように、行と行の間の区切り要素を設けておきます。これにより、行間移動は10要素の移動に置き換えることができます。
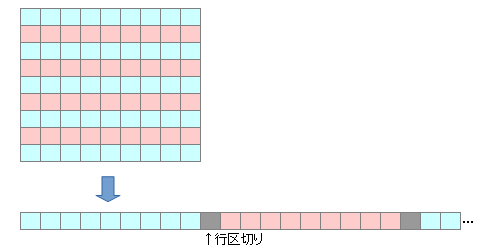
問題は、この配列の中でのポインタ移動です。このセル領域にいるところで文字入力、割り算、余りの判断とやるには、配列の間隔を5～6セル確保する必要があり、無駄に領域が広くなります。( そうしない方法もあるのですが… )

幸いにも、今回必要なのはあくまで要素間の相対移動 ( 上: -10要素、下: +10要素、左: -1要素、右: +1要素 ) なので、移動前の要素にマーク付けして一旦領域外に出て入力を処理し、マーク付けしたところまで戻って相対移動すれば十分です。
ということで、配列要素は最小限の2セル構成とします。最小限と言ってるのは、Brainf**kで配列を扱う場合、どうしても移動を管理するために1セルずつ空ける必要があるからです。
ともあれ、次の図のようにざっくりセルの配置が決まりました。なお、マスの移動を処理するときに端の存在は気にしなくて良いのですが、後で出力する時に終わりが分かった方が良いので、終端も設けます。

 処理の流れさてでは、処理の流れを考えます。大まかには、
領域のセットアップ ( 終端と改行の要素のデータ設定、初期位置の値設定とマーク付け )
入力処理～マス目移動～マスへの足跡付け ( 当該要素への値設定 )
出力処理
で、この中で肝となるのは、もちろん 2. の部分です。が、大体次のような流れにすれば、無理なく組むことができそうです。
Brainf**kの場合、距離を動的に計算しての移動は、実行時間的にも処理の複雑さ的にもなかなか厳しいのですが、決まった場所に移動するのは、マーク付けの管理を行えば十分です。

 実装では実際に実装を見ていきます。全体はすぐ下の折り畳み部分にあります。また、ideoneでの実行例はこちら です。これをベースに説明を加えていきます。
実装全体317B版
+++++[->++++++<]->[->++++++<]
>[-[->+<]>]
-<<+[++[-<++++++>]++<[-[-<+>]<]<+]
>>+<-<<<<<#
,+[
 -[>[->>>]<[>++++>+>]<<<-]
 >>--[[-]>-<<
  [-[-[->>
     >+[->+]>>
    <<]
    >>[
     >+[->+]>>>>>>>>>>>>>>>>>>>>
    ]
   <<]
   >>[
     >+[->+]<<<<<<<<<<<<<<<<<<<<
   ]
  ]>>[
     >+[->+]<<
  >>]
  <[-]+<-<+[-<+]<
 ]
<<,+]
>>>>>>+[
 <[+]>-[-[-
   <--<------->>
  ]
   <++<--->>
 ]
   <-<+++++++++++
 [->+++++++++++<]
 >.
>>>+]

 領域のセットアップ最初は領域のセットアップです。90要素180セルの終端を設ける必要がありますから、指定移動距離を使います。そして、配列にセットする値ですが、足跡は 1、行区切りは 2、未到達はそのまま 0 とし、マークは -1 としておきます。
   ** 仮終端をセットして、指定移動距離 **
 1: +++++[->++++++<]->[->++++++<]
 2: >[-[->+<]>]
   ** 終端をセットして、仮終端に戻るまで一定間隔で行区切りの値 ( 2 ) をセット
 3: -<<+[++[-<++++++>]++<[-[-<+>]<]<+]
   ** 初期位置のマークと足跡の値 ( 1 ) をセット
 4: >>+<-<<<<<
処理が終わった時のセルの状態は、次のようになっています。

 入力処理～マス目移動～マスへの足跡付けということで、いよいよメインの入力処理です。改行で処理は終わりなのですが、EOF検出の方が処理としては書き易いので、5行目～23行目のように、EOF(-1)検出のループを組みます。
 5: ,+[
…
23: <<,+]
で、文字を入力したら直ぐに割り算に移ります。が、ここではあくまで文字が判別できれば良いので、5で割った余りそのものが要るわけではありません。なので、スタンダードなアルゴリズムよりも1セル少なくて済むものを採用します。
 6:  -[>[->>>]<[>++++>+>]<<<-]
割る前に-1している ( 結果、,+と併せて素の文字コードを割り算する ) のは、改行コードに対する端数 ( 余りのような数 ) が丁度 0 になるからです。ともあれ、改行の時の商2以外で、マス目の分岐に入ります。
 7:  >>--[[-]>-<< ** 非改行で分岐、仮終端をセット **
…
22:  ]
さて、ここで4種の文字に応じて分岐があるわけですが、どこまで処理を共通化し、どこから分岐で処理を分けるか、を考えます。

処理の内訳としては、
現在の要素までマークを辿って移動
文字種に応じて相対移動
値とマークのセット
仮終端まで戻る
があるわけですが、1. の後に分岐するのは大変です。なぜなら、分岐のための条件が移動したその場にある必要があり、ということは割り算で出た端数を持ち運ぶことになるからです。

そのため、1. の前に分岐して、1.,2. をこなす所までは確定です。しかし、3.以降はまとめることができそうです。分岐を抜けた後に他の分岐に入らないように注意して次のように分岐します。
 8:   [-[-[->>
        * 端数3 →移動 *
 9:      >+[->+]>>
10:     <<]
11:     >>[
        * 端数2 ↓移動 *
12:      >+[->+]>>>>>>>>>>>>>>>>>>>>
13:     ]
14:    <<]
15:    >>[
        * 端数1 ↑移動 *
16:      >+[->+]<<<<<<<<<<<<<<<<<<<<
17:    ]
18:   ]>>[
        * 端数0 ←移動 *
19:      >+[->+]<<
20:   >>]
     * 値1、マークをセットして仮終端へ戻る *
21:   <[-]+<-<+[-<+]<
あくまで分岐で行うのは移動だけなので、すっきりと見易い構成になりました。

 出力処理入力処理を抜けたら、最後は出力のみです。終端が設定されているので、1セル置きに配置されている要素を辿っていくのみです。ただ、どこかにマークが残っていて邪魔になる可能性があるので、逐一クリアしていきます。
値としては、改行の2、Yの1、xの3種類です。これをそれぞれ、-1+11×1, 1+11×8, -1+11×11 と11をベースに構成します。if-else型で分岐を組むのはelseの制御が面倒になるので避け、当てはまった分岐以降の処理を全て通る形にしています。例えば、値2の改行であれば、(-2,-7),(+2,-3),(-1,+11) の全てを通り、合計(-1,1) の組を作り出します。
24: >>>>>>+[
25:  <[+]>-[-[-  * 残っているマークのクリアと分岐 *
      * 値2 改行 *
26:    <--<------->>
27:   ]
      * 値1 Y *
28:    <++<--->>
29:  ]
      * 値0 x *
30:    <-<+++++++++++
    * 11倍して加算 *
31:  [->+++++++++++<]
32:  >.
33: >>>+]
これで、実装が全て完了しました。

 終わりにいかがでしたでしょうか。実際にBrainf**kでコードを組む時の参考として、Brainf**k案件等実務に役立てて頂ければ幸いです。
また気が向いたら、ちょくちょく番外編を書くかも知れません。
はじめに

問題

設計

文字の判別

セルの配置

処理の流れ

実装

領域のセットアップ

入力処理～マス目移動～マスへの足跡付け

出力処理

終わりに

Discussion
