📝

C++で初等関数を扱う(構想編)

2024/08/08に公開

C++

プログラミング

関数

tech

はじめに

C++ですべての数学初等関数を扱うことのできるクラスを実装したので、本記事では実装経緯と、どのようにして実装したのかを書いていきます。同じようにクラスを実装する人の参考になれば幸いです。実際に作成したクラスとその使い方は別記事の方にあげているので、使いたい場合はそちらを参照してください。

別記事：実装したクラスとその使い方

初等関数とは

最初に今回扱う初等関数とは何かについて説明します。知っている方は飛ばして頂いて大丈夫です。
　一言でいえば「高校数学までで扱えるすべての関数」です。より正確にいえば、代数関数・指数関数・対数関数・三角関数・逆三角関数の有限回の合成により作ることのできる関数の総称です。代数関数との合成により加減乗除及び冪乗を行えるので、「多項式関数・指数関数・対数関数・三角関数・逆三角関数の加減乗除・冪乗・合成で作ることのできるすべての関数」とも表現できます。

実装経緯

理論計算を行ったり誤差計算を行ったりする際に数学関数を扱っており、そのほとんどは手計算やExcelで事足ります。しかしRunge-Kutta法などで多変数微分方程式を解いたり、誤差計算のために各変数で偏微分したりすると、手計算での計算ミスや、Excelでの書き間違いが多く発生するという問題が出てきました。そこでC++で簡単にあらゆる数学関数が扱えて、解析的微分もコンピュータに任せることができればミスを減らせると考え、あらゆる初等関数を扱えるクラス「SpFunc(Super Function)」を作成することにしました。

よって自作クラスSpFuncは次のことを作成目標としました。

すべての初等関数を表現することができること
多変数関数を扱えること
解析的偏微分ができること(数値微分のように極限をとって求めるのではなく、微分公式を用いて誤差なく導関数を求めること)
任意の関数の作成及び変数代入が簡単であること
原則として処理速度よりもコードの可読性を優先すること
数学に近い表記法を採用すること

関数の表現方法

まずは初等関数表現のための構成要素を考えました。「初等関数とは」の項で書いたように

定数
変数
数学関数(指数関数・対数関数・三角関数・逆三角関数)
加減乗除・冪乗演算(+ - * / ^)

を組み合わせればあらゆる初等関数を表すことができます。 ここで合成関数は片方の関数の1変数をもう片方の関数で置き換える操作なので、特別に要素として用意しなくても上4つの組み合わせによって表現することができます。指数関数も冪乗で表現可能ですが、私の分野的に $e^x$ が頻繁に登場すること、微分した際に $e^x$ は余計な係数がつかず扱いやすいことを理由に、数学関数exp()として構成要素の一つとしました。
　あとは4つの構成要素の組み合わせ順序を格納できれば、あらゆる初等関数を表現できます。そこで今回作ったSpFuncクラスでは括弧を用いず曖昧さを回避できる逆ポーランド記法を採用しました。 具体的にはstd::vectorをpublic継承しており、構成要素をその要素として逆ポーランド記法で格納します。ただし4つの構成要素が要素として格納されうるので、std::vectorは複数の型に対応できるstd::variantを要素とし、std::variantはdouble型(定数用)、及び3つのenum class(変数用・数学関数用・演算子用)を扱うことで任意の初等関数を表します。
　例としてこのクラスで $x^{1-0.5\sin{y}}$ を表現すると以下のようになります。

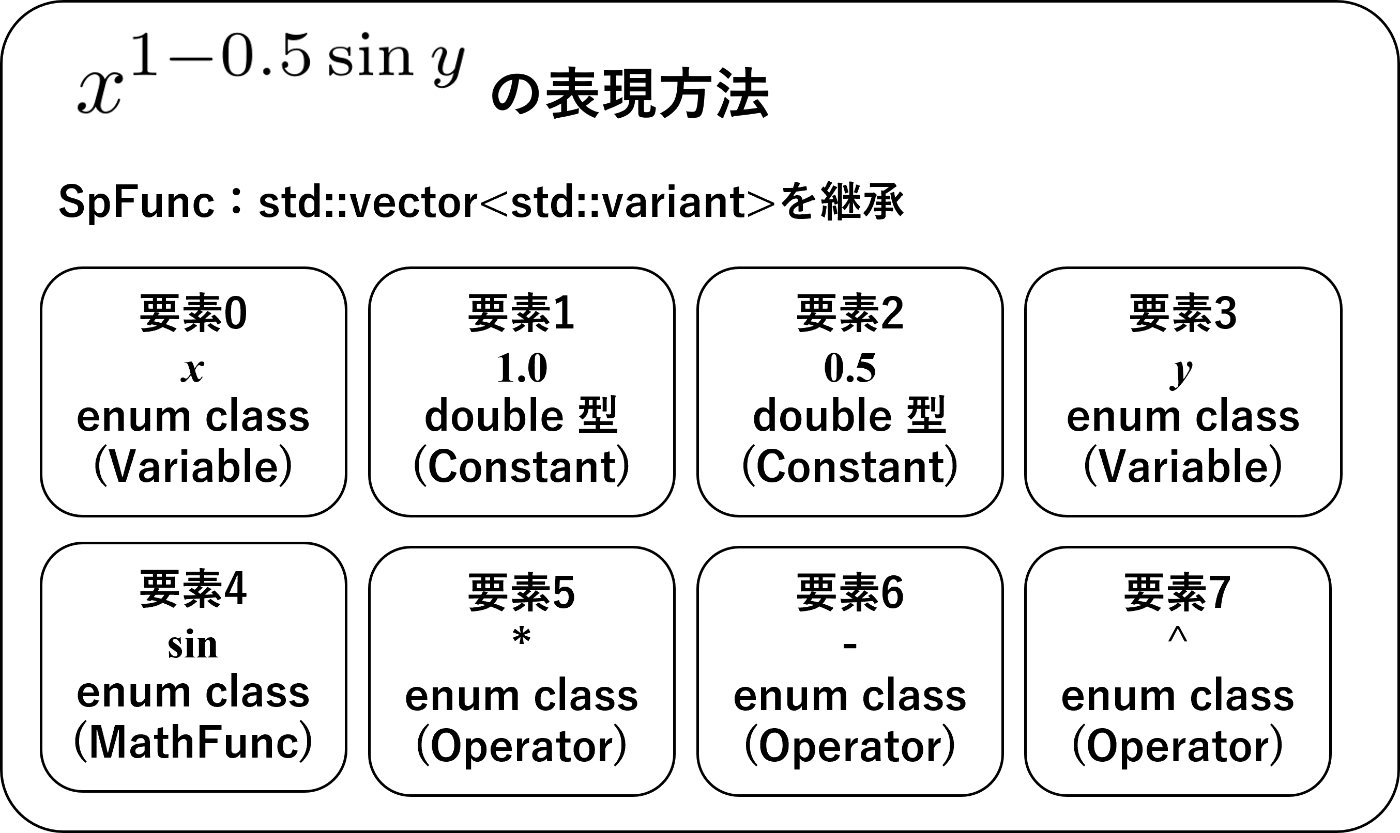
関数の表記法

前項で内部処理的な表現方法は決めましたが、我々は逆ポーランド記法を普段書かないため、中置記法で関数を入力したいわけです。数学関数に関してはstd::cmathと同様に exp(), log(), sin(), asin() のようにして中身となる関数を引数、結果を戻り値とすることで表現し、内部的にはその数学関数をシーケンスコンテナの最後に追加すれば表現できます。加減乗除・冪乗は当初はadd(),sub(),mult()と数学関数同様に関数を用意して入力することを考えましたが、数学関数よりも登場頻度がはるかに高いために非常に見づらくなるのが問題でした。そこで各演算子(+ - * / ^)をオーバーロードし、加減乗除・冪乗を扱えるように しました。この方法の利点は中置記法で加減乗除を簡潔に書けるだけではなく、特に指定しなくともコンパイラが乗除算の優先順位を上げて先に計算してくれるところにあります。ただし^はC++において排他的論理和を示すbit演算子で冪乗の意味はないのですが、LaTeX等に合わせて冪乗記号として採用しました。加えてoperator()をオーバーロードして変数への代入に対応させることで、できるだけ数学の表記に近い形で関数を扱えるように しました。

微分の実装

ここまでは初等関数をどのように入力し、内部で表現するのかという話でしたが、ここではそれらに対する演算処理をどのように実装するのかという話になります。初等関数の導関数は必ず初等関数になるので、SpFuncクラスに対する微分結果はSpFuncで格納できます。加えて和差積商の微分公式及び合成関数の微分公式、指数関数・対数関数・三角関数・逆三角関数の微分公式がすべて存在しており、初等関数はこれらの組み合わせなので、これらの公式を有限回用いればあらゆる初等関数は微分できます。そこで微分処理を行う関数を再帰関数として微分公式を適用し解きます。
　前項のような逆ポーランド記法で関数を表記する場合、すべての関数のシーケンスコンテナは次の4ついずれかの形になります。

<定数>1つのみ
<変数>1つのみ
(関数A) + <数学関数F>
(関数A) + (関数B) + <加減乗除・冪乗演算子G>

この分類の嬉しいところは、これらはシーケンスコンテナの最後の要素の種類がそれぞれ違うため、そこだけ見れば判定可能なことです。 これらそれぞれに対する微分を考えると、1つ目は常に0、2つ目は微分する変数とされる変数が一致していれば1,そうでなければ0となります。3つ目は末尾の数学関数Fと関数Aの合成関数であるので、関数A及びその導関数・数学関数Fの導関数・合成関数の微分公式で表せます。4つ目は末尾の演算子Gに対する微分公式を用いればよいので、関数A及びその導関数・関数B及びその導関数・演算子Gに対する微分公式で表すことができます。以上のことから (関数A),(関数B)部分の導関数を求めるために微分を再度呼び出せば、あとは末尾の要素の種類で場合分けを行うことであらゆる初等関数の導関数が計算できます。
　ただし変数や定数を微分するたびに導関数として1や0が大量に出てくる関係上、微分を行った際に×1や×0などがついた項が大量に出てきてしまうので、特に対策せず実装すると導関数の要素数が無駄に多くなり、処理速度も低下してしまいます。こういった定数倍程度なら場合分けも簡単ですが、例えば同じ関数の積を2乗で置き換えたり、 $\frac{x}{x}$ を1に置き換えたりといった対応もすると、操作は非常に複雑になります。今回は処理速度よりも可読性を優先するため、要素数削減のための対応は最小限としました。

おわりに

この記事では数学関数全般をプログラミング言語上で簡単に扱えるようにすることを目指して作った自作クラスSpFuncについて、欲しいと思った機能とその実装方法を書きました。クラスを実装する上で一番大事だと感じたのは、目的とする機能と優先するべき性能を明確にしてから作成し始めることです。 欲しい機能を実装する方法は基本的に複数ありますが、どれも一長一短であり、それらのうちどれを採用するべきかは他の機能や求める性能によって変わります。実装方法によっては他の機能の実装をやりづらくしたり、必要以上の性能追及のせいでコードを複雑にしたりしてしまいます。そのため実装方法を考える前に、何が必要で何を優先するのかをできるだけ詳細に決定しておくことが、良い実装を行うための一番の近道となると思います。

廃案

クラスSpFuncでは最終的に関数の表記法として逆ポーランド記法を採用していますが、クラスの実装当初は異なる実装方法を採用していました。供養と何らかの参考になればと思いここに書いておきます。
　その実装方法ではクラスにenum class型,SpFunc*型、void*型の3つをメンバ変数として持たせて表現します。enum class型で何が格納されているのかを表し、他2つのポインタ型で他のSpFuncのインスタンスや定数の値などに繋げます。この方法で $x^{1-0.5\sin{y}}$ を表現すると以下のようになります。

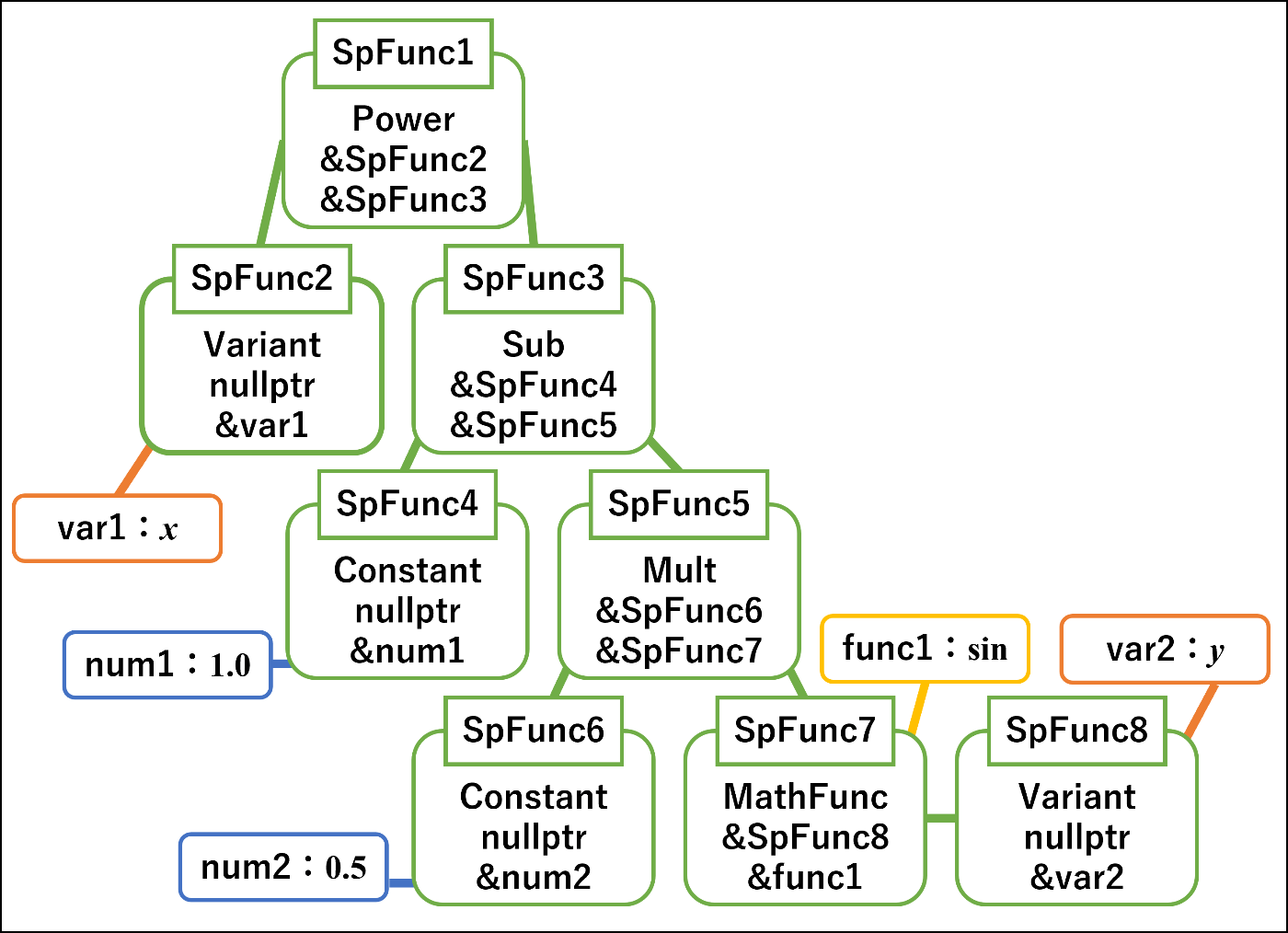
逆ポーランド記法と比較したときのこの方法の利点は、std::variantを使わないのでC++14以前でも使えることと、関数を再利用するときにはポインタを付け替えるだけなので定数時間で済むことです。しかし1つの関数につき大量のインスタンスとポインタが必要になるのでメモリ管理が面倒であり、バグが多く発生したため廃案となりました。ただし微分はこちらで実装した方が高速であったため、速度を求める実装では使える可能性があります。

参考文献

[1] 初等関数 Wikipedia

[2] 逆ポーランド記法 Wikipedia