1982 SAT math Q17 (coin rotation paradox)

イギリスの共通テストの過去問で選択肢に正解がなかった, という話.

先人の素晴らしい説明はこちら(ただし, 9:18-9:45, 10:22くらいのアニメーションには不適切な部分がある), wikipeida はこちら.

以下の記事にある Animation GIF の作り方はこちら.

1. 問題と解答

1.1 出題された問題

17. In the figure above, the radius of circle A is 1/3 the radius of circle B. Starting from the position shown in the figure, circle A rolls around circle B. At the end of how many revolutions of circle A will the center of circle first reach its starting point?
    　
    (A) $\dfrac{3}{2}$　　(B) 3　　(C) 6　　(D) $\dfrac{9}{2}$　　(E) 9

(円Aの半径は円Bの半径の1/3. 円Aが図の位置から円Bのまわりをまわるとき, 最初の位置に戻るまでに円Aは何回回転するか?)

1.2 ナイーブな答え

円Aの半径を $r$ とすると, 円Bの半径は $3r$. このとき, 円Aの円周は $2\pi r$, 円Bの円周は $2\pi \cdot 3r = 6\pi r$. これより, $\dfrac{6\pi r}{2\pi r}=3$. 答えは選択肢 (B).

(要するに, 半径が3倍なら円周も3倍. したがって3回転.)

1.3 正しい(と思われる)回答

ところが, 実際に問題文に従い円Aを円Bの周りに回転させてみると, 以下のようになる.

4回転している! これだと正解が選択肢にない, ということで大騒ぎになったらしい. 4回転になる理由は円Bの円周の長さを転がることによる3回転と, 円Aが円Bを公転しながら1回転していることによる. 詳細については以下の記述を参照.

1.4 ナイーブな答え再び

しかし, 「円周が3倍だから3回転」というのはまったく間違いなのかというとそうでもない. 円Aの後ろにくっついて観察している人(自分が円Bに沿って移動していることに気付いておらず, 直線的に移動していると思っている人)の視点考えると, 円Aが一回転したように見えるのは図のアルファベットAが円Bの円周に対して平行に横たわった状態になったときなので, 円Aの回転の数え方は以下のようになる.

3回転! したがって, 選択肢(B)も間違いとはいえないであろう.

1.5 問題の所在

結局何が問題だったかというと, 問題文にあった "revolutions of circle A" が何を意味するかがあいまいだった, ということ. 全体を俯瞰した視点(試験の回答者の視点, グローバル座標)で見れば4回転だし, 円Aに寄り添った視点(ローカル座標)で見れば3回転, ということになる. さらに "revolution" には「公転」という意味もあるので、その場合は1回転が正解となる. なので, 問題文にそれを特定できる文言を入れておくべきだった, ということになる.

(最終的に試験としてはこの問題については採点対象にしない, という取り扱いになったようだ.)

2. 回転数の公式

グローバル座標で見ると4回転になる, というのを数学的に導出しよう.

2.1 命題

最初に以下の命題を示す.

命題: 円Aの回転量は円Aの中心の移動距離に等しい(最初にリンクを示した動画の中では "The amount the small circle rotates = the distance its center travels" と述べられている).

説明: 円Aが円Bの周囲を回転するとき, 円Aの中心の速度を $V$ とする. 円Aは滑らずに円Bの円周上を転がるので, 円Aと円Bが接している点の瞬間的な速度は0(円Aが転がるとき円Bと接していた点は後ろに置き去りにされる). これを円Aの中心が静止している座標系で観測すると, 両者は逆の関係になり, 円Aの中心の速度は0で円Aの円周の速度が $-V$ となる(※). 両者の速度の大きさは同じ(向きは異なる)であるから, 最終的な移動距離も同じになる. $\Box$

(※についての深堀りは後続の3.節を参照のこと.)

この命題を適用してみよう. 円Aの中心の軌跡は半径 $4r$ の円なので, その長さは $2\pi (4r)=8\pi r$.

したがって円Aは $8\pi r / 2\pi r = 4$ 回転する.

2.2 他の例

一般に円Aがどのような図形を転がったとしても, 以下の公式から(グローバル座標系における)回転数を求めることができる(外周が交わってるとかギザギザの図形など転がれない図形は除く). 図形の周の長さを $L$ とすると, 円Aが図形の外側を回転する場合, 円Aの中心の軌跡の長さは $L+2\pi r$ となり, 回転数 $n$ は,

$$n = \dfrac{L+2\pi r}{2\pi r} = N + 1$$

となる. 一方円Aが図形の内側を回転する場合, 円Aの中心の軌跡の長さは $L-2\pi r$ となり, 回転数 $n$ は,

$$n = \dfrac{L-2\pi r}{2\pi r} = N - 1$$

となる.

2.2.1 (例)円の内側を転がる場合

円Aが円Bの内側を転がる場合を考える.

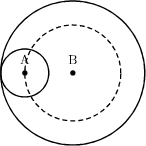
円Aの中心は半径 $2r$ の円周上を移動するので, 回転数 $n$ は以下のように計算できる.

$$n = \dfrac{2\pi \cdot 2r}{2\pi r} = 2$$

2.2.2 (例)三角形の外側を転がる場合

転がる対象は円でなくてもよい. 一辺が $2\pi r$ の正三角形Cの周りを転がる場合を考える.

円Aの中心は, 正三角形Cの各辺上では各辺に平行に移動するとともに, 頂点では120度ずつ回転し, 3つの頂点合計でちょうど1回転分移動する. したがって回転数 $n$ は以下のように計算できる.

$$n = \dfrac{3\cdot 2\pi r + 2\pi r}{2\pi r} = 4$$

3. 命題に関する疑問

前節で見た命題について, 円Aの中心が静止している座標系では円Aの円周の速度が $-V$ であることを見た. これはまぁそうかなと思えるのだが, 一方で, 以下のような疑問も感じた.

「円Aの円周のうち, 円Bとの接点を考えるとは円B上の点でもあるのだから, その移動距離は $2\pi \cdot 3r$ にしかならないのでは? また, 円Bを円Aの周りに転がした場合と何が違うのか?」

このような疑問を解決するため, もう少し調べてみよう.

3.1 円Bが円Aの周りを回る場合との比較

まず, 比較のため, 円Aの中心が静止する座標系への変換の1つである, 円Bが円Aの周りを回る場合を考えよう.

円Aと円Bの接点は単純に円Bの円周上を移動するだけなので, $6\pi r$ しか移動せず, 命題の説明には合わない(最初に挙げた参考動画ではこのアニメーションに似た画像がイメージ画像として使われているが, 何かの間違いだと思われる).

次に, 円Aが円Bの周りを回る場合を円Aの中心(のみ)が静止している座標系(円A自身の回転はそのままの座標系)で見ると以下のとおり.

円Aの中心は静止しているが, 円Aの円周は回転しており, 命題の説明に合ったイメージになる. 円Aと円Bの接点よりも円Aの円周の方が速く動いている点に注意. 円Aと円Bの接点は $6\pi r$ しか移動しないが, 円Aの円周はそれよりも早く動いているので, もっと多く移動している. 実際数えてみると確かに4回転($8\pi r$分)している(ちなみに, 円Aの中心だけでなく, 回転まで静止する座標系に変換すると, 上のアニメーション(円Bが円Aの周りを回る場合)と一致する).

元のアニメーションとこのアニメーションを比較することにより, 命題の主張である「円Aの中心の軌跡の長さと円Aの円周の移動する距離が等しい」ということが視覚的に理解できる.

3.2 角速度を使った解の導出

命題の方向性に合わせ物理学っぽい計算イメージでこの問題を解いてみよう.

グローバル座標系における円Aの中心の速度を $V$[m/s] とする. 上で見たように円Aの中心が静止した座標系で見ると円Aの円周は速度 $-V$ であるから, 回転の角速度は $\omega = V/r$[rad/s] となる.

円Aの中心は $2\pi (r+R)$[m] 移動するので, 移動にかかる時間は $t = \dfrac{2\pi (r+R)}{V}$[s]. したがって, 円Aの回転角は $\theta = \omega t = \dfrac{V}{r} \dfrac{2\pi (r+R)}{V} = \dfrac{2\pi (r+R)}{r}$[rad]. したがって回転数は $n = \theta / 2\pi = 1 + \dfrac{R}{r}$[回].

$R=3r$ であれば答えは $n=4$ 回となり, 正しい答えが得られる.

4. ダイレクトな解法

ここまで基本的には上で挙げた動画に沿って説明してきたが, もう少しダイレクトに説明することもできる.

実は今回の記事の中にあるアニメーションを作成するときに, ここで紹介する考え方を使っている. 概要は以下のとおり.

• 円Aが円Bの周りを10度回転するごとに1コマとする
• 円Aの中心が円Bの中心に対して $\theta$ 回転したときのコマは以下の手順で作成する
  • 円Aの中心を原点におく
    
  • 円Aを時計回りに $3\theta$ 回転させる
    
  • 円Aを初期位置まで平行移動
    
  • 円Bの中心に対して時計回りに$\theta$ 回転させる
    
    このとき, $\theta$ を図示すると以下のようになる
    
• これを0度から360度まで10度ごとに繰り返しすべてのコマを出力する

この手順からわかるように, 3回転分は円Bの円周の長さ分を転がることにより発生し, 1回転分は円Aが円Bの周りを公転することにより発生している.

実際に MetaPost のコード全体を示すと以下のようになる.

fig.mp

% アウトプットファイルフォーマットの指定
prologues := 3;
outputtemplate := "%j/%6c.%o";
outputformat := "png";

u=1in;

% bounding box 用のパス(実際の設定は最後)
path bb;
bb = (-1.5u,-1.5u)--(1.5u,-1.5u)--(1.5u,1.5u)--(-1.5u,1.5u)--cycle;

% 円A, 円B を準備
picture a,b;
a := image(
  pickup pencircle scaled 4pt;
  drawdot (0,0);
  pickup pencircle scaled 1pt;
  draw fullcircle scaled 0.5u;
  label.top(btex A etex,(0,0.05u));
  pickup defaultpen;
);
b := image(
  pickup pencircle scaled 4pt;
  drawdot (0,0);
  pickup pencircle scaled 1pt;
  draw fullcircle scaled 1.5u;
  label.top(btex B etex,(0,0.05u));
  pickup defaultpen;
);

% 円Bの中心に対して10度ずつでコマ割り
for i=0 upto 360:

% iコマ目の描画
beginfig(i);

  picture pic;
  pic := image(
    % 円Aを回転させ正しい位置に配置
    draw a rotated (-3i) shifted (-u,0) rotated -i;
    draw b;
  );

  % 全体を一気に描画
  draw pic;
  % 円Aの中心が静止した座標系で描画する場合の記述
  % draw pic shifted (u*cosd(i),-u*sind(i));

  % bounding box の指定(全コマ同じ大きさの画像にする必要がある)
  setbounds currentpicture to bb;

  % Windows 用のDPI調整
  currentpicture := currentpicture scaled (96/72);
endfig;

endfor

end

コード内のコメントにも記載しているが, 上に挙げた手順を実施しているのが以下の部分.

  draw a rotated (-3i) shifted (-u,0) rotated -i;

円Bの中心にある円Aを時計回りに3i回転し, 初期位置に平行移動, そこから円Bの中心に対して時計回りにi回転させる, という命令になっている.

また, 円Aの中心が静止した座標系のアニメーションを作成するためには上のコードの

  draw pic;

を

  draw pic shifted (u*cosd(i),-u*sind(i));

とすればよい. これは円A, 円Bが含まれた画像全体を円Aの中心が原点(円Bの中心があった場所)になるように平行移動することを表している. ここで, cosd, sind は度(degree)を引数とする三角関数(通常の三角関数はラジアンを引数とする)である.

参考までに png ファイルをアニメーション gif に変換する julia プログラム(REPLにコピペする)

fig.jl

import Printf.@sprintf
import Plots:Animation, buildanimation  

nframes =360
fnames = [@sprintf("%06d.png", k) for k  in 0:nframes]   
anim = Animation("fig", fnames); #fig is the folder name which contains the pngs
buildanimation(anim, "fig.gif", fps = 12, show_msg=false)

実際に作成されるアニメーション:

5. まとめ

記事を書く中で, 参考動画を見ただけではきちんと理解できていなかった部分(特に命題の主張の部分)が自分でアニメーションを作成してみることによりよく理解できた.

MetaPost ならこれくらいのアニメーションは数学的に正確なものがパパっと作れるのは便利だと思った(マウスで図形の位置とか大きさとか角度とか調整して,,, とかするのは想像しただけで悪夢に思える).