勾配ベクトル(gradient)について

勾配ベクトルの方向は関数が最も大きく増加する方向, というのをいろいろ考えてみた. (用語の使い方とかベクトルの表示の仕方とか適当なのはご容赦ください.) ...と考えてみたけど自分の理解の整理になっただけで特にこれといってめぼしいことはない, かな(笑).

0. 動機

勾配(gradient)ベクトルは関数が最も大きく増加する方向, というのは有名な話で, ネットをみればいくらでも説明・証明しているサイトが見つかる. 証明は数学的には簡単だが, 勾配ベクトルの式を見ても「関数が最も大きく増加する方向」かどうかは(自分には)いまいちピンとこない. そこで, 勾配ベクトルが本当に「関数が最も大きく増加する方向」になっているかどうかについてあれこれ考えてみた.

1. 勾配ベクトルの意味

勾配ベクトルの方向が, 関数が最も大きく増加する方向であることのよくある証明について簡単に振り返る.

関数 $f(x,y)$ の変化は以下のように計算できる.

$$\begin{align*} \Delta f &= f(x+\Delta x,y+\Delta y)-f(x,y) \\ &\sim \dfrac{\partial f}{\partial x}\Delta x + \dfrac{\partial f}{\partial y}\Delta y \\ &= \vec\nabla f \cdot \Delta \vec x \\ &= |\vec\nabla f| |\Delta \vec x| \cos \theta \end{align*}$$

ここで $\theta$ は $\vec\nabla f$ と $\Delta x$ のなす角. $\Delta f$ を最大にするためにには $\theta=0$ であればよい. すなわち $\Delta \vec x$ が $\vec\nabla f$ の方向を向いているときに関数の変化が最大になる. このことから勾配ベクトル $\vec \nabla f$ の方向は関数が最も大きく増加する方向であるといえる.

2. 疑問

前節の結論は, 勾配ベクトル $\vec\nabla f$ の方向が, 関数 $f$ が最も大きく増加する方向, ということであるが, 勾配ベクトルを眺めてみてもそのようなイメージがわかずモヤモヤする.

$$\vec\nabla f = \Big( \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y} \Big)$$(しないかな?)

3. 単純化

微小変化を考えれば, 曲率などは無視できる. そこで1次の効果のみに注目して, 関数 $f$ に対する接平面$\tilde{f}$を考える.

$$\begin{align*} \tilde{f}&=ax+by+c , \quad a=\dfrac{\partial f}{\partial x} , \quad b=\dfrac{\partial f}{\partial y} \\ \Delta \tilde{f} &= a \Delta x + b \Delta y \end{align*}$$

この式は $x$ 方向(例えば東)に1進むと$a$上昇し, $y$ 方向(例えば北)に1進むと$b$上昇することを意味している. このとき, $f$ が最も大きく増加する方向はどっちだろうか? 例えば, $a=b=1$ のとき,

$$\tilde{f}=x+y+c$$

$x$ 方向(東)だけ, $y$ 方向(北)だけに1進むとそれぞれ1しか上昇しないが, 直観的に $x$ 方向と $y$ 方向の中間方向(北東)に進むとよさそうなことがわかる. 実際, 中間方向(北東)に1進むと, $\Delta x = \Delta y = \sqrt{2}/2$ なので, $\Delta \tilde{f} = \sqrt{2}(=1.4142\cdots)$ 上昇することができる.

直観的ではなく合理的に説明することは可能だろうか. もちろん最初に示した証明のように計算することはできるがもう少しピンとくる説明はないものか.

4. 法線ベクトルを考える

接平面の方程式を以下のように書き換える.

$$\begin{align*} -ax-by+\tilde{f}&=c\\ \vec{n}\cdot \vec{x}&=c\\ \end{align*}$$

法線ベクトルは $\vec{n}=(-a,-b,1)$ なので, 最も大きく減少する方向は法線ベクトルの $x$, $y$ 成分の方向, つまり $(-a,-b)$. 接平面上で, 最も大きく増加する方向はその反対側なので, $(a,b)$の方向. これは勾配ベクトルの方向である.

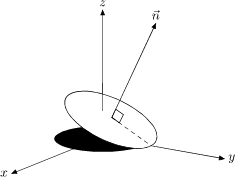
図のプログラムコード(FeatPost)

fig.mp

prologues := 3;
outputtemplate := "%j/%3c.%o";
outputformat := "svg";
% outputformat := "png";

input featpost3Dplus2D;

beginfig(1);

% basic parameters
f:=(3,2,1);
Spread:=72;

% axis
drawarrow rp((0,0,0))--rp((1.25,0,0));
label.lft(btex $x$ etex,rp((1.25,0,0)));
drawarrow rp((0,0,0))--rp((0,1.25,0));
label.rt(btex $y$ etex,rp((0,1.25,0)));
drawarrow rp((0,0,0))--rp((0,0,1.25));
label.top(btex $z$ etex,rp((0,0,1.25)));

% disc, shadow, center (= normal vector)
% 影の描画は適当(rigorouscircle は影の描画対象ではないため)
numeric radius;
path dsc,shdw;
color cntr;

cntr=(0,1/sqrt(5),2/sqrt(5))/4;
radius=0.5;
dsc=rigorouscircle(cntr,cntr,radius);
shdw=rigorouscircle(black,blue,radius);

% 図形の描画
fill shdw; 
fill dsc withcolor white;
draw dsc;
draw rp(cntr)--rp((0,sqrt(5),0)/4) dashed evenly;

% 法線ベクトル
drawarrow rp(cntr)--rp(5*cntr);
% 直角マーク
squareangline(5*cntr,(0,sqrt(5),0)/4,cntr,0.1);
% z軸の下の方を書き直し(終点は適当)
draw rp((0,0,sqrt(5)/2)/4)--rp((0,0,sqrt(5))/4);

% windows向けDPI調整
currentpicture := currentpicture scaled (96/72);
endfig;

FeatPost は MetaPost 用の3次元ライブラリ. FeatPost については別記事で説明予定.

これはなかなか直観的だが勾配ベクトル, 接平面, 法線ベクトル, その逆方向, と少し遠回りな気もする.

5. 成分表示での確認

接平面における $\Delta\tilde{f}$ の式に戻って,

$$\Delta \tilde{f} = a \Delta x + b \Delta y$$

ここで, $xy$平面で $\varphi$ の方向に1だけ移動する場合を想定して, $\Delta x=\cos \varphi$, $\Delta y=\sin \varphi$ とおいて変形すると,

$$\begin{align*} \Delta \tilde{f} &= a \cos\varphi + b \sin\varphi \\ &=\sqrt{a^2+b^2}\Big(\dfrac{a}{\sqrt{a^2+b^2}}\cos\varphi+\dfrac{b}{\sqrt{a^2+b^2}}\sin\varphi\Big) \\ &=\sqrt{a^2+b^2}(\cos\alpha\cos\varphi+\sin\alpha\sin\varphi) \\ &=\sqrt{a^2+b^2}\cos(\alpha-\varphi) \end{align*}$$

ここで, $\alpha$は$(a,b)$の方向, すなわち勾配ベクトルの方向である. これが最大になるためには $\varphi=\alpha$, すなわち, 勾配ベクトルの方向に移動すればよい($\theta=\alpha-\varphi$ であり, 結局最初の証明を成分表示でなぞっただけ).

6. まとめ

最初に変化率である勾配ベクトルを方向ベクトルのように扱うところがモヤモヤする, と書いたが, これは勾配ベクトル自体が問題ではなく, 結局, そんな風に思う自分に問題があるのかもしれない.

上の証明や考察では勾配ベクトル自体を方向ベクトルとして扱っているわけではなく, 勾配ベクトルは変化率のリストとして扱い, それを最も有効活用できる方向を求める, という方向で議論している. その結果, 勾配ベクトルの方向に変化した場合に最も効率よく勾配ベクトルを利用でき, 変化が最大になる.

したがって,

勾配ベクトルは関数の変化が最大になる方向

というのを頭の中で

勾配ベクトルの成分の値と同じ比率で移動方向を決定すれば関数の変化を最大化できる

という感じで解釈すれば, 勾配ベクトルはあくまで移動方向を決めるための材料として使っていて, 方向ベクトルとして使っているわけではないからモヤモヤしないかも!

でも, 少し落ち着いて読み返してみると, どちらでも大して違いはない気もしてきた. 結局のところもともとの表現である「勾配ベクトルは関数の変化が最大になる方向」っていうのが簡潔でいいんじゃないかと思えてきた...(涙)