錐の体積が柱の体積の 1/次元 であること

$N$次元錐の体積が$N$次元柱の体積の$1/N$であることを適当に理解する. ちまたに同じテーマを扱ったページは大量にあるが, $N$次元を対称に取り扱かおうとしているところが特徴的かもしれない.

1. イントロダクション

以前にも紹介した測度の考え方 という本の 1.5 錐体の体積はなぜ柱体の1/3か, という節のところで,

三角形の面積(2次元):

$$U_2 = \dfrac{1}{2}xy = \dfrac{1}{2} V_2$$

三角錐の体積(3次元):

$$U_3 = \dfrac{1}{3}xyz = \dfrac{1}{3} V_3$$

これには関係があるはずだ, というような記載があったが, 残念ながらこの文脈での深堀はされていなかった. 具体的にはこれらから類推すると, $N$次元錐の体積は, 以下のように予想されるはず.

$$U_N = \dfrac{1}{N}x_1 \cdots x_N = \dfrac{1}{N} V_N$$

これをこの文脈で(対称性を保って)説明してほしかったのだが, 残念ながら続く記載は積分の考え方による説明(錐の頂点方向を特別扱いした説明, 以下に続く節参照)になってしまい, ちょっと肩透かしな感じだった(本自体は大変すばらしい本なので, 特に大学時代にルベーグ積分をちゃんと学ぶ機会がなかった人には超オススメ).

2. 積分を使った説明

次元を対称に扱う方法の前に積分を使った説明について見ておこう. $N$次元錐は底面を$N-1$次元超平面とし, $N$次元目の頂点までを高さとする立体とし, 底面である $N-1$次元超平面の「面積」を $S$ とする.

図のように超平面を底面とし「高さ」が $x$ であるような$N$次元錐を考える. $0\le t\le x$ であるような $t$ における断面を考えると, その面積は各軸方向に $t/x$ の比率で縮小されているから,

$$\Big(\dfrac{t}{x}\Big)^{N-1} S_{N-1}$$

錐の体積はこれを $0\le t\le x$ で積分すればよいから,

$$\begin{align*} U_N &= \int_0^x \Big(\dfrac{t}{x}\Big)^{N-1} S_{N-1} dt \\ &= \dfrac{1}{N}xS_{N-1} \\ &= \dfrac{1}{N} V_N \end{align*}$$

3. 対称性を保った説明

前節の説明で何も問題はないのだが, 積分で説明しようとすると特定の軸だけ特別扱いしている点がちょっと不満. またそのせいで $1/N$ の $N$ が次元の数というのがあまり明確でない気がする. 何とか対称性を保ったままで説明できないだろうか? と思ってひねり出したのが以下の説明.

以下のような $N$次元柱の中心で向き合う2つの錐を考える.

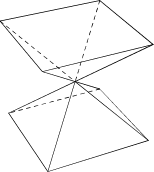
ここで, 錐の体積が柱の体積に比例することは所与であるとし, その比例係数を $a$ としよう. すると上図の個々の錐は元の柱の半分の柱に対する錐だからその体積は,

$$a\cdot\Big(\dfrac{V_N}{2}\Big)$$

2つ合わせると

$$a\cdot V_N$$

これは比例係数の定義から元の $V_N$ に対する錐, すなわち $N$次元柱に対する $N$次元錐の体積を表している.

$$U_N = a\cdot V_N$$

$a$ を求めるには, このような錐のペアが空間の軸の数だけ($N$次元ならば$N$個)存在し, それらをすべて組み合わせると元の柱が再現されることに注意する. すなわち,

$$N\cdot a\cdot V_N = V_N$$

これを $a$ について解くと

$$a = \dfrac{1}{N}$$

したがって,

$$U_N = \dfrac{1}{N} V_N$$

個人的には対称性を保ったままそこそこ納得感のある説明に思える. まあ、証明するとは言ってないということで温かい目で見守っていただけるとうれしいです(笑).