Zenn
👻

Hello, FeatPost!

2025/03/14に公開
metapost
featpost
tech

MetaPost の3Dパッケージである FeatPost を試してみた.

0. FeatPostとは?

FeatPost は MetaPost の3Dライブラリである. リリースノート を見ると, ver 0.8.8 (2012/04/16) が最終リリースになるとのこと.

他にもいくつか MetaPost で使用できる3Dライブラリはありそう(こちらなど)だが, 一番お手軽な感じがしたので FeatPost を試してみることにした.

参考文献:

  1. FeatPost manual
  2. FeatPost and a Review of 3D MetaPost Packages
  3. FeatPost macros

(FeatPost macros は FeatPost manual の昔のバージョンかもしれないが, 参考にはなる.)

1. Hello, FeatPost!

最初に, いわゆる "Hello, World!" 的なプログラムを考える.

input featpost;

beginfig(i);
cartaxes(1,1,1);

% DPI adj. for windows
currentpicture := currentpicture scaled (96/72);
endfig;

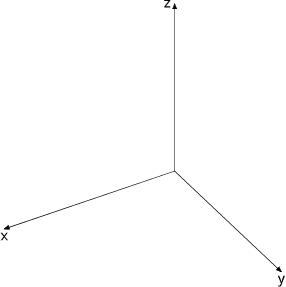
x, y, z 軸が表示されるだけの単純なもの. これを見ると以下のような点に気付く.

  • cartaxesの引数は各軸の長さを表すが, 全部1になっている. MetaPost でただの1は 1pt を表すが, アウトプットを見るともっと大きく見える.
  • 座標軸のラベルが btex ... etex (TeX を使ったタイプセット)ではなく, 単なる文字列("x", "y", "z" など)で表示されている.
  • SVG出力(vscode のプレビューアーでの表示)で見ると全体の右上の方に表示されていることがわかる

このプログラムに1行加えていくつかのパラメータを確認してみよう.

show f,viewcentr,Spread,ShiftV;

...
>> (3,5,4)
>> (0,0,0)
>> 140
>> (297.63725,297.63725)
...

fは視点, viewcentrは視野の中心を表す. つまり, アウトプットで表示されているのは, f=(3,5,4)からviewcentr=(0,0,0)の方向(視線)を見て, viewcentrを含む平面(射影平面(視線に垂直でviewcentrを通る平面))に射影されたものが表示されている. Spreadは倍率を表す. すなわち, FeatPostにおける1は1ptを表すのではなく, 1*Spread(今の場合は 140pt)を表す. ShiftVはSpread適用後の図形を MetaPost の画面上のどこに表示するかを表す. 今の場合, MetaPost の原点(0,0)から右上に(297.63725pt,297.63725pt)だけ移動した場所に表示することを表している.

視点と射影平面の様子について, マニュアルの図(p.3 Figure 1)がわかりやすい.

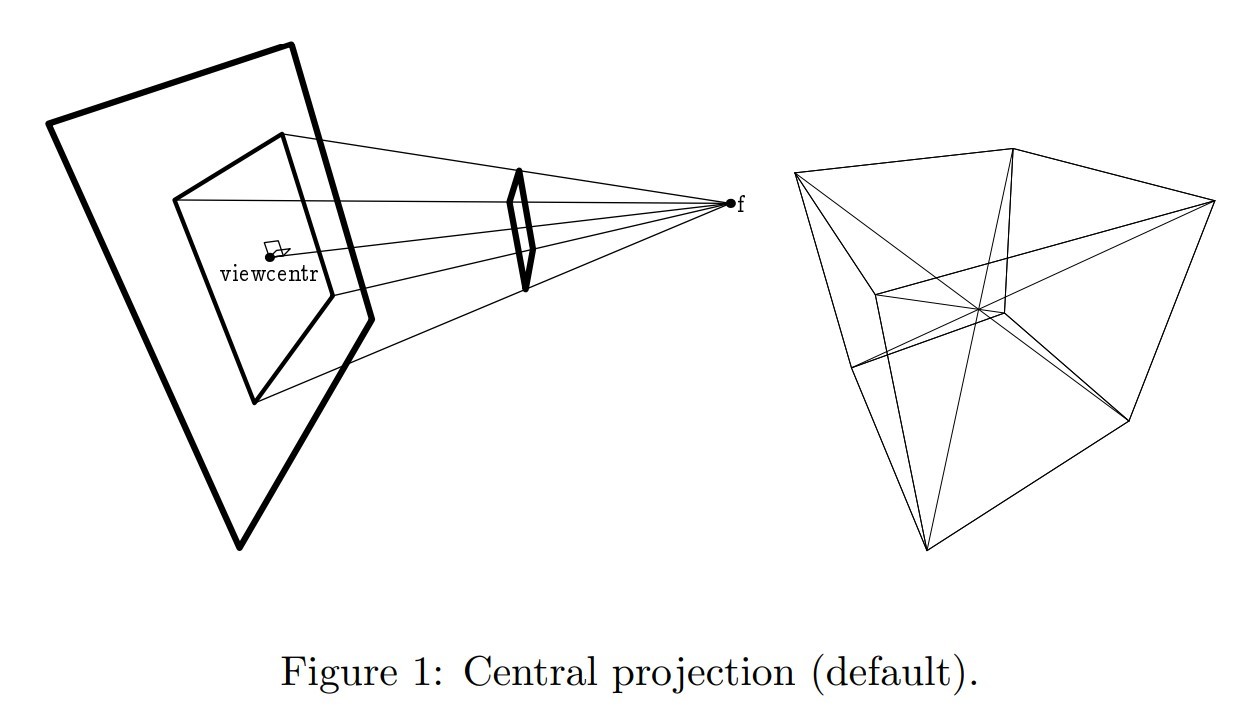
(セントラルの他, パラレルと魚眼が指定できるが, この記事では触れない.)

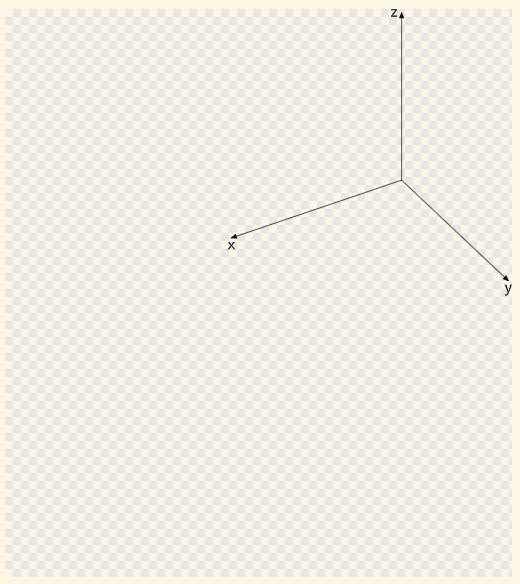
MetaPostの原点からFeatPostの射影平面の原点に明示的に矢印を引くと平行移動の様子がより明確になる.

draw (0,0)--ShiftV dashed evenly;

なぜデフォルトの設定が右上にシフトされているのか不明だが, 不要であれば ShiftV:=(0,0);とすればよい.

なお, 座標軸の描画については, cartaxes よりももう少し柔軟な orthaxes というのもある. これを使うと軸の長さに加え, ラベルを変更できる.

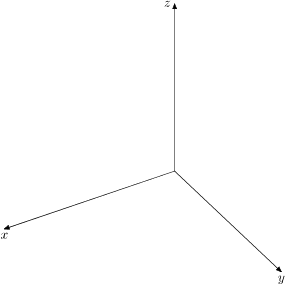
orthaxes(1,btex $x$ etex,1,btex $y$ etex,1,btex $z$ etex);

(軸の長さとラベルを引数に列挙する.)
陰線処理など, これ以上の処理が必要な場合は手書きする.

2. 直線の描画

3次元空間に線を引く. 実際には3次元空間に線を引くのではなく, 3次元空間の点から射影平面上の対応する点を算出し, その射影平面上の点を結んで線を引く. 線を引くのは MetaPostの機能でできるので, ポイントは3次元空間上の点から対応する射影平面上の点を求める部分(ここが3次元ライブラリの最も重要な部分かな, と思う). これを実現するのが rp関数である.

試しに立法体っぽい図を描いてみる.

コード
input featpost;

beginfig(3);

% ShiftV, Spread の退避,再定義
save ShiftV,Spread;
pair ShiftV;
ShiftV:=(0,0);
numeric Spread;
Spread:=72;

% 座標軸, 頂点の定義
color ax[],p[];
ax1:=(1.5,0,0);ax2:=(0,1.5,0);ax3:=(0,0,1.5);
p0:=(0,0,0);
p1:=(1,0,0);p2:=(0,1,0);p3:=(0,0,1);
p12:=(1,1,0);p23:=(0,1,1);p13:=(1,0,1);
p123:=(1,1,0.5);p231:=(0.5,1,1);p132:=(1,0.5,1);

% 立体の描画
draw rp(p0)--rp(p1) dashed evenly;
draw rp(p0)--rp(p2) dashed evenly;
draw rp(p0)--rp(p3) dashed evenly;

draw rp(p1)--rp(p12);draw rp(p1)--rp(p13);
draw rp(p2)--rp(p12);draw rp(p2)--rp(p23);
draw rp(p3)--rp(p13);draw rp(p3)--rp(p23);

draw rp(p123)--rp(p12);
draw rp(p132)--rp(p13);
draw rp(p231)--rp(p23);

draw rp(p123)--rp(p132)--rp(p231)--cycle;

drawarrow rp(p1)--rp(ax1);label.bot(btex $x$ etex,rp(ax1));
drawarrow rp(p2)--rp(ax2);label.bot(btex $y$ etex,rp(ax2));
drawarrow rp(p3)--rp(ax3);label.lft(btex $z$ etex,rp(ax3));

% DPI adj. for windows
currentpicture := currentpicture scaled (96/72);
endfig;

3次元空間上の点は color型で指定する. 陰線処理は手動(笑).

極端な話, rp関数だけあれば最低限の3次元ライブラリといえるのではないかと思う.

3. 曲線の描画

曲線についても考え方は同様で, 点を射影平面に射影してからベジェ曲線でつなぐようなイメージになる. ただ途中に射影という操作が入るので, 出来上がりに違和感が出る場合がある.

例として空間上の円について考えよう. 通常の MetaPost であれば円周上に90度ごとに点をとってベジェ曲線でつなげばそこそこの精度の円になる. しかし, 3次元空間内で同じことをしようとするとうまくいかない.

コード
beginfig(4);

% ShiftV, Spread の退避,再定義
save ShiftV,Spread;
pair ShiftV;
ShiftV:=(0,0);
numeric Spread;
Spread:=72;

% 座標軸
orthaxes(1.5,btex $x$ etex,1.5,btex $y$ etex,1.5,btex $z$ etex);

% 円の描画
color p[];
p0:=(0,0,0.5); % 中心
p1:=(1,0,0.5);p2:=(0,1,0.5);p3:=(-1,0,0.5);p4:=(0,-1,0.5);
draw rp(p1)..rp(p2)..rp(p3)..rp(p4)..cycle;
for i=1 upto 4:
  draw rp(p0)--rp(p[i]) dashed evenly;
endfor

pickup pencircle scaled 4pt;
for i=1 upto 4:
  drawdot rp(p[i]);
endfor
pickup defaultpen;

% ライブラリ関数を使った円の描画
draw rigorouscircle((0,0,0.5),(0,0,1),1) withcolor blue;

% DPI adj. for windows
currentpicture := currentpicture scaled (96/72);
endfig;

黒い線がベジェ曲線で描画した円で青い線が正確な円. かなりずれているが, これは前述のように3次元空間上の点をいったん射影平面に射影してからつないでいるため, 3次元空間内の相対的な関係が保存されていないことによる.

では各点の3次元空間内での方向を指定して描画してみたらどうか.

コード
beginfig(5);

% ShiftV, Spread の退避,再定義
save ShiftV,Spread;
pair ShiftV;
ShiftV:=(0,0);
numeric Spread;
Spread:=72;

% 座標軸
orthaxes(1.5,btex $x$ etex,1.5,btex $y$ etex,1.5,btex $z$ etex);

% 円の描画
color p[];
p0:=(0,0,0.5);
p1:=(1,0,0.5);p2:=(0,1,0.5);p3:=(-1,0,0.5);p4:=(0,-1,0.5);
p5:=(0,1,0);p6:=(-1,0,0);p7=(0,-1,0);p8:=(1,0,0);
draw rp(p1){rp(p5)}..rp(p2){rp(p6)}..rp(p3){rp(p7)}..rp(p4){rp(p8)}..cycle;

for i=1 upto 4:
  draw rp(p0)--rp(p[i]) dashed evenly;
  drawarrow rp(p[i])--rp(p[i]+0.5*p[4+i]);
endfor

pickup pencircle scaled 4pt;
for i=1 upto 4:
  drawdot rp(p[i]);
endfor
pickup defaultpen;

% ライブラリ関数を使った円の描画
draw rigorouscircle((0,0,0.5),(0,0,1),1) withcolor blue;

% DPI adj. for windows
currentpicture := currentpicture scaled (96/72);
endfig;

さっきよりはましだが, やはりずれている. 原因はセントラル射影であることによる歪みがあることや, 空間内では円であっても射影平面上では傾いた楕円であることから, それを4点で再現しようとしている点にそもそも無理がある, というあたりかもしれない.

結局一番簡単で確実なのは標本点を多くとることのような気がする.

コード
beginfig(7);

% ShiftV, Spread の退避,再定義
save ShiftV,Spread;
pair ShiftV;
ShiftV:=(0,0);
numeric Spread;
Spread:=72;

% 座標軸
orthaxes(1.5,btex $x$ etex,1.5,btex $y$ etex,1.5,btex $z$ etex);

% 円の描画
color p[];
p0:=(0,0,0.5);
p1:=(1,0,0.5);p2:=(0,1,0.5);p3:=(-1,0,0.5);p4:=(0,-1,0.5);

numeric nstep;nstep:=12;
draw rp(p1)
for i=1 upto nstep:
  ..rp((cosd(i*(360/nstep)),sind(i*(360/nstep)),0.5))
endfor
..cycle;

for i=1 upto 4:
  draw rp(p0)--rp(p[i]) dashed evenly;
endfor

pickup pencircle scaled 4pt;
for i=0 upto nstep:
  drawdot rp((cosd(i*(360/nstep)),sind(i*(360/nstep)),0.5));
endfor
pickup defaultpen;

% ライブラリ関数を使った円の描画
draw rigorouscircle((0,0,0.5),(0,0,1),1) withcolor blue;

% DPI adj. for windows
currentpicture := currentpicture scaled (96/72);
endfig;

これくらいで実用的にも問題ないと思う.

なお, 円, 楕円については以下で紹介するように, 専用の関数が用意されているので, それを使えばよい(上の例の青線(正確な円)で使用している).

4. 関数・マクロ

基本的な機能について前節までに説明したが, その他にもいろいろ便利な機能が実装されている. ここではそのうちの一部(自分で使いそうなもの)をマニュアルの区分に沿って紹介する.

4.1 基本マクロ

  • X(), Y(), Z()
    color型の各成分を求める. もともと MetaPost にある redpart, greenpart, bluepart の代替.

4.2 ベクトル演算

  • N(), conorm()
    任意のベクトルの単位ベクトル, ノルムを求める.

  • cdotprod(), ccrossprod()
    内積, 外積を求める.

  • getangle(), getcossine()
    2つのベクトルの角度, コサインを求める.

  • rotvecaroundanother()
    あるベクトルを別のベクトルの周りに回転する.

4.3 射影マクロ

  • rp()
    3次元空間の点を射影平面上の座標に変換.

  • lineintersectplan()
    直線と平面の交点を求める.

4.4 Plain 基本マクロ

(Plain というのは TeX の Plain マクロみたいな位置づけなのかな?)

  • cartaxes(), orthaxes()
    座標軸を描画する(orthaxesは軸の長さだけでなくラベルも指定できる).

  • angline(), squareangline()
    角(直角)の記号を描画する.

  • rigorouscircle(), ellipticpath()
    3次元空間内の円(楕円)を描画する.

5. 射影平面の確認

射影平面は視線(fとviewcentrを結ぶ直線)に垂直で viewcentrを通る平面, と定義される. また, 射影平面の x 軸(横軸)は xy 平面に平行に設定される(マニュアルに記載). これを実際に確認してみよう.

まずは射影平面内のベクトルを求める. デフォルトでは viewcentr が原点なので, 射影平面と xy 平面の交線は原点を通り, これが射影平面の x 軸(横軸)になる. これに注意して, 以下の手順で射影平面上の点を順次求める.

  • 法線ベクトルの xy 平面への射影 \vec{f}_{z=0} を求める.
  • これと \vec{f} の外積により射影平面内の x 方向の単位ベクトル\vec{e}_xを求める.
\vec{e}_x=\dfrac{\vec{f}\times\vec{f}_{z=0}}{|\vec{f}\times\vec{f}_{z=0}|}

FeatPostでは, ベクトルの外積は ccrossprod(), 正規化は N() を使う.

  • これを射影平面内で(\vec{f}を中心に)反時計周りに回転させることにより y 方向の単位ベクトル\vec{e}_yを求める。
\vec{e}_y=A_{\theta=90\degree,\vec{f}} \cdot \vec{e}_x

ここで, A_{\theta=90\degree,\vec{f}} は \vec{f} の周りに, 反時計回りに 90\degree 回転させる回転行列を表す. FeatPost では rotvecaroundanother() 関数を使う.

実際に求めてみる.

コード
beginfig(8);

% ShiftV, Spread の退避,再定義
save ShiftV,Spread;
pair ShiftV;
ShiftV:=(0,0);
numeric Spread;
Spread:=72;

% 座標軸の長さ
numeric axlen;
axlen:=1.5;

% 必要なベクトル等の導出
color fxy,ex,ey;

% 原点
z0=rp(viewcentr); % 記載の簡略化のため

% 視点の xy 平面への射影
fxy:=N((X(f),Y(f),0));

% 射影平面の x方向(横方向)の単位ベクトル
ex:=N(ccrossprod(f,fxy));
show ex,rp(ex);

% 射影平面の y方向(縦方向)の単位ベクトル
ey:=rotvecaroundanother(90,ex,f);
show ey,rp(ey);

% ベクトルの描画(eyの方がz軸よりも向こう側にあるので先に描画)
pickup pencircle scaled 2pt;
drawarrow z0--rp(ex) withcolor blue dashed evenly;
drawarrow z0--rp(ey) withcolor blue dashed evenly;
pickup defaultpen;
label.rt(btex $\vec{e}_x$ etex,rp(ex));
label.lft(btex $\vec{e}_y$ etex,rp(ey));

drawarrow z0--rp(fxy) dashed evenly;
label.bot(btex $\vec{f}_{z=0}/|\vec{f}_{z=0}|$ etex, rp(fxy));
orthaxes(axlen,btex $x$ etex,axlen,btex $y$ etex,axlen,btex $z$ etex);

% fベクトルの描画(画面に垂直なので, 電流とかの記法を使用)
pickup pencircle scaled 4pt;
drawdot(z0);
pickup defaultpen;
draw fullcircle scaled 8pt;
label.ulft(btex $\vec{f}$ etex, (-5,2));

% DPI adj. for windows
currentpicture := currentpicture scaled (96/72);
endfig;

\vec{e}_x, \vec{e}_y の具体的な値は show により確認できる.

show ex,rp(ex)
show ey,rp(ey)

>> (-0.8575,0.5145,0)
>> (72.0011,0)
>> (-0.29105,-0.48509,0.82462)
>> (0,72)

確かに x 方向, y 方向とも単位ベクトル(Spread=72 なので, 大きさは 72pt)になっていることが確認できる(若干誤差が生じているが気にしない(笑)).

これを用いると, rp が3次元の点を2次元平面に射影したのとは逆に, 射影平面上の点を3次元空間内に戻すことができる.

z(x,y) \Longrightarrow \vec{p} = \dfrac{x}{\text{Spread}}\cdot \vec{e}_x + \dfrac{y}{\text{Spread}} \cdot \vec{e}_x (何に使えるかは謎.)

6. 視点の変更

最後に応用として視点を移動して3次元空間内の図形の見え方の変化を確認しよう. 視点 f のデフォルトの値は (3,5,4) なので, z 座標は固定して, xy 座標を回転させて視点を移動することを考える. \vec{f}をz軸の周りに反時計周りに \theta 回転させた視点を \vec{f}' とする.

\vec{f}'=A\cdot\vec{f}, \quad A=\begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix}

適当な図形を描画して, この式に従って視点を移動してみると以下のようになる.

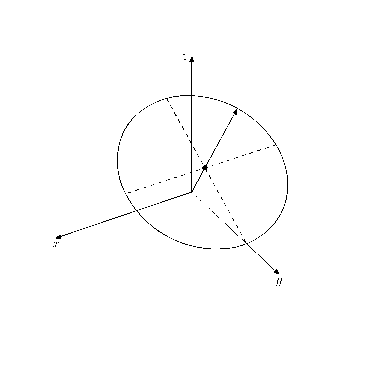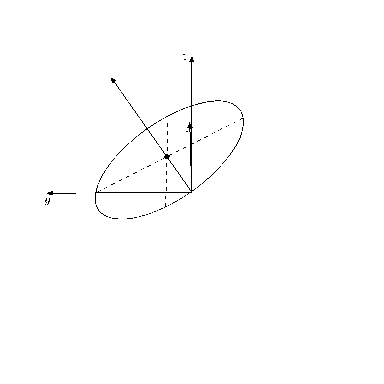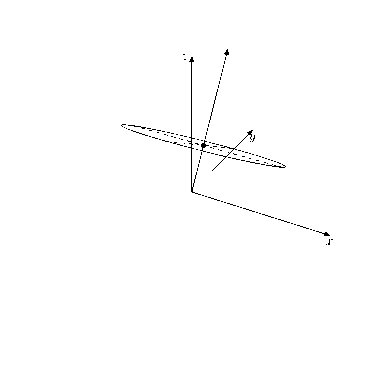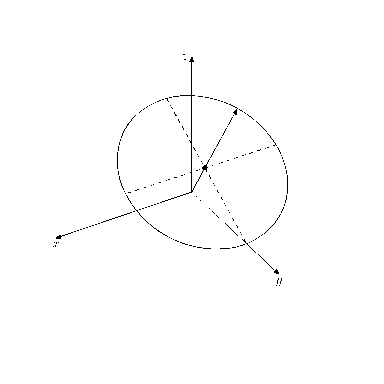
コード

各コマの出力.

prologues := 3;
outputtemplate := "%j/%6c.%o";
% outputformat := "svg";
outputformat := "png";

input featpost;

ShiftV:=(0,0);
Spread:=72;

for i=0 upto 36: %%%

beginfig(i);

% 視点の回転
theta:=i*10;
f:=(3*cosd(theta)-5*sind(theta),3*sind(theta)+5*cosd(theta),4);

% 座標軸の描画
numeric axlen;
axlen:=1.5;
orthaxes(axlen,btex $x$ etex,axlen,btex $y$ etex,axlen,btex $z$ etex);

% 円の法線ベクトル
color n[];
n0:=(0,0.25,0.25*sqrt(3));

% 円と法線ベクトルの描画
draw rigorouscircle(n0,n0,0.5*sqrt(3));
pickup pencircle scaled 4pt;
drawdot rp(n0);
pickup defaultpen;
draw rp((0,-0.5,2*Z(n0)))--rp((0,1,0)) dashed evenly;
draw rp(n0-(0.5*sqrt(3),0,0))--rp(n0+(0.5*sqrt(3),0,0)) dashed evenly;
drawarrow (0,0)--rp(3*n0);

% set bounding box
numeric blen;
blen:=2*Spread;
path bb;
bb:=(blen,blen)--(-blen,blen)--(-blen,-blen)--(blen,-blen)--cycle;

setbounds currentpicture to bb;

% DPI adj. for windows
currentpicture := currentpicture scaled (96/72);
endfig;

endfor %%%

end

julia でpngをまとめてアニメーションを作成.

import Printf.@sprintf
import Plots:Animation, buildanimation  

nframes = 36
fnames = [@sprintf("%06d.png", k) for k  in 0:nframes]   
anim = Animation("cartanim", fnames) # catanim is the folder name which contains the pngs
buildanimation(anim, "cartanim.gif", fps = 6, show_msg=false) # set a suitable fps

7. まとめ

FeatPost を試してみた. Zenn の記事用の図を描くには十分な気がした. 手軽に3次元の図が描けるのでオススメです.

Discussion