Zenn
🐙

Newton の補間公式

2024/12/26に公開
Julia
newton補間
tech

n個の標本点が与えられたとき, 以下の形の補間公式(Newton の補間公式)を導出する.

f_n(x)=c_0+c_1(x-x_1)+\cdots+c_{n-1}(x-x_1)\cdots(x-x_{n-1})

c_{k-1}\ (1\leq k\leq n) は標本点から定まる.

\begin{align*} c_0&=f[x_1]\\ c_1&=f[x_1,x_2]\\ &\vdots\\ c_{n-1}&=f[x_1,\cdots,x_{n-1}] \end{align*}

ここで, f[\cdots]は後述の差分商と呼ばれる量である.

0. 概要

与えられたn個の標本点を通る補間公式として Lagrange の補間公式が有名であるが, 別の表現として Newton の補間公式と呼ばれるものがある. Lagrange の補間公式では標本点を通ることが自明な表現になっているが, Newton の補間公式では自明でない. その代わり, 標本点が増加したときに既存のパラメータを変更する必要なく項を追加するだけで新たな補間公式が得られる, という性質がある. (ただし, 表面的な式の形が異なるだけで「2点を通る直線」, 「3点を通る放物線」など, 標本点が同じであれば Lagrange の補間公式でも Newton の補間公式でも結果として得られる曲線は同じである.)

導出については通常の数値計算の教科書(以下の参考文献等)に記載があるが, この記事で記述するような方法ではなかったのでだれかの参考になるかもしれない(単に私が知らないだけかもしれない).

参考文献

1. Newton の補間公式の導出

1.1 Newton の補間公式の性質

以下の記述では真の関数を f(x) として, 相異なる標本点を (x_1,f(x_1)), (x_2,f(x_2)), \cdots, (x_n,f(x_n)) のように抽出したとする.

Newton の補間公式では, 補間公式を 1, x-x_1, (x-x_1)(x-x_2), \cdots, (x-x_1)\cdots(x-x_{n-1}) の線形結合により求める. すなわち, 補間公式を f_n(x) とすると, 以下のような形になる.

f_n(x)=c_0+c_1(x-x_1)+\cdots+c_{n-1}(x-x_1)\cdots(x-x_{n-1})

このような形で求めるメリットは, 標本点が追加されたときに既存のパラメータ c_0, c_1, \cdots, c_{n-1} を変更する必要がないことである. 実際n+1個目の標本点が (x_{n+1},f(x_{n+1})) と与えられたとき, 補間公式は以下のような形になる.

f_{n+1}(x) = f_n(x) + c_n(x-x_1)\cdots(x-x_n)

追加された最後の項は既存の標本点(x_1,\cdots,x_n)では0になるため, この項を追加したとしても, 既存の標本点を通る, という条件に影響を与えることはない. そのため, f_{n+1}(x) を定めるためには, 追加した標本点 (x_{n+1},f(x_{n+1})) を通るように c_n を決めるだけでよい.

1.2 導出方法

(以下の導出では, 差分商が出てくるが, 差分商の定義とその性質については 3. を参照のこと. 差分商の定義とその性質がピンときてないと以下の式変形が腹落ちしにくいかもしれない.)

標本点を一個ずつ使って順番にパラメータを決める.

  1. f_1(x)=c_0 とおく.

点 (x_1,f(x_1)) を通るので, f_1(x_1)=f(x_1) より, c_0=f(x_1).

(0階の差分商を f[x_1]:=f(x_1) と定義する.)

  1. f_2(x)=f[x_1]+c_1(x-x_1) とおく.

点 (x_2,f(x_2)) を通るので, f_2(x_2)=f(x_2)=f[x_2] より,

f[x_2]=f[x_1]+c_1(x_2-x_1)

これを c_1 について解いて,

c_1 = \dfrac{f[x_2]-f[x_1]}{x_2-x_1}

(1階の差分商を f[x_1,x_2]:=\dfrac{f[x_2]-f[x_1]}{x_2-x_1} と定義する.)

  1. f_3(x)=f[x_1]+f[x_1,x_2](x-x_1)+c_2(x-x_1)(x-x_2) とおく.

点 (x_3,f(x_3)) を通るので, f_3(x_3)=f(x_3)=f[x_3] より,

f[x_3]=f[x_1]+f[x_1,x_2](x_3-x_1)+c_2(x_3-x_1)(x_3-x_2)

これを c_2 について解くため, 以下のように変形する.

\begin{align*} f[x_3]-f[x_1]&=f[x_1,x_2](x_3-x_1)+c_2(x_3-x_1)(x_3-x_2)\\ f[x_1,x_3](x_3-x_1)&=f[x_1,x_2](x_3-x_1)+c_2(x_3-x_1)(x_3-x_2)\\ f[x_1,x_3](x_3-x_1)-f[x_1,x_2](x_3-x_1)&=c_2(x_3-x_1)(x_3-x_2)\\ \dfrac{f[x_1,x_3]-f[x_1,x_2]}{x_3-x_2}(x_3-x_2)(x_3-x_1)&=c_2(x_3-x_1)(x_3-x_2) \end{align*}

標本点はすべて異なるので, 両辺を (x_3-x_2)(x_3-x_1) で割って,

c_2 = \dfrac{f[x_1,x_3]-f[x_1,x_2]}{x_3-x_2}

(2階の差分商を f[x_1,x_2,x_3]:=\dfrac{f[x_1,x_3]-f[x_1,x_2]}{x_3-x_2} と定義する.)

  1. 同様の変形を繰り返し行うことによって, c_{k-1}=f[x_1,\cdots,x_k](1\leq k\leq n)

(k-1階の差分商を f[x_1,\cdots,x_k]=\dfrac{f[x_1,\cdots,x_{k-2},x_k]-f[x_1,\cdots,x_{k-2},x_{k-1}]}{x_k-x_{k-1}} と定義する.)

最終的に以下の表式が得られる.

(x_1,f(x_1)), (x_2,f(x_2)), \cdots, (x_n,f(x_n)) を通る Newton の補間公式:

\begin{align*} f_n(x) &= f[x_1]+f[x_1,x_2](x-x_1)+\cdots\\ &+f[x_1,\cdots,x_n](x-x_1)\cdots (x-x_{n-1}) \end{align*}

ここで, f[x_k]:=f(x_k)\ (1\leq k\leq n) である.

2. 差分商の性質

標本点については前節と同様に定義されているとする.

2.1 差分商の定義

差分商の定義について再度まとめる.

  1. 0階の差分商:
\begin{align*} f[x_k]&=f(x_k)\\ &(1\leq k\leq n) \end{align*}
  1. 1階の差分商:
\begin{align*} f[x_i, x_j]&=\dfrac{f[x_j]-f[x_i]}{x_j-x_i}\\ &(i\neq j, 1\leq i,j \leq n) \end{align*}
  1. k-1階の差分商:
\begin{align*} f[x_1,\cdots,x_k]&=f[\cdots,x_i,\cdots,x_j,\cdots]\\ &=\dfrac{f[\cdots,x_j,\cdots]-f[\cdots,x_i,\cdots]}{x_j-x_i}\\ &(i\neq j, 1\leq i,j \leq k, 2\leq k\leq n) \end{align*}

(分子は x_i を含まない k-2 階の差分商から x_j を含まない k-2 階の差分商を引いたもの(x_i, x_j 以外の引数は共通). このとき分母は x_j -x_i になる.)

2.2 差分商の性質

  1. 差分商の別の表現

k-1階の差分商(2\leq k\leq n)の別の表現

\begin{align*} f[x_1,\cdots,x_k] &=\dfrac{x_1}{(x_1-x_2)(x_1-x_3)\cdots(x_1-x_k)}\\ &+\dfrac{x_2}{(x_2-x_1)(x_2-x_3)\cdots(x_2-x_k)}\\ &+\cdots\\ &+\dfrac{x_{k-1}}{(x_{k-1}-x_1)\cdots(x_{k-1}-x_{k-2})(x_{k-1}-x_k)}\\ &+\dfrac{x_k}{(x_k-x_1)\cdots(x_k-x_{k-2})(x_k-x_{k-1})}\\ &=\sum_{i=1}^k \dfrac{x_i}{\prod_{j\neq i}^k (x_i -x_j)} \end{align*}

証明は帰納法により簡単に示せる(こちらなどを参照のこと).

  1. 対称性

差分商は引数の順序によらず同じ値をとる(上の性質1. の表現から明らか).

(もちろん標本点が異なれば得られる補間公式も異なる. 標本点が同じであれば標本点の順序によらず補間公式は同じになる.)

3. 数値例

実際に補間公式を作成し, プロットしてみる.

3.1 概要

区間[0,1]の適当な関数から標本点をランダムに抽出し, 標本点を増やしながら補間公式がどのように求まってゆくかをグラフで確認する.

手順:

  • 標本点抽出用の関数を準備
    以下の関数からランダムに標本点を抽出する.
f(x)=0.5+(x-0.02)*(x-0.25)*(x-0.5)*(x-0.75)*(x-0.98)

  • Newton の補間公式を返す関数
    • 差分商(補間公式の係数)を求める関数を作成
    • 標本点が零点となるような関数を返す関数を作成
    • 上をまとめて Newton の補間公式を作成
  • 求めた Newton の補間公式を順番にプロットし, アニメーションを作成

3.2 差分商を返す関数

標本点の数を n とすると, 考えうる差分商のパターンは, 各標本点が差分商の引数に含まれるか含まれないかを考えればよく, 2^n 通り(差分商は引数の順序に依存しない). しかし Newton の補間公式に必要なのはそのうちの一部のみ. 例えば, f[x_1,x_2,x_3,x_4] の計算に必要なのは f[x_1,x_2,x_3] と f[x_1,x_2,x_4] のみで他の2階の差分商(f[x_1,x_3,x_4],f[x_2,x_3,x_4])は必要ない.

f[x_1,x_2,x_3,x_4]=\dfrac{f[x_1,x_2,x_4]-f[x_1,x_2,x_3]}{x_4 - x_3}

このように計算に必要な差分商をリストアップすると以下のようになる(全部で n(n+1)/2 通りの差分商が必要).

1 2 3 4
1 f[x_1] f[x_2] f[x_3] f[x_4]
2 f[x_1,x_2] f[x_1,x_3] f[x_1,x_4]
3 f[x_1,x_2,x_3] f[x_1,x_2,x_4]
4 f[x_1,x_2,x_3,x_4]

例えば3行4列の f[x_1,x_2,x_4] に注目すると, これを計算するのに必要なのは f[x_1,x_2] と f[x_1,x_4].

f[x_1,x_2,x_4]=\dfrac{f[x_1,x_4]-f[x_1,x_2]}{x_4 - x_2}

すなわち前の行の対角成分と前の行の自分の列の要素を見ればよい.
なお, 上の表は計算に必要な差分商で, 最終的に Newton の補間公式に必要なのは対角成分のみ.

これを求める関数は以下のように実装できる.

# difference quotient 差分商
# 標本点から f[x_1], f[x_1,x_2], ... を返す
function dq(f,x)
  n=length(x)
  c=zeros(n,n)
  if n==1
    c[1,1]=f(x[1])
  else
    for j in 1:n
      c[1,j]=f(x[j])
    end
    for i in 2:n
      for j in i:n
        # 全部の引数パターンの差分商は不要
        # 各階数で引数がひとつだけ異なるものが必要
        # 分子の最初の項はjでループ, 後ろの項は対角成分
        # (これで必要な分だけ差分商を生成できる)
        c[i,j]=(c[i-1,j]-c[i-1,i-1])/(x[j]-x[i-1])
      end # for j
    end # for i
  end # if
  # newton 補間に必要なのは対角成分の差分商のみ
  return diag(c)
end # dq

3.3 零点多項式を返す関数

ここで零点多項式と呼んでいるのは標本点を零点とするような多項式で具体的には 1, x-x_1, (x-x_1)(x-x_2), \cdots を表すことにする. 関数を返す関数なので、julia の無名関数を使う. また, 結果は関数の配列として返す.

実装は以下のとおり.

# 標本点から 1,(x-x_1),(x-x_1)(x-x_2)などの
# 関数を配列で返す
function poly(x)
  n=length(x)
  # 多項式の関数を入れる入れ物
  # (任意の型のn要素1次元配列)
  res=Array{Any,1}(undef,n)
  res[1]=t->1
  if 1<n
    for i in 2:n
      res[i]=function(t)
        tmp=1
        for j in 2:i
          tmp*=(t-x[j-1])
        end
        return tmp
      end # function
    end # for i
  end # if
  return res
end # poly
  • 関数の配列は本当は Any ではなくちゃんと型を指定して作りたかったが, 関数の型の指定の仕方がよくわからなかったので Any にしている.
  • x-x_i の掛け算を作るところを泥臭くループにしてるけど, もう少し洗練された書き方はできないものか.

3.3 Newton の補間公式を返す関数

Newton の補間公式を最高次(n-1次)の関数のみでなく, 0次の関数(定数)からすべて求める(後でプロットするため). これは上で定義した関数(dq, poly)を使うと簡単に作成できる(上の零点多項式のループのところで一気にやってもよかったが, ごちゃごちゃする感じがしたので分けた).

実装は以下のとおり.

# 0次からn-1次までの newton の補間公式を
# 配列で返す
# f: 標本抽出用の関数
# x: 標本点の x 座標
function newton(f,x)
  n=length(x)
  c=dq(f,x)
  p=poly(x)
  # 補間多項式の関数を入れる入れ物
  # (任意の型のn要素1次元配列)
  res=Array{Any,1}(undef,n)
  for i in 1:n
    # newton の補間公式を構築
    res[i]=function(t)
      tmp=0
      for j in 1:i
        tmp+=c[j]*p[j](t)
      end
      return tmp
    end # function
  end # for i
  return res
end # newton
  • これも Newton の補間公式を作ってるループのところが泥臭い感じがする. Haskell とかならもっとカッコよく書けそう.

3.4 アニメーション GIF の作成

関数 f(x) のグラフに上で求めた Newton の補間公式を0次から順番にプロットしてアニメーションGIFにする.

実装は以下のとおり.

function main()
  Random.seed!(202412)
  n=6 # number of samples
  xi=rand(n)
  yi=f.(xi)

  p=newton(f,xi)

  # 標本点抽出用の関数をプロット
  # Newton の補間公式はこの関数上に上書きプロットする
  x=range(0,1,length=100)
  y=f.(x)
  plt0=plot(x,y,label="f",legend=:bottomleft)
  savefig("f.png")

  # Newton の補間公式をプロット
  # plts[i] にplt0をコピーするときは
  # deepcopy にして別のプロットにする
  plts=Array{Any,1}(undef,n)
  for i in 1:n
    plts[i]=deepcopy(plt0)
    scatter!(plts[i],xi[1:i],yi[1:i],label="")
    yp=p[i].(x)
    plot!(plts[i],x,yp
          ,ylims=ylims(plt0)
          ,label=string("p[",i,"]")
          ,legend=:bottomleft)
  end # for i

  # アニメーションGIFの作成
  anim=Animation()
  for i in 1:n
    frame(anim,plts[i])
  end
  gif(anim,"newton.gif",fps=1)
end # main
  • 標本点は6個にして全部使うと元の関数(5次関数)を再現できるようにした. また, 再現性を確保するため, 乱数シードを指定している.
  • 元の関数 f(x) を描画しているのが plt0 で, 続くループの中でこのグラフに上書きして各 Newton の補間公式をプロットしている.
  • plot の配列も型がよくわからなかったので, Any で準備している.
  • plot は deepcopy しないで代入するだけだと参照がコピーされるようでループの中で同じグラフに上書きされてしまう.
  • y軸が変わるとアニメーションが見づらくなるので, ylims で元の関数のグラフのy軸と同じになるようにしている.
  • plot の配列ができればアニメーションGIFは簡単に作成できる(最後の5行).

3.5 コードの全体像

コードの全体像は以下のとおり(上で記載したものは省略している).

prg.jl
module Prg

using Plots
using Random
using LinearAlgebra

function f(x)
  return 0.5+(x-0.02)*(x-0.25)*(x-0.5)*(x-0.75)*(x-0.98)
end

# difference quotient 差分商
# 標本点から f[x_1], f[x_1,x_2], ... を返す
function dq(f,x)
...
end # dq

# 標本点から 1,(x-x_1),(x-x_1)(x-x_2)などの
# 関数を配列で返す
function poly(x)
...
end # poly

# 0次からn-1次までの newton の補間公式を
# 配列で返す
# f: 標本抽出用の関数
# x: 標本点の x 座標
function newton(f,x)
...
end # newton

function main()
...
end # main

end # module Prg

using .Prg

3.6 結果

完成したアニメーションGIF

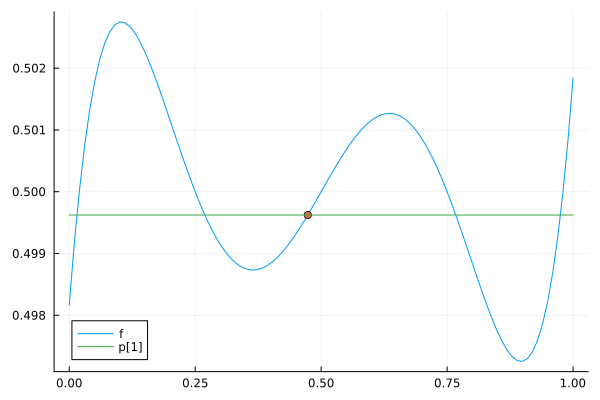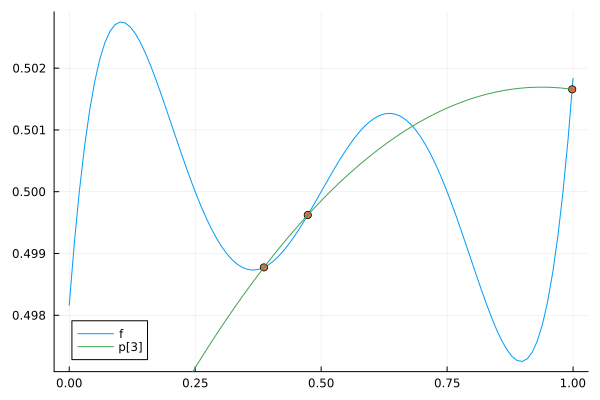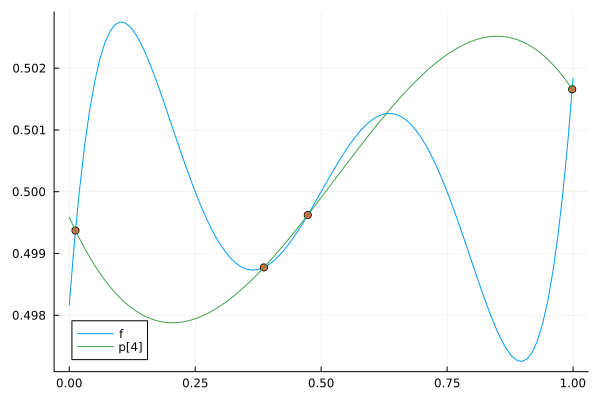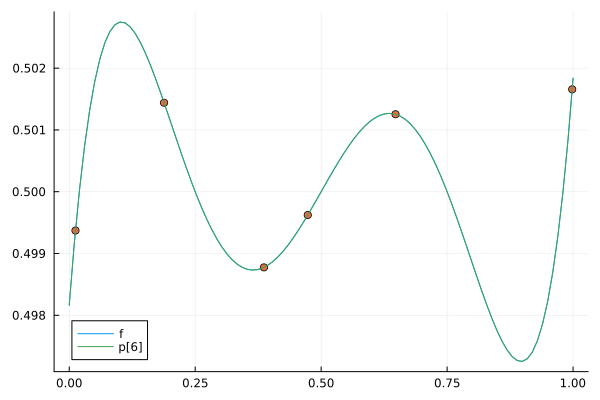
標本点が増えるにしたがって, 補間曲線の次数も上がり元の関数に近づいていることがわかる(標本点が6個になると当然元の関数に一致する).

4. まとめ

参考文献やネットの検索で出てくる導出方法はもっと洗練されたものであるが, 上で挙げた方法も Newton 補間のイメージをつかむ, という意味では悪くないと思った. 誰かの参考になれば幸いです.

Discussion