自分で実装するときの備忘として記載. C#での実装(インデックスベースが0). 内容自体はちまたにありふれたもの.
区間の指定に区間の右端のインデックスを使用するコンベンションで記載(x_{i-1}<x\le x_i のとき x の含まれる区間を i とする).
与えられた x に対してそれが含まれる区間を求める2分探索の部分の説明をちょっと詳しく記載.
0. 参考文献
- [改訂新版]C言語による標準アルゴリズム事典
1. 補間の条件
n 個の標本点を (x_i,y_i) \ (i=0,\cdots,n-1) とし, 各区間を3次関数 f_i(x) \ (i=1,\cdots,n-1) で補間する.
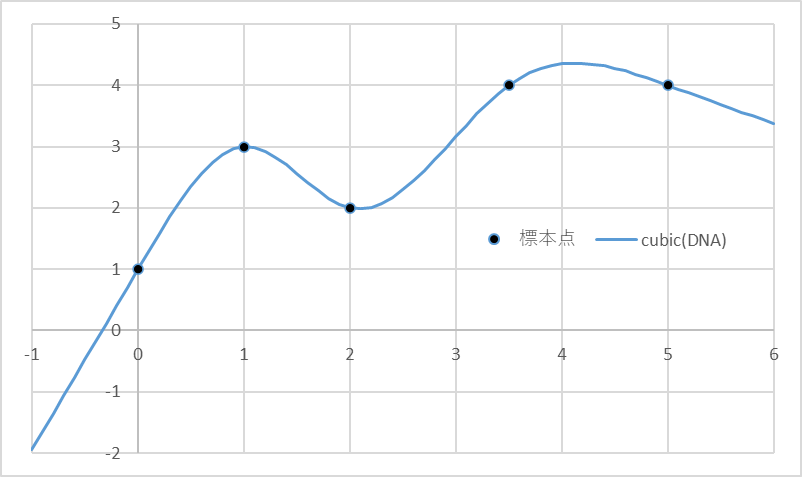
上図は n=5 の場合の例. 補間関数は3次関数なので決定すべきパラメータは各区間で4, 区間の数が n-1 なので, 合計 4(n-1) のパラメータを決める必要がある. 条件を以下のように設定すると条件の数とパラメータの数が一致し, 補間関数が一意的に定まる.
- 標本点を通る(2(n-1)個の条件):
\begin{align*}
f_i(x_{i-1})&=y_{i-1}\\
f_i(x_i)&=y_i
\end{align*}
(i=1,\cdots,n-1 )
- 標本点で傾きが一致(1階の導関数が連続)(n-2個の条件):
(i=1,\cdots,n-2 )
- 標本点で曲率が一致(2階の導関数が連続)(n-2個の条件):
f''_i(x_i)=f''_{i+1}(x_i)
(i=1,\cdots,n-2 )
- 端点の曲率(2階の導関数)が0(2個の条件):
f_1(x_0)=0, f_{n-1}(x_{n-1})=0
※ 4番目が自然スプラインの「自然」の条件
2. 定式化
2.1 定式化の方針
普通に考えると補間関数を f(x)=ax^3+bx^2+cx+d のようにおけばよいが, ここでは先を見越して標本点における2階の導関数の値を z'_i \ (i=0,\cdots,n-1) とおき(ダッシュは後の式変形の都合で付けたもので微分の記号ではない), 2階の導関数を積分して補間関数を求めることにする.
各区間の2階の導関数は1次関数なので, パラメータは 2(n-1) 個. これに上の 3. の条件を使うと残り 2(n-1)-(n-2) = n 個. これをn個の z'_i とおいていることになる. 残りのパラメータは積分2回分の積分定数だから 2(n-1) 個で, 合計 3n-2 個のパラメータが残る. これに対して残っている条件は 1. が 2(n-1)個, 2. が n-2個, 4. が2個なので, 合計 3n-2 でありちょうど一致している.
2.2 2階の導関数とその積分
標本点における2階の導関数の値を z'_i \ (i=0,\cdots,n-1) とおく. 2階の導関数は1次関数なので, 各区間の2階の導関数はこれらの点を線形補間で結んだものになる. したがって,
\begin{align*}
f''_i(x)&=\dfrac{z'_{i-1}(x_i-x)+z'_i(x-x_{i-1})}{\Delta x_i}\\
\Delta x_i &:= x_i-x_{i-1}
\end{align*}
これを積分して,
\begin{align*}
f'_i(x)&=\dfrac{1}{\Delta x_i}\Big[
-\dfrac{z'_{i-1}}{2}(x_i-x)^2
+\dfrac{z'_i}{2}(x-x_{i-1})^2
\Big]+C_{1i}\\
f_i(x)&=\dfrac{1}{\Delta x_i}\Big[
\dfrac{z'_{i-1}}{6}(x_i-x)^3
+\dfrac{z'_i}{6}(x-x_{i-1})^3
\Big]+C_{1i}x+C_{2i}\\
\end{align*}
ここで記号の簡略化のため, z_i:=z'_i/6 とする.
\begin{align*}
f'_i(x)&=\dfrac{1}{\Delta x_i}[
-3z_{i-1}(x_i-x)^2+3z_i(x-x_{i-1})^2
]+C_{1i}\\
f_i(x)&=\dfrac{1}{\Delta x_i}[
z_{i-1}(x_i-x)^3
+z_i(x-x_{i-1})^3
]+C_{1i}x+C_{2i}\\
\end{align*}
2.3 標本点を通る, という条件を加味
標本点を通るという条件(上述の 1. の条件)より, f_i(x_{i-1})=y_{i-1}, f_i(x_i)=y_i (i=1,\cdots,n-1) であるから,
\begin{align*}
y_{i-1}&=z_{i-1}\Delta x_i^2+C_{1i}x_{i-1}+C_{2i} \\
y_i &=z_i\Delta x_i^2+C_{1i}x_i+C_{2i}
\end{align*}
y_i-y_{i-1} より,
C_{1i}=\dfrac{\Delta y_i}{\Delta x_i}-\Delta x_i (z_i-z_{i-1})
x_i y_{i-1}-x_{i-1} y_i より,
C_{2i}=\dfrac{x_i y_{i-1}-x_{i-1} y_i}{\Delta x_i}
-\Delta x_i (x_i z_{i-1}-x_{i-1} z_i)
これらを代入して,
\begin{align*}
f'_i(x)&=
z_{i-1}\Big[-3\dfrac{(x_i-x)^2}{\Delta x_i} + \Delta x_i\Big]
+z_i\Big[3\dfrac{(x-x_{i-1})^2}{\Delta x_i} - \Delta x_i\Big]
+\dfrac{\Delta y_i}{\Delta x_i} \\
f_i(x)&=
z_{i-1}\Big[\dfrac{(x_i-x)^3}{\Delta x_i} - (x_i-x) \Delta x_i\Big]
+z_i\Big[\dfrac{(x-x_{i-1})^3}{\Delta x_i} - (x-x_{i-1})\Delta x_i\Big] \\
&\quad +\dfrac{(x_i-x)y_{i-1}+(x-x_{i-1})y_i}{\Delta x_i}
\end{align*}
標本点を通る, という 2(n-1) 個の条件から 2(n-1) 個の積分定数 C_{1i}, C_{2i} を消去できた.
2.4 標本点で傾きが一致, という条件を加味
標本点で傾きが一致する(上述の 2. の条件)を考える. まず, f'_{i+1}(x) の式を確認しておく. f'_i(x) の式で i を一つずらして,
f'_{i+1}(x) =
z_i\Big[-3\dfrac{(x_{i+1}-x)^2}{\Delta x_{i+1}} + \Delta x_{i+1}\Big]
+z_{i+1}\Big[3\dfrac{(x-x_i)^2}{\Delta x_{i+1}} - \Delta x_{i+1}\Big]
+\dfrac{\Delta y_{i+1}}{\Delta x_{i+1}}
f'_i(x_i), f'_{i+1}(x_i) を計算すると,
\begin{align*}
f'_i(x_i)&=\Delta x_i z_{i-1} +2 \Delta x_i z_i + \dfrac{\Delta y_i}{\Delta x_i}\\
f'_{i+1}(x_i)&=-2\Delta x_{i+1} z_i-\Delta x_{i+1} z_{i+1} +\dfrac{\Delta y_{i+1}}{\Delta x_{i+1}}
\end{align*}
標本点で傾きが一致する, というのは f'_i(x_i)=f'_{i+1}(x_i) \ (i=1,\cdots,n-2) だから,
\Delta x_i z_{i-1} +2 (\Delta x_i +\Delta x_{i+1}) z_i +\Delta x_{i+1} z_{i+1}
=\dfrac{\Delta y_{i+1}}{\Delta x_{i+1}}-\dfrac{\Delta y_i}{\Delta x_i}
これに自然スプラインの条件 z_0=z_{n-1}=0 (上述の 4. の条件) を使って行列形式に書き直すと, 以下のようになる.
\begin{pmatrix}
2(\Delta x_1+\Delta x_2)&\Delta x_2&0&&&& \\
\Delta x_2&2(\Delta x_2+\Delta x_3)&\Delta x_3&&&& \\
0&\Delta x_3&2(\Delta x_3+\Delta x_4)&&&0& \\
&&&&&&\\
&&\ddots&\ddots&\ddots&& \\
&&&&&&\\
&0&&&2(\Delta x_{n-4}+\Delta x_{n-3})&\Delta x_{n-3}&0\\
&&&&\Delta x_{n-3}&2(\Delta x_{n-3}+\Delta x_{n-2}&\Delta x_{n-2}\\
&&&&0&\Delta x_{n-2}&2(\Delta x_{n-2}+\Delta x_{n-1})
\end{pmatrix}
\begin{pmatrix}
z_1\\
z_2\\
z_3\\
\vdots\\
\vdots\\
z_{n-4}\\
z_{n-3}\\
z_{n-2}\\
\end{pmatrix}
=
\begin{pmatrix}
\dfrac{\Delta y_2}{\Delta x_2}-\dfrac{\Delta y_1}{\Delta x_1}\\
\vdots\\
\vdots\\
\vdots\\
\dfrac{\Delta y_{n-1}}{\Delta x_{n-1}}-\dfrac{\Delta y_{n-2}}{\Delta x_{n-2}}
\end{pmatrix}
この連立方程式を z_i について解けばよい. 連立1次方程式なので, 何等かの線形ライブラリ(行列演算など)を使えばよいが, この問題のように3重対角化された連立方程式の場合には公式のようなものが存在する.
ただ連立方程式を解くだけなのに名前がついているのも不思議な感じがする. やっていることは小さい方のインデックスから順番に解いてゆき, それを公式の形にまとめているだけである.
一方, 冒頭で参考文献として挙げた[改訂新版]C言語による標準アルゴリズム事典では, ガウスの消去法(掃き出し法)で解いている. ネットを軽く見てもこのコードをそのまま使っているサイトは結構ある. 配列を上書きしながら使いまわしているので, メモリー効率は多少いいかもしれない. ただし, 解説がないと何をやっているのかわかりにくいので, 本稿では TDMA を採用することにする.
2.5 3重対角化された連立方程式の解
記号を簡略化して, 以下のような連立方程式を考える.
\begin{pmatrix}
b_1&c_1&0&\\
a_2&b_2&c_2&\\
0&a_3&b_3&&&0&\\
&&&&&&\\
&&\ddots&\ddots&\ddots&& \\
&&&&&&\\
&0&&&b_{n-4}&c_{n-4}&0\\
&&&&a_{n-3}&b_{n-3}&c_{n-3}\\
&&&&0&a_{n-2}&b_{n-2}
\end{pmatrix}
\begin{pmatrix}
z_1\\
z_2\\
z_3\\
\vdots\\
z_{n-4}\\
z_{n-3}\\
z_{n-2}
\end{pmatrix}
=
\begin{pmatrix}
d_1\\
d_2\\
d_3\\
\vdots\\
d_{n-4}\\
d_{n-3}\\
d_{n-2}
\end{pmatrix}
上から順番に代入してゆくことにより, この連立方程式は以下のように解くことができる.
\begin{align*}
z_i&=P_i z_{i+1}+Q_i, \quad i=1,\cdots,n-2\\
z_{n-1}&=0\\
&\\
P_0&=0\\
P_i&=\dfrac{-c_i}{a_iP_{i-1}+b_i}, \quad i=1,\cdots,n-3\\
P_{n-2}&=0\\
&\\
Q_0&=0\\
Q_i&=\dfrac{-a_iQ_{i-1}+d_i}{a_iP_{i-1}+b_i}, \quad i=1,\cdots,n-2\\\\
\end{align*}
プログラムに実装する際には最初に P_i, Q_i をフォワードに求め, それを使って z_i をバックワードに求めればよい.
前節までの式との対応は以下のとおり.
\begin{align*}
a_i&=\Delta x_i\\
b_i&=2(\Delta x_i+\Delta x_{i+1})\\
c_i&=\Delta x_{i+1}\\
d_i&=\dfrac{\Delta y_{i+1}}{\Delta x_{i+1}}-\dfrac{\Delta y_i}{\Delta x_i}\\
\end{align*}
2.6 結果のまとめ
ここまでの結果をまとめると以下のようになる(f_i(x) の2行目は参考文献で実装されている形であり, べき乗がなく計算回数が少ない形になっており, 計算機的な意味で簡略化されている.)
\begin{align*}
f_i(x)
&=
z_{i-1}\Big[\dfrac{(x_i-x)^3}{\Delta x_i} - (x_i-x) \Delta x_i\Big]
+z_i\Big[\dfrac{(x-x_{i-1})^3}{\Delta x_i} - (x-x_{i-1})\Delta x_i\Big]\\
&\quad +\dfrac{(x_i-x)y_{i-1}+(x-x_{i-1})y_i}{\Delta x_i}\\
&=\Big[
\Big\{\dfrac{z_i-z_{i-1}}{\Delta x_i}(x-x_{i-1})+3z_{i-1}\Big\}(x-x_{i-1})\\
&\quad +\dfrac{\Delta y_i}{\Delta x_i}-(2z_{i-1}+z_i)\Delta x_i\Big](x-x_{i-1})+y_{i-1},
\quad i=1,\cdots,n-1\\
\\
&\\
z_0&=0, z_{n-1}=0\\
&\\
z_i&=P_i z_{i+1}+Q_i, \quad i=1,\cdots,n-2\\
&\\
P_0&=0\\
P_i&=\dfrac{-\Delta x_{i+1}}{\Delta x_iP_{i-1}+2(\Delta x_i+\Delta x_{i+1})}, \quad i=1,\cdots,n-3\\
P_{n-2}&=0\\
&\\
Q_0&=0\\
Q_i&=\dfrac
{-\Delta x_iQ_{i-1}+
\dfrac{\Delta y_{i+1}}{\Delta x_{i+1}}-\dfrac{\Delta y_i}{\Delta x_i}
}
{\Delta x_iP_{i-1}+2(\Delta x_i+\Delta x_{i+1})}
, \quad i=1,\cdots,n-2\\\\
\end{align*}
2.7 外挿部分
x_0 と x_{n-1} の外側については特に制約はないのでそれぞれの場面で都合の良いものを採用すればよいが, ここでは直線で補外することにする.
\begin{align*}
f_0(x)&=f'_1(x_0)(x-x_0)+y_0\\
&=(-z_1\Delta x_1+\dfrac{\Delta y_1}{\Delta x_1})(x-x_0)+y_0\\
f_\infty(x)&=f'_{n-1}(x_{n-1})(x-x_{n-1})+y_{n-1}\\
&=(z_{n-1}\Delta x_{n-1}+\dfrac{\Delta y_{n-1}}{\Delta x_{n-1}})(x-x_{n-1})+y_{n-1}\\
\end{align*}
自然スプラインの場合, 端点での曲率(2次の導関数)が0なので直線で外挿すれば, 端点で傾きも曲率も連続になるので, ある意味で自然な選択であるといえる.
ちなみに参考文献では両端の3次関数をそのまま外挿部分に使用するようになっている(特に別の関数を指定したりはしていない).
2.8 区間の特定
実際に補間計算を行う場合, 求めたい点がどの区間にあるかを探索する必要がある. 参考文献では2分探索により区間を特定している. ここでも2分探索を採用することにする. ただし, 区間を指定するインデックスのコンベンション(x_{i-1}<x\le x_i のとき x の含まれる区間を i とする)に注意する.
以下のようなロジックを2分探索で実装する. 所与の x に対して,
\begin{align*}
0 &\quad\text{for} \ x\le x_0\\
\infty &\quad\text{for} \ x_{n-1}<x\\
i &\quad\text{for} \ x_{i-1}<x\le x_i
\end{align*}
これらに応じて f_0(x), f_\infty(x), f_i(x) を呼び出す(実際の実装では \infty を返す代わりに n を返すことにする.)
ロジックの流れは以下のとおり.
-
x\le x_0 のとき, 0 を返す(終了)
-
x_{n-1}<x のとき, n を返す(終了)
-
i=0, j=n-1 とする
-
i<jのとき,
4.1 k=(i+j)/2(切り捨て)とする
4.2 x\le x_k のとき, j=k とする
4.3 x_k<x のとき, i=k+1 とする
4.4 4. に戻る
-
i を返す(終了)
i は x が含まれる区間の右端のインデックスになっているので, 補間に使用する関数は f_i(x) になる.
このロジックでうまく探索できることはいくつか具体的な場合を考えるとイメージしやすい. 以下に図を用いた説明を記載しておく.
図解
より具体的に考えるために, 4. のループが終了する直前の状況を考える.
最初に x_0\le x \le x_{n-1} の場合, すなわち, x が標本点の内側にある場合を考える.
上の 4. のループが終了するのはi=jになる場合で, その直前の状態として以下の2つの場合が考えられる. (図中の数直線上の i, j などはそれぞれ x_i, x_j を意味する(以下同様).)
(1) i, j が隣り合っているとき(1つ離れている)
(2) i, j が2つ離れているとき

(1) のとき, k=(i+j)/2=i(切り捨てのため).

このとき, x \ (x_i\le x \le x_j の場所に応じて以下の2パターンが考えられる.
(1-a) x\le x_i, つまり x=x_i のとき, x\le x_k だから j=k より, i=j
(1-b) x_i<x\le x_{i+1}, つまり x_i<x\le x_j のとき, x_k<x だから i=k+1 より, i=j

いずれの場合も x を含む区間の右端のインデックスが i になる.
(2) のとき, k=(i+j)/2=i+1=j-1.

このとき, x の場所に応じて, 以下の3パターンが考えられる.
(2-a)(x=x_i) は (1-a) に帰着
(2-b) も (1-b) に帰着
(2-c) は x\le x_k だから i=k+1 より, i=j.

この場合も (1) と同様最終的に x を含む区間の右端のインデックスが i になる.
(3) i と j がもっと離れているときもループにより最終的に上の2つに帰着する.
例えば, 3つ離れているとき,

j=k もしくは i=k+1 で, どちらの場合も (1) に帰着する.
4つ離れているとき,
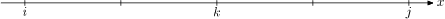
j=k のときは (2), $i=k+1 のときは (1) に帰着する.
最後に x が標本点の外側(外挿)の場合を考える. 上に記載したロジックでは先に外挿の場合を除いて2分探索を実行しているが, 試しにそのまま2分探索を適用してみる.
x<x_0 のとき, j が i に近づいてゆき, 最終的に j=i=0 となる. また, x_{n-1}<x のとき, i が j に近づいてゆき, 最終的に i=j=n-1 となる. この場合, そのまま n-1 を返してしまうと x_{n-2}<x\le x_{n-1} の場合と区別がつかなくなり, 両者で別の関数を使用したい場合は別途対応が必要となる.
上のロジックでは外挿の場合, 特別な関数(直線)を使うことにしているため, 最初に if文で外挿の場合を分離している.
3. 実装(C#, ExcelDNA)
上で導出した式をそのまま実装すればよい. 標本点と求めたい点の x 座標を与えると, 補間後の y 座標を返す, というのがやりたいことであるが, 2階の導関数の値 \{z_i\} は標本点に対して決まるものなので, 同じ標本点に対して何度も補間計算をするのであれば, この部分だけ独立させた方が効率的である. そこで, 以下のように2つの関数に分けて実装することにする.
\begin{align*}
\{z_i\}&=g(\{x_i\},\{y_i\})\\
y&=f(\{x_i\},\{y_i\},\{z_i\},x)
\end{align*}
参考文献の maketable 関数が g に対応し, spline 関数に対応する. 以下のコードではそれぞれ interp_cubic_ 関数, interp_cubic 関数に対応する.
コード
ExcelDna64.dna
<DnaLibrary RuntimeVersion="v4.0" Language="CS" >
<![CDATA[
public class Udf
{
public static double[,] interp_cubic_(double[,] x, double[,] y)
{
int n=x.GetLength(0);
var z=new double[n,1];
var p=new double[n];
var q=new double[n];
p[0]=0;q[0]=0;
for(int i=1;i<n-1;i++){
p[i]=-(x[i+1,0]-x[i,0])
/((x[i,0]-x[i-1,0])*p[i-1]+2*(x[i+1,0]-x[i-1,0]));
q[i]=(-(x[i,0]-x[i-1,0])*q[i-1]
+(y[i+1,0]-y[i,0])/(x[i+1,0]-x[i,0])
-(y[i,0]-y[i-1,0])/(x[i,0]-x[i-1,0]))
/((x[i,0]-x[i-1,0])*p[i-1]+2*(x[i+1,0]-x[i-1,0]));
}
p[n-2]=0;
for(int i=n-2;0<i;i--){
z[i,0]=p[i]*z[i+1,0]+q[i];
}
return z;
}
public static double interp_cubic(double[,] x, double[,] y, double[,] z, double xx)
{
int n=x.GetLength(0);
int i=0, j=n-1,k;
if(xx<x[0,0]){
i=0;
}else if(x[n-1,0]<xx){
i=n;
}else{
while (i<j){
k=(i+j)/2;
if(xx<=x[k,0]){
j=k;
}else{
i=k+1;
}
}
}
double res;
if(i==0){
res=(-z[1,0]*(x[1,0]-x[0,0])+(y[1,0]-y[0,0])/(x[1,0]-x[0,0])
)*(xx-x[0,0])+y[0,0];
}else if(i==n){
res=(z[n-2,0]*(x[n-1,0]-x[n-2,0])+(y[n-1,0]-y[n-2,0])/(x[n-1,0]-x[n-2,0])
)*(xx-x[n-1,0])+y[n-1,0];
}else{
res=( ( (z[i,0]-z[i-1,0])/(x[i,0]-x[i-1,0])
*(xx-x[i-1,0])+3*z[i-1,0]
)*(xx-x[i-1,0])+(y[i,0]-y[i-1,0])/(x[i,0]-x[i-1,0])
-(2*z[i-1,0]+z[i,0])*(x[i,0]-x[i-1,0])
)*(xx-x[i-1,0])+y[i-1,0];
}
return res;
}
}
]]>
</DnaLibrary>
これにより, 最初に示したような補間結果となる.
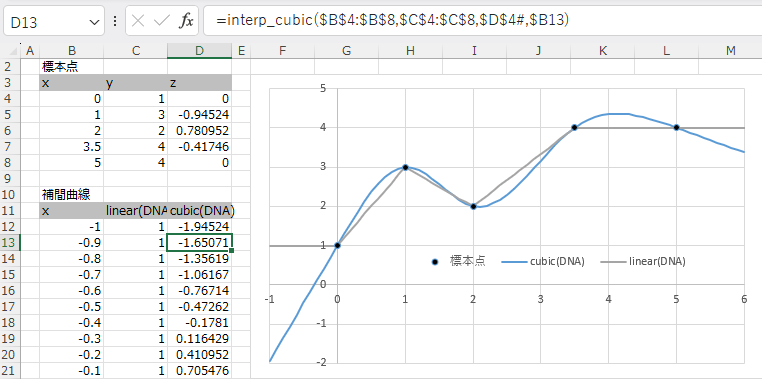
(比較のため, 同時に線形補間も図示している. 線形補間についてはこちらを参照.)







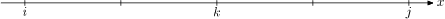

Discussion