はじめに
学習の忘備録として書いており,なんとなく理解したい初心者向けです.
完全な嘘があればご教授ください.
CAM(Class Activation Mapping)[1]
ざっくり説明すると,CNN がどこを見て判断したのかを可視化する手法です.後述するモデル制約があるため,Grad-CAM に一般化されています.
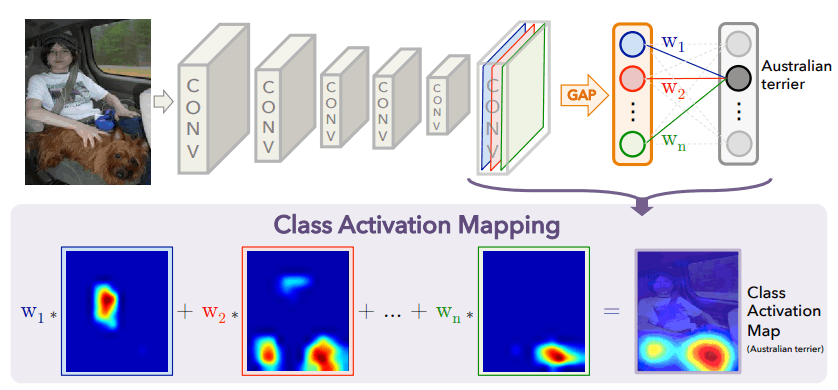
[1]より引用
CAMの意味するところは複雑ではないので,以下の数式と上図を照らし合わせて理解します.
S_c = \sum_{k} w_c^k (\frac{1}{Z} \sum_{i,j} A^k_{ij}) \\
= \frac{1}{Z} \sum_{k} \sum_{i,j} w_c^k A^k_{ij} \\
= \frac{1}{Z} \sum_{i,j} \sum_{k} w_c^k A^k_{ij} \\
= \frac{1}{Z} \sum_{i,j} L_{CAM}^c (i,j)
S_c はクラス c の出力で,図でいうところの Australian terrier です.A^k_{ij} は,上図の色付けされた k 番目の特徴マップのピクセル位置 (i,j) を示しています.また,Z は特徴マップの全ピクセル数となっています.つまり,数式の 1 行目のカッコ内は k 番目の特徴マップの Global Average Pooling(GAP) を示しており,全結合層への入力と対応していることがわかります.よって,1 行目は最終特徴マップから出力を表しています.2 行目は自明なレベルでの積の順序交換をしており,3 行目の \sum は互いに依存していないので入れ替え可能です.4 行目で L_{CAM}^c (i,j) = \sum_{k} w_c^k A^k_{ij} と定義することで完成です.
ここまで来ると式変形の意味がようやく見えてきます.つまり,S_c を (i,j) の和として表現し直すことで,ピクセル位置 (i,j) によって S_c への寄与が変わる(=どの位置が出力にとって重要なのかがわかる) ように解釈できるようになったということです.
上式から,「conv層 \Rightarrow GAP \Rightarrow FC層 \Rightarrow 出力」の流れが CAM を適用するためのモデル制約であることもわかります.
Grad-CAM[2]
前述したモデル制約について,一体どこが制約なのかと感じる人がいるかもしれません.クラス分類タスクモデルはこのアーキテクチャ構成が多いですが,物体検出などの他のタスクではこの構成とは限りません.以下の図が非常にわかりやすいので示しておきます.(Guided Grad-CAM部分はいったん無視してください)
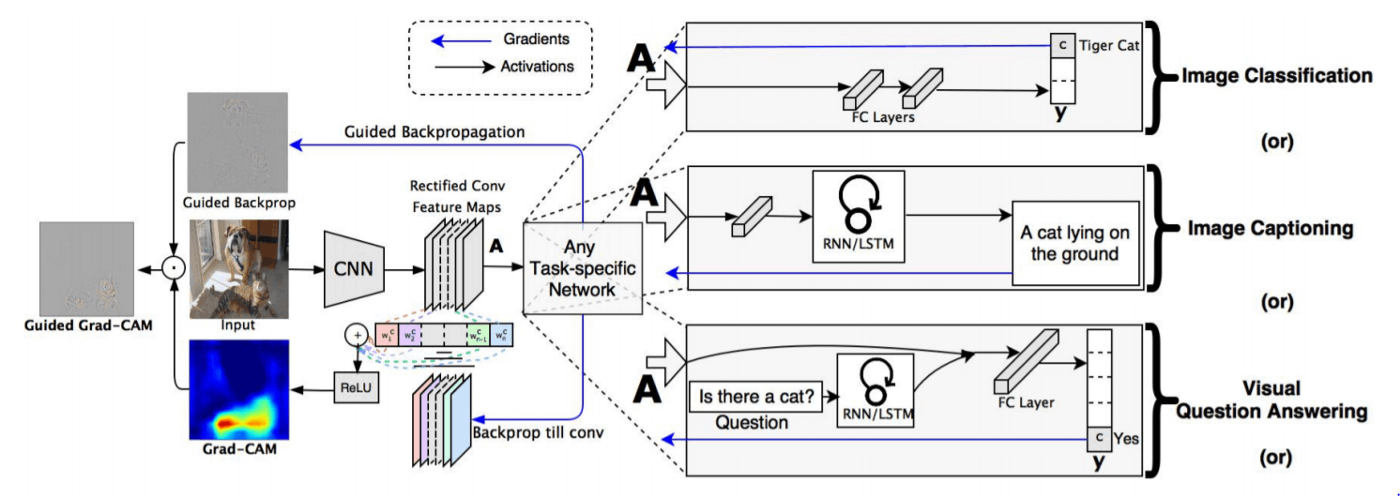
[2]より引用
上図の Any Task-specific Network(中央部)を見ると,conv 層の後の流れが多様であることがわかります.実は Grad-CAM では CAM の説明時の数式内で示した w_c^k の代わりになるものを用いて,モデル制約を解消しています.以下に Grad-CAM の式を示します.CAM 部分で示した L_{CAM}^c(i,j) に置き換えて考えてください.
L_{\mathrm{Grad-CAM}}^c(i,j) = \mathrm{ReLU}(\sum_{k} \alpha_c^k A^k_{ij})
CAM と異なる点は以下の 2 点です:
-
w_c^k から \alpha_c^k への代替
-
\mathrm{ReLU} の登場
順に考えていきます.
まず,1について見ていきます.\alpha_c^k は以下の式で表されます.
\alpha_c^k = \frac{1}{Z} \sum_{i,j} \frac {\partial S_c}{\partial A^k_{ij}}
混乱しますね.しかし,個々の役割を意識するとなんとなく理にかなっていそうなことがわかります.そもそも w_c^k は,「出力 S_c に対する k 番目特徴マップの重要性」を表していました.では,\alpha_c^k も「出力 S_c に対する k 番目特徴マップの重要性」を表してほしいです.上式を要素ごとに分解してみると,\frac{\partial S_c}{\partial A^k_{ij}} は「k 番目の特徴マップの位置 (i,j) の値を 1 増やすとどれだけ S_c が変化するか」を示しています.k 番目の特徴マップすべての位置に対して平均を取っているので,「k 番目の特徴マップのどこかの位置の値を 1 増やすと平均してどの程度出力 S_c が変化するか」を表しており,「k 番目の特徴マップの重要性」を示すと解釈できそうです.w_c^k と異なり特徴マップ A_k^c から出力までの道筋を制限していないので,逆伝播により微分値が求まれば適用できるという寸法です.
続いて,2 についてですが,\mathrm{ReLU} をとるということは,負の出力には興味がないということを意味します.つまり,L_{\mathrm{Grad-CAM}}^c(i,j) が負であれば,注目しているクラスの出力値を低下させることにつながり,今注目しているクラス出力には寄与しないため,排除していると考えることができます.
おわりに
今回は,直感的な CAM と Grad-CAM の説明をしてみました.Grad-CAM の元論文[2]をよむと,より丁寧な導出と説明がなされていますので興味を持たれた方は参照してみてください.実は Grad-CAM にはいろいろと問題点があることが指摘され,今もなお賢い人たちによって多くの改良手法が提案されています.
本記事が興味の足掛かりにでもなればと思っております.
[1]https://arxiv.org/abs/1512.04150
[2]https://arxiv.org/abs/1610.02391


Discussion