関節点、橋とlowlinkの行間

はじめに

関節点とは、無向グラフの頂点であって削除すると連結成分の数が増えるもののことです。
橋とは、無向グラフの辺であって削除すると連結成分の数が増えるもののことです。
lowlinkとは、関節点や橋を線形時間で求められる手法です。

これらについての解説は沢山ありますが、読んだ時に言葉ではいまいちピンと来なかった部分があったのでこの記事では図を使って行間を埋めることを目的とします。

解説や実装例そのものは良いものが沢山あるのでここでは扱いません。

良いものの例

• アルゴリズムロジック
• Luzhiled's memo

関節点、橋の判定方法

lowlinkでは各連結成分について、適当な根を決めたうえ(本当に何でもいい)それぞれの頂点について以下2つの値を求めます。
ord$[i]$: 頂点$i$のDFS行きがけ順(pre-order)
low$[i]$: 頂点$i$から葉方向の辺を0回以上、後退辺を高々1回使って到達できる頂点のordの最小値

これらを用いて、

• 頂点$i$が根のとき、$i$に子が2つ以上あれば$i$は関節点
• 頂点$i$が根でないとき、$i$に ord$[i]\leq$ low$[j]$ になるような子$j$が存在すれば$i$は関節点
• DFS木上で頂点$i$と$i$の子$j$を結ぶ辺$(i,j)$が ord$[i]<$ low$[j]$ なら$(i,j)$は橋
• (DFS木上にない辺は自明に橋ではない)

と判定することができます。

ピンと来なかった点1: 判定式の微妙な違い

判定式が関節点では$\leq$、橋では$<$になり、その理由を日本語で説明してくれる記事は沢山ありましたが脳内で絵が描けなくてピンと来ませんでした。
なので補足するためにミニマムな絵を描きます。

関節点の判定

まず、左の連結グラフからlowlinkによって右のようなDFS木ができたとします。

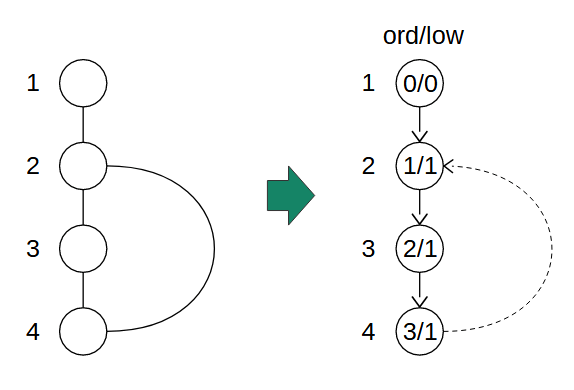
①このとき頂点$2$は関節点で、ord$[2]=1$, low$[3] = 1$ なので確かにord$[2]\leq$ low$[3]$ を満たします。

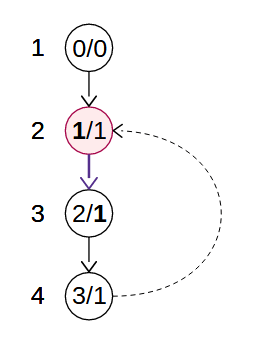
②また、頂点$3$は関節点ではなく、ord$[3]=2$, low$[4]=1$ なので確かにlowが$2$以下の頂点は存在しません。

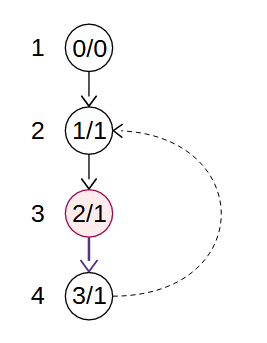
橋の判定

③次に、辺$(1,2)$は橋で、ord$[1]=0,$ low$[2]=1$ なので確かにord$[1]<$ low$[2]$を満たします。

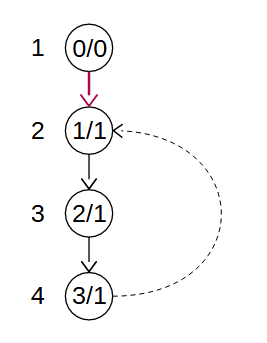
④また、辺$(2,3)$は橋ではなく、ord$[2]=1,$ low$[3]=1$ なので確かにord$[2]<$ low$[3]$を満たしません。

等号の有無

ここで、①と④は同じ辺を判定に使っていますが等号の有無によって判定結果が変わっています。
絵をグっと睨むと頂点$3$以下から頂点$2$に戻ってこれる辺があればord$[2]=$ low$[3]$ になりますが、頂点$2$を消してしまえばそんな辺もろとも消えてしまうので連結性を保てないことが分かります。
また、同様にそのような辺$(4,2)$は辺$(2,3)$を消しても無事なので$2\rightarrow4\rightarrow3$と辿れることが分かります。

これで私は納得しました。

ピンと来なかった点2: 根の判定条件

頂点$i$が根のとき、$i$に子が2つ以上あれば$i$は関節点
と見て、いやいや部分木同士が後退辺で繋がってたら$i$は関節点になれないのでは？　と思いました。
例えばこんな絵です。頂点$1$は根であり子を2つ持っていますが、関節点ではありません。

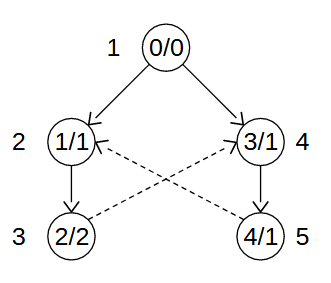
絵をじっと見ます。

…これはDFS木でしょうか。

違います。
元のグラフをDFSすると頂点$3$で引き返すはずはなく頂点$4$へ移動して探索を続け、最終的に以下のようなDFS木ができあがるはずです。

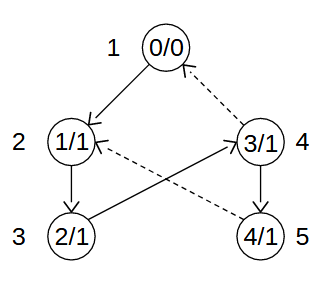
このDFS木上で頂点$1$の子は1つで、確かに頂点$1$は関節点ではありません。

これで私は納得しました。

以上