再帰関数、DFS(深さ優先探索：depth-first search)とは？

再帰関数とは？

再帰関数とは、自身の中で自分自身を呼び出す関数のことです。
同じ処理を繰り返す必要がある場合に使われ、プログラムを簡潔に書くことができます。
「再帰」という言葉は「繰り返し帰る」という意味で、プログラムでは、関数が呼び出しを繰り返し、最終的に終了条件（基底条件）に到達して処理を終えます。

DFS(深さ優先探索)とは？

DFS（Depth-First Search）は、木構造やグラフ構造を探索するアルゴリズムの一つです。
「深く進む」という動作を繰り返し、目的の要素を探します。探索が行き止まりになった場合には、探索を一旦戻り（バックトラック）、他の経路を探索します。

問題

1（島）と0（海）の地図を表すm×nの2次元2進格子が与えられたとき、
1の集まりを見つけてその数を返すプログラムを作成する問題です。

https://leetcode.com/problems/number-of-islands/description/
LeetCode-200. Number of Islands

考え方

1. 2次元配列を順番に探索を行い1を見つける。
2. 1を見つけると探索済みとして0にして、その場所を基準に全方位を探索します。
3. 1が見つからなくなるまで2.を再帰的に探索を続けます。
4. 探索が終了すると島一つ分が0となり、島の数をカウントします。
5. 1.を続きから探索を行い、2次元配列の最後まで探索を行います。

以下に考え方のgifを示します。

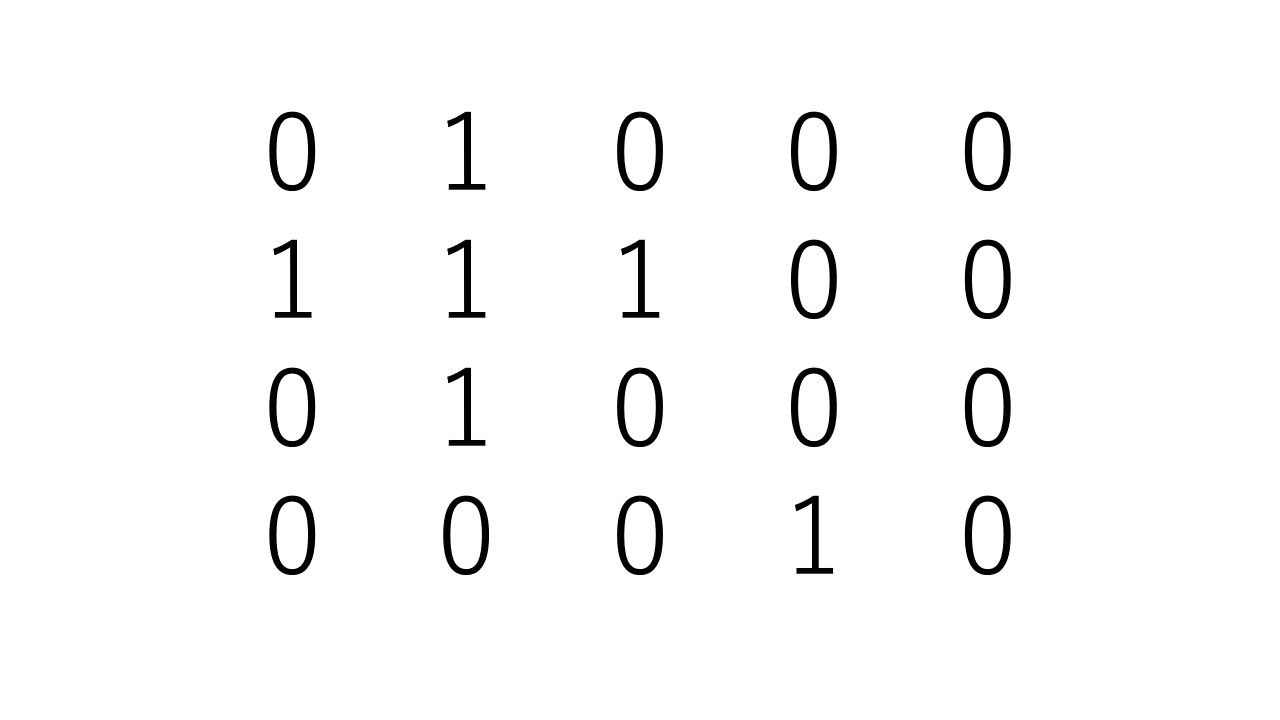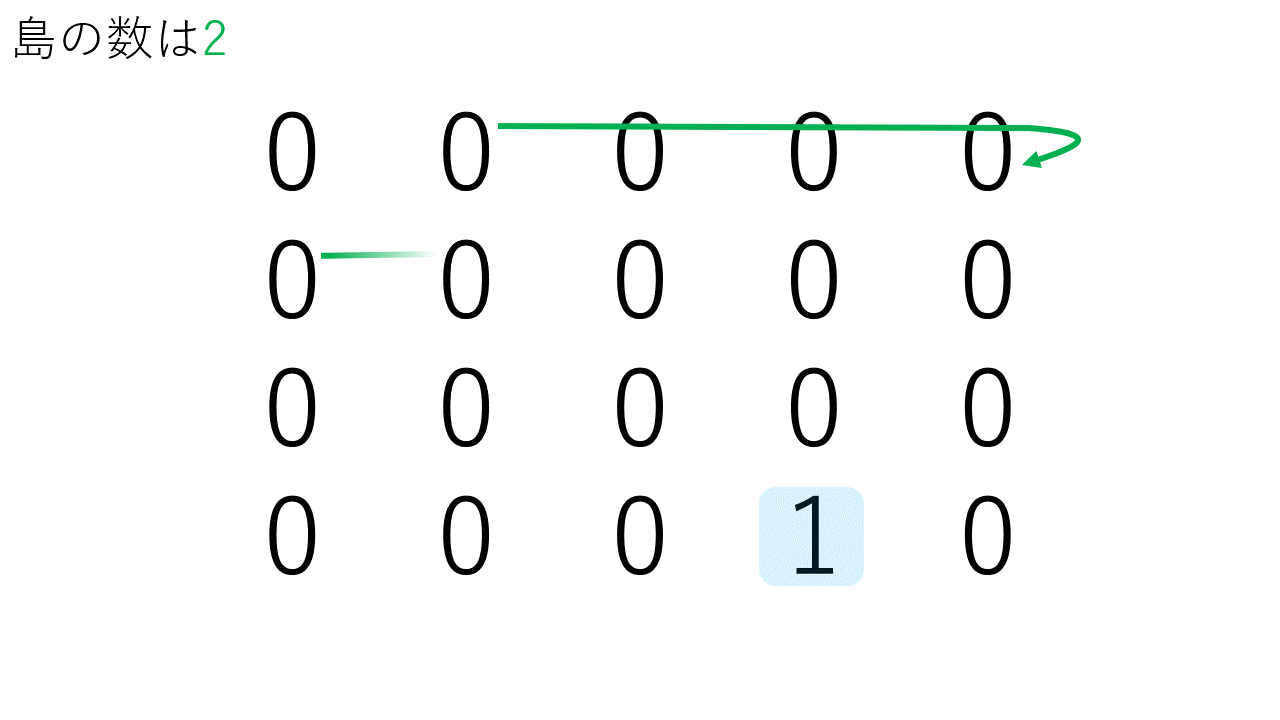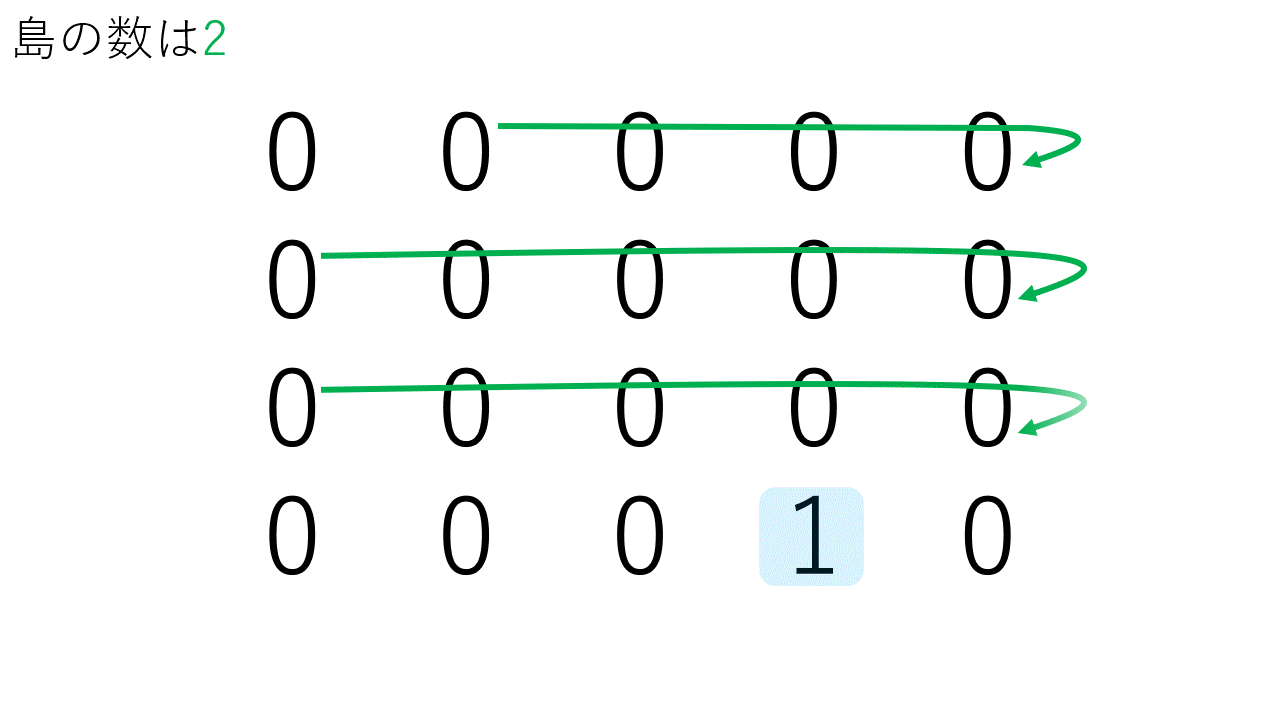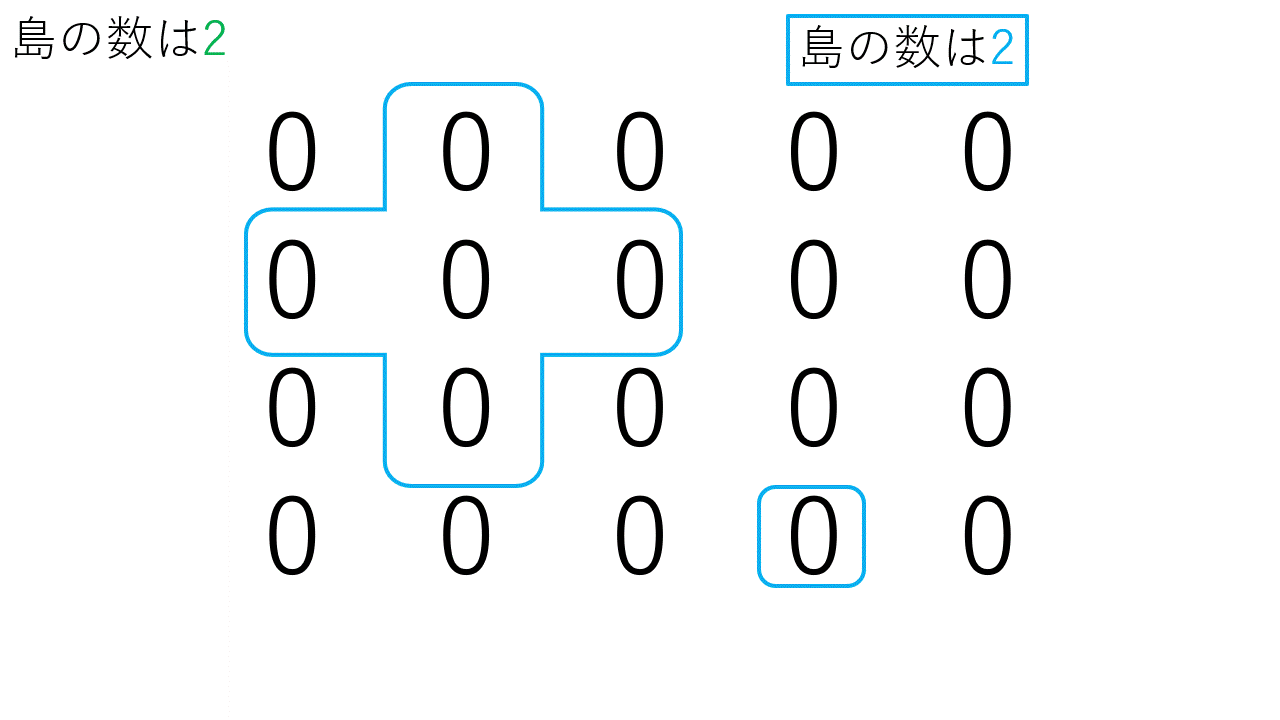
コード

• dfs関数
  -1. 配列の範囲外、探索先が0の場合は早期returnします。
  -2. 1の場合は0にします。
  -3. 再帰的に探索を行い、1(島一つ分)を0にします。

• numIslands
  -1. 2次元配列を全探索を行い、1を見つけると島の数としてカウントします。
  -2. dfs関数を呼び出し、1(島)の探索を始めます。

以下にコードを示します。

ソースコード.cpp

#include <iostream>
#include <vector>

class Solution {
private:
    void dfs(std::vector<std::vector<char>>& grid, int col, int row)
    {
        if (col < 0 || row < 0 || grid.size() <= col || grid[col].size() <= row || grid[col][row] == '0')
            return;

        grid[col][row] = '0';

        dfs(grid, col - 1, row); // 上
        dfs(grid, col, row + 1); // 右
        dfs(grid, col + 1, row); // 下
        dfs(grid, col, row - 1); // 左
    }

public:
    int numIslands(std::vector<std::vector<char>>& grid)
    {
        int landsCount = 0;
        for (int c = 0; c < grid.size(); c++)
        {
            for (int r = 0; r < grid[c].size(); r++)
            {
                if (grid[c][r] == '1')
                {
                    landsCount++;
                    dfs(grid, c, r);
                }
            }
        }
        return landsCount;
    }
};

int main()
{
    Solution s;
    std::vector<std::vector<char>> a;

    a = {
        {'0','1','0','0','0'},
        {'1','1','1','0','0'},
        {'0','1','0','0','0'},
        {'0','0','0','1','0'},
    };
    std::cout << s.numIslands(a) << std::endl;

    return 0;
}

以下に実行結果を示します。

2

コード解説

以下に探索の様子をgifで示します。

再帰関数のメリット・デメリット

• 再帰関数のメリット

  1. 複雑な問題を簡単に解ける
  2. コードが簡潔で処理内容が分かりやすい。
     ループや手動でのスタック管理を省略できるため、コードがシンプルで読みやすくなります。

• 再帰関数のデメリット

  1. スタックオーバーフローのリスク
     探索範囲が非常に深い場合、関数呼び出しが多くなりスタックメモリが不足することでプログラムがクラッシュします。
  2. パフォーマンスの低下
     再帰呼び出しでは関数のオーバーヘッド（呼び出しごとのメモリ割り当て）が発生するため、反復処理（ループ）と比べて遅くなる場合があります。

https://www.momoyama-usagi.com/entry/info-algo-saiki#i-4:~:text=*3。-,３．再帰を用いるメリットとデメリット,-メリット　見栄え
うさぎでもわかる再帰関数のいろは-３．再帰を用いるメリットとデメリット

再帰関数を使わないコード

再帰関数を使わない場合はループの数が増えて、スタックも用意する必要がある。
以下に再帰関数を使わない例を示します。(コードの生成にchatGPTを使用しています。)

ソースコード.cpp

#include <iostream>
#include <vector>
#include <stack>

class Solution {
public:
    int numIslands(std::vector<std::vector<char>>& grid)
    {
        if (grid.empty() || grid[0].empty()) return 0;  // 空のグリッド処理

        int landsCount = 0;
        int rows = grid.size();
        int cols = grid[0].size();

        // 4方向移動用のベクトル (上下左右)
        std::vector<std::pair<int, int>> directions = { {1, 0}, {0, 1}, {-1, 0}, {0, -1} };

        for (int c = 0; c < rows; c++) {
            for (int r = 0; r < cols; r++) {
                if (grid[c][r] == '1') {  // 新しい島を発見
                    landsCount++;

                    // スタックを使った反復的DFS
                    std::stack<std::pair<int, int>> stack;
                    stack.push({ c, r });
                    grid[c][r] = '0';  // 訪問済みとしてマーク

                    while (!stack.empty()) {
                        std::pair<int, int> current = stack.top();
                        stack.pop();
                        int curC = current.first;
                        int curR = current.second;

                        for (auto dir : directions) {
                            int newC = curC + dir.first;
                            int newR = curR + dir.second;

                            // 境界条件と未訪問チェック
                            if (newC >= 0 && newC < rows && newR >= 0 && newR < cols && grid[newC][newR] == '1') {
                                stack.push({ newC, newR });
                                grid[newC][newR] = '0';  // 訪問済みとしてマーク
                            }
                        }
                    }
                }
            }
        }

        return landsCount;
    }
};

int main()
{
    Solution s;
    std::vector<std::vector<char>> a = {
        {'0','1','0','0','0'},
        {'1','1','1','0','0'},
        {'0','1','0','0','0'},
        {'0','0','0','1','0'},
    };
    std::cout << s.numIslands(a) << std::endl;  // 出力: 2

    return 0;
}

おまけ

Pythonは勉強中です。(chatGPTも併用しています)

200. Number of Islands.ipynb

class Solution:
    def dfs(self, grid, col, row):
        if col < 0 or row < 0 or col >= len(grid) or row >= len(grid[0]) or grid[col][row] == '0':
            return

        grid[col][row] = '0'

        self.dfs(grid, col - 1, row)  # 上
        self.dfs(grid, col, row + 1)  # 右
        self.dfs(grid, col + 1, row)  # 下
        self.dfs(grid, col, row - 1)  # 左

    def numIslands(self, grid):
        lands_count = 0
        for col in range(len(grid)):
            for row in range(len(grid[0])):
                if grid[col][row] == '1':
                    lands_count += 1
                    self.dfs(grid, col, row)
        return lands_count


if __name__ == "__main__":
    s = Solution()
    a = [
        ['0', '1', '0', '0', '0'],
        ['1', '1', '1', '0', '0'],
        ['0', '1', '0', '0', '0'],
        ['0', '0', '0', '1', '0']
    ]
    print(s.numIslands(a))