Flow Q-Learning

本記事では、Flow Q-Learning の概要とその技術的特徴、そして実験結果について解説します。

元論文
Flow Q-Learning

公式のサイト
https://seohong.me/projects/fql/

公式のgithub
https://github.com/seohongpark/fql

概要

Flow Q-Learning (FQL) は、Flow Policy を蒸留して One step Policy を作ることで、複数ステップのノイズ除去を回避し高速な推論を実現しています。また、蒸留モデルを用いた Q 学習で安定性を向上させ、D4RL や OGBench のタスクで既存手法を上回る性能を示しました。

先行研究との違いは

Diffusion Policy:
Diffusion Policyはロボティクスや制御の分野で注目を集める一方で、学習の不安定さや多くのdenoisingステップが必要という課題があります。
そこでFlow Matching を用いることで、学習の安定性が向上します。また、蒸留により 1 step の denoising が可能となり、Diffusion Policy に比べ推論速度が大幅に改善されます。

TODO
Consistency-AC
SRPO

技術のキモは？

FQLの最終的な損失関数は以下の通りです。

$$L = L_{flow} + L_{actor-critic} + L_{distill}$$

ここで、Flow Policy のパラメータを $\mu_{\theta}$、蒸留モデルのパラメータを $\mu_{\omega}$ とします。
本手法では、Q学習の安定性を向上させるため、actor critic の更新は蒸留モデル $\mu_{\omega}$ を用いて行います。

学習は以下の図のように表されます。

• flow policyで$\mu_{\theta}$を学習する（図の上）
• distillでone stepのpolicyの$\mu_{\omega}$を学習する（図の下）
• Q学習で、報酬が高い行動分布のみを学習できる（図の上から下への矢印）
  

Flow Matching

まず、Flow Matching を用いて Policy を学習します。本論文では Rectified flow に基づき、初期分布 $x_0$ からターゲット分布 $x_1$ へは直線（straight path）で繋がれていると仮定します。任意の時刻 $t$ における状態 $x_t$ は $x_0$ と $x_1$ の内分点として、次にように書けます。

$$x_t = t*x_1 + (1-t)*x_0$$

この直線上で、$x_t$ から $x_1$ までの勾配$\dfrac{dx}{dt}$は次ように書けます。

$$\dfrac{dx}{dt} = x_1 - x_0$$

これにより、モデル $\mu_{\theta}$ は以下の損失関数を最小化することで学習されます。

$$\min_{\theta} \left\|\mu_{\theta}(t, x_t) - (x_1 - x_0)\right\|^2$$

学習済みのモデル $\mu_{\theta}$ を用いて、Diffusion Policy と同様に、複数回のノイズ除去ステップを実行し、以下の更新式で状態を生成します。

$$x_t = x_{t-1} - \dfrac{\mu_{\theta}(t,x_t)}{T}$$

蒸留

Flow Policy は複数のノイズ除去ステップを必要とするため計算時間がかかり、またアクションが定まりにくいため Q 学習時の Q 値が不安定になりやすいという課題があります。これを解決するため、Flow Policy から蒸留するモデル $\mu_{\omega}$ を学習し、次の損失関数

$$\min_{\omega} \left\|\mu_{\omega} - \mu_{\theta}\right\|^2$$

Offline RL

actor criticの式は次のように書ける
critic lossはQ学習から次のように書ける。
このときのnext action: $a'$はdistill policyから計算される。

$$L_{critic} = \mathbb{E}_{a' \sim \pi_{\mu_{\omega}}} \left[ r + \gamma Q(s', a') - Q(s,a) \right]$$

actor clossは次のように書ける

$$L_{actor} = \mathbb{E}_{a \sim \pi_{\mu_{\omega}}} \left[-Q(s, a)\right]$$

Q値を最大にするような行動aを最適化する際、aは蒸留モデル$\mu_{\omega}$によって生成されます。このアプローチにより、蒸留モデルを用いたQ学習で安定性が向上することが期待されます。

結果

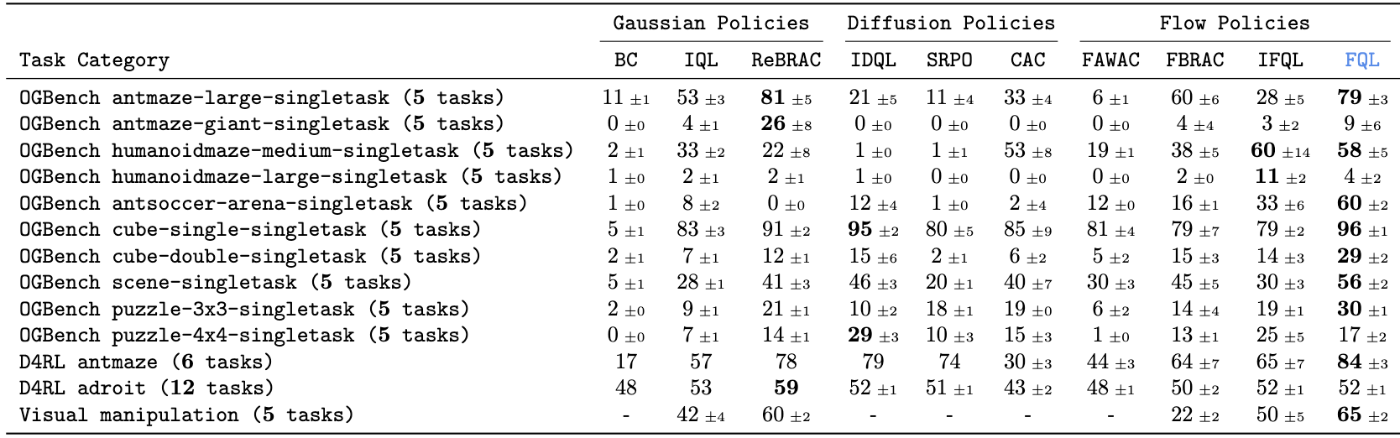
シミュレータ上で実施した多様な実験により、FQL の有効性が確認されました。

結果として、FQL は BC や Diffusion Policy などと比較して最も高い性能を示しました。図からも、Gaussian Policies や Diffusion Policies に比べ、Flow Policies のほうが全体的に精度が高いことが分かります。また、Offline RL 手法である BRAC と Flow Policy を組み合わせた FBRAC よりも、FQL のほうが精度が向上しており、蒸留手法が大きな役割を果たしていると考えられます。

※ 著者によると、蒸留損失の係数 $\alpha$ が性能に大きな影響を与えるとのことです。

まとめ

Flow Q-Learning は、Flow Matching と蒸留技術を組み合わせた新しい手法であり、Offline RL の学習不安定性を大幅に改善しました。さらに、Diffusion Policy と比べ、Flow Matching はシンプルな数式で表現できるにも関わらず、十分な精度を確保しており、今後ますます注目されると考えられます。