ステータス

統計学自体はちょっとはやった(準1級はもっている)
が応用はあまり経験がない
ベイズのことは定理と推定の概要をほんのりと理解している程度。ほぼ初対面。

目標

ベイズ推定とMCMCについて仕組みを理解し、説明できるようになる
実務への応用の仕方をイメージできるところまで

参考書

いったん手元にあるこれとか
https://www.amazon.co.jp/dp/B07919W1YX

こうやってく

ベイズと頻度の違い
~~計算(実装)のしかた~~
~~MCMCの理屈と利用方法~~
実務に使うならどういうときか考えてみる

akitokoga

ちがいまとめ

大きな違いは「パラメータをモデル化するかどうか」にありそう。なので確率や信用区間が直接出せる。けどモデル選択をミスると見当外れになるので、自由度が高いことが諸刃になることもありそう。

どちらかというと数理モデル化っぽく、古典統計とは全然異なるものという認識の方がいいかもしれない。

頻度論では真のパラメータがあり、観測されるデータは確率変数。
ベイズではパラメータは変化するが、観測のたびに得られるデータは変化しないと考える。
頻度論では「偶然と考えたときにこのデータが実現する確率」を求め、一定(p値)以下であれば偶然でないと判断する
ベイズは仮定したパラメータに基づく分布から直接確率を求める。
一般にどちらがいいというわけではないが、ベイズを選ぶメリットとしては
- 事前に得られた情報を使って更新していける
- シミュレーションに当てはめて推定できる

参考

https://ai-trend.jp/basic-study/bayes/basic-2/

akitokoga

計算の仕方編

簡単なのは共役事前分布を使って推定する方法。

ざっくりだと、
確率 → 二項分布 → ベータ分布
個数 → ポアソン → ガンマ分布
連続量 → 正規分布 → 正規分布

MAP推定

頻度論でいう最尤推定となるもの。事後確率を最大にする区間。

HPD

最高事後密度信用区間。最大の密度( = 最頻値)周辺の信用区間。

カーネル密度推定

あとで

信用区間

数理モデルに近い分「95%の確率でここに収まる」という範囲がダイレクトに出せる。古典統計は「パラメータがこの範囲にある確率は95%」であり、明確に異なる。（が、出てくる数値はけっこう近い）

変数変換

Beta分布とか、片裾が長かったり途切れのあるモデルだと平均値とかのパラメータに意味がなくなる。
$\arcsin \sqrt{x}$ 変換するといい具合に等裾っぽくなるテクニックがある。
本では目盛の幅を変えると書いてあったけど、単純に変数変換したらいいし、それよりかはパラメータに変換をかける方がより当てはまりがよいのでは、と思った

階層モデル

あとで

akitokoga

ベイズ推定をやってみる

まずはベイズ更新から

1. 自社サービスのタブレット対応の検討

設定する状況

タブレット対応するか検討するため、ユーザーのタブレット利用率を推定したい
総務省が調査した結果は存在するが、ユーザーに関しては利用率が異なるかもしれない
ので、調査の結果を参考にしつつ、アンケート結果を用いてどれくらいになるか推定したい

数値の設定

総務省の調査によれば、単身世帯は25.3%,2人以上世帯は43.8%。
N=8,400、三段抽出法とのことなので、それぞれのNを4,200ずつと考える。
50名(二人以上世帯)のユーザーヒアリング(架空)の結果25人がタブレットを使っていたことがわかった。

事前分布

二人以上世帯のユーザーの利用率より、利用していると回答した人は1,839人。

事前分布 $\propto ~Bin(4200,0.438) \propto p^{1839}(1-p)^{2360}$

尤度

尤度はヒアリング結果より、

尤度 $\propto p^{25}(1-p)^{25}$

事後分布

事後分布 $\propto p^{1839}(1-p)^{2360} * p^{25}(1-p)^{25} = p^{1864}(1-p)^{2385}$

推定

事後分布を微分すると $p^{1863}(1-p)^{2384}{1864(1-p)-2385p}$ 。 $p\neq 0,1$ より、 $p=\frac{1864}{4249} = 0.43869$

結果

二人以上世帯に関しては事前に得ていた確率0.438が0.4387に変化した。ヒアリング結果から考えるとずいぶんと総務省の調査結果に寄ってしまっている。これはNが4200:50とかなり差があることが影響している。

これを補正するためのには、事前分布をどれくらい重視するかというパラメータを用意して加重平均みたいにする方法がありそうだけど、パラメータを恣意的に設定しやすいので今回は触れずにこれでおしまいにする。

akitokoga

ベイズ推定をやってみる②

クラッシュするユーザー数を推定する

段階公開の過程で得られるクラッシュ状況から、全体公開した際のクラッシュ数予測を推定したい
単純に公開率の逆数をかけるのとどれくらい異なるのか比較してみる

設定

1%公開時点でクラッシュが1件でた
5%公開時点では累計クラッシュが7件だった

モデル化する

方針

カウントデータなのでポアソン分布に当てはめる
ポアソン分布は「単位時間あたりの発生回数」を表現するけど、公開状況によってユーザー数が変化するので単位を揃えないといけない
今回は求めたいクラッシュ数 $\lambda$ に公開率をかけることで表現してみる

1回目の観測

参考書籍によると、ポアソン分布の無情報事前分布には $x^{-1/2}$ を使うのがよいらしいので、素直に従ってみる。(フィッシャー情報量をウニャウニャすると出せる)

ポアソン分布： $p(y|x) = \frac{x^{y}e^{-x}}{y!}$

事前分布： $x^{-1/2}$
尤度：ポアソン分布に $y=1,x=0.01\lambda$ を代入する
事後分布 $\propto x^{-1/2} * (0.01\lambda)e^{-0.01\lambda} = (0.01\lambda)^{1/2}e^{-0.01\lambda} \propto Gamma(\frac{3}{2},0.01)$

この確率密度関数を図示すると以下のようになり、50~100あたりになる可能性が高そうな感じがする。

curve(dgamma(x,1.5,0.01),0,500)

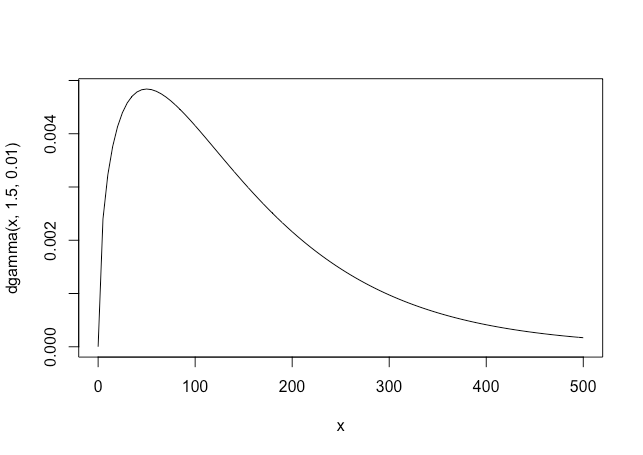
gamma(1.5,0.01)のグラフ

統計量については以下のようになる
95%信用区間： $[10.78976,467.42018]$
中央値： $118.29869$
最頻値： $50$
期待値： $150$

> qgamma(c(0.025,0.5,0.975),3/2,0.01)
[1]  10.78976 118.29869 467.42018

10~467までの間と言われても正直全然参考にならないけど、直感的に100前後になりそうという印象よりは詳しい情報が得られている。
裾が長い分期待値としては大きくなってしまうものの、最頻値50は救いのある情報っぽい

ちなみに、この時点で得られる情報からクラッシュ数が100以上になる確率を推定してみると、57%ほどになった。モデル化するとこういうのが一発で出るのがよいな(普通に積分した方が正確だけど)

> r = rgamma(100000,3/2,0.01)
> mean(r > 100)
[1] 0.57299

更新してみる

上の段階で得られた情報を事前分布にして、5%公開時で7件の情報を加えてベイズ更新してみる。
5%公開時の情報では1%公開の情報が混じっているので除くと「追加で4%公開した時に6件のクラッシュが発生」とみることができる。(無記憶性があるからできる)

事前分布： $Gamma(\frac{3}{2},0.01)$
尤度： $(0.04\lambda)^6*e^{-6}$
事後分布 $\lambda^{13/2}e^{-0.05\lambda} * 0.01^{1/2} * 0.04^6 \propto Gamma(\frac{15}{2},0.05)$

これを図示してみると以下のようになり、さっきよりも明らかに分布が右に移動し、クラッシュ発生が増えていることが反映されている

curve(dgamma(x,7.5,0.05),0,500)

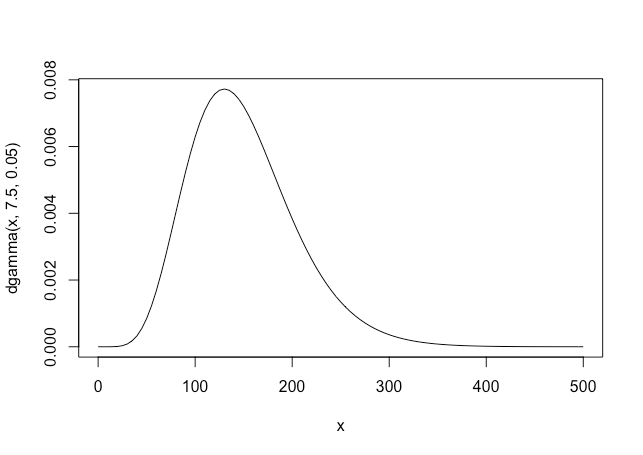
gamma(7.5,0.05)

これの統計量を求めてみると、両方の裾が縮まり、最頻値が50→130と大きく更新されていることがわかります。期待値が変わらなかったのはたまたま。

95%信用区間： $[62.62138,274.88393]$
中央値： $143.38860$
最頻値： $130$
期待値： $150$

> qgamma(c(0.025,0.5,0.975),7.5,0.05)
[1]  62.62138 143.38860 274.88393

この分布の状態でクラッシュが100以上になる確率を推定してみると、82%になった。早めに修正した方が良さそうですね。

> r = rgamma(100000,7.5,0.05)
> mean(r>100)
[1] 0.82114

疑問

そもそも推定するパラメータに $0.01\lambda$ なんてしてよいんだろうか