👾

【読切】めっためたにメタ学習

に公開
AI
メタ学習
論文要約
LLM
idea

背景

以前のLLMプロンプトエンジニアリングの記事で, Meta Promptingを紹介した. これは, 大規模言語モデル(LLM)をさまざまなタスクに適応させる, さまざまなタスクでの回答精度を向上させるようなプロンプト（ベクトル）を自動で生成するSoft Promptingの一種である.

なかでも, Meta Promptingは, メタ学習の枠組みであるMAML (Model-Agnotsic Meta-Learning) を使用し, さまざまなタスクに適応できるプロンプト（ベクトル）を安定的かつ効率的に生成する手法である.

ただ, 肝心のメタ学習が何ものなのか？ということをよくわかっておらず, 改めて調べ直すことにした.

そこで, 本記事ではメタ学習に関する以下のサーベイ論文をベースに, メタ学習とは何か？という話から, どんなドメインで使われるの？というアプリケーションの話までまとめて整理したいと思う（長くなること必至なので気をつけてください😇)

https://arxiv.org/abs/2004.05439

メタ学習とは

前提として, 「メタ学習とはそもそもなんですか？なにを目的とした技術ですか？」 ということを説明しておく.

論文にも書いてあるが, メタ学習とは, 学び方を学ぶ (Learning to learn)手法 である.

https://gen-ai-media.guga.or.jp/glossary/meta-learning/

話を戻すと, メタ学習も, タスク特化の学び方をするのではなく, さまざまなタスクに適用できるような汎用的な学びのプロセス自体を学ぶ（改善）していくことに焦点を当てている.

その背景には, これまでの機械学習がタスク特化に取り組んでいたことにおけるさまざまな課題が意識されている.

従来の機械学習は, 特定のタスクに向けて0から学習をし直すというアプローチであった. しかも, この方法が適切に機能するには, 特定のタスクにおける入力と出力（＋ラベル）のデータセットが十分になければいけなかった.

しかし, 分野にとっては十分なデータを取得されない場合もあるし, そもそもデータが手に入っていても, 時間のかかる学習コストが解消されないことには,特定のドメインでの機械学習の適用は難しい（例：医療や自然言語）

そうした課題に対処するために, 効率的かつ少数データでも機能する学習論を提案したものがメタ学習である.

さて, 一旦メタ学習とはなにか？というものを整理しよう.

メタ学習の定式化

さきのセクションで, 「メタ学習のやりたいこと」を説明したので, 本セクションでは, 「「メタ学習のやりたいこと」をどう実現しているのか？」 について説明する.

従来型学習法(Base-Learning)

まずは従来型学習法(Base-Learning, とよぶ) の考え方を式に表してみる.

いま, あるドメイン（タスク）のために収集されたデータセット D = \{(x_1, y_1), \cdots, (x_N, y_N)\}　があるとし, このデータセットの入出力関係を学習するモデル, あるいは予測するモデルを構築したいとする. (ここで,画像タスクを考えると, インプットx_iは例えば画像であり, アウトプットy_iはラベルである)
つまり, \hat{y} = f_{\theta}(x)なる学習モデルfを学習したい. このとき, 学習モデルfを決めるパラメータ\thetaは次の損失関数の最小化問題を解くことで求められる.

\begin{align} \theta^{*} = \argmin_{\theta} L (D; \theta, w) \end{align}

ここで, Lはロス関数でである.そして, 式を見るとwが入っていることに気づいただろうか. このwは学習プロセス(how to learn）に関する設定項目で, 例えば, 学習モデルfを制御する\thetaのOptimizerの選択や, そもそもの学習モデルfの選択に関わる.

よくみかえるのは, wを含まない式だが, wを含めることで, この学習方法自体が, 学習方法に関するパラメータwによって条件づけられることを表している.

と, せっかく用意したwではあるが, 従来型学習法では, 事前に定義された学習アルゴリズムの選択を指し, 多くの場合固定されている.
そのため, 他のタスクに適用としても, すでに固定されているwでは, 他のタスクに適応できるような能力を持ち得ない.

なるほどー🧐, メタ学習はwの設定自体も学習の対象にいれること, 多様なタスクに適応できるような学習モデルを作ってしまおう! というものらしい.
まさに, 学び方自体を学ぶ, 仕組みということだ.

さて, メタ学習はあくまでも, 学び方自体を学ぶ仕組みに関する抽象的な概念である. つまりは, どう実現するかという定式化についてはいくつかの方法がある. 以降で, 論文で整理されている方法でわけ説明する.

Meta-Learning: Task-Distribution View

この分類方法では, さきの 「タスク間の一般化問題としてのメタ学習」 を定義する.
ここで, タスクTというものが定義される. これは, T = \{D, L\}のように, 特定のタスクのために収集されたデータセットDと, ロス関数Lのセットである.

すると, このメタ学習の目的は,以下の最小化問題を解wを見つけることである.

\begin{align} \min_{w} \mathbb{E}_{T \sim p(T)} \lbrack L(D;w) \rbrack \end{align}

さて, さきほどの式を解こうとする場合, p(T)からタスクデータセットTをサンプリングしたものを学習や検証に使用する. その場合, ２つの学習・検証の段階にわけている. Meta-Training stageとMeta-testing stageとにわかれる.

Meta-training stage

ここで, M個のsource tasksから作成されたデータセット\mathbb{D}_{source} = \{(D^{train}_{source}, D^{val}_{source}) \}^{M}_{i=1}を作る.

つまり, M個のタスク(例：犬/猫画像分類, 車/自転車画像分類)のそれぞれから, データをとって混ぜ合わせた新規のデータセット\mathbb{D}_{source}をつくる. このデータセットをもちいて以下の数式をとく.

\begin{align} w^{*} = \argmax_{w} \log{p(w | \mathbb{D}_{source})} \end{align}

ここで, メタ知識wに対し, 手元のデータセット\mathbb{D}_{source}で条件づけした\log{p(w | \mathbb{D}_{source})}を最大化している. つまり, 手元のデータセット\mathbb{D}_{source}に対し最も生起するwを探しているのだ.

このステージで, さまざまなタスクに通ずる, 学習方法に関する(暫定的な)メタ知識(meta-knowledge)が獲得される.

Meta-testing stage

つぎに, Q個のタスク(M個のタスクに含まれないもの,　つまり未知のタスク)それぞれから, データをとって混ぜ合わせた新規のデータセット\mathbb{D}_{target} = \{(D^{train}_{target}, D^{val}_{target}) \}^{Q}_{i=1}をつくる.

そして, 以下の式をタスクデータセット\mathbb{D}_{target}のそれぞれのタスクiごとに以下の最適化問題をとく.

\begin{align} \theta^{* (i)} = \argmax_{\theta} \log{p(\theta|w^{*}, D^{train (i)}_{target})} \end{align}

ここで最適化しているのが学習モデルfに関するパラメータ\thetaであることに注意すると,Meta-testing stageでは, 未知のタスクにでも有用なベースモデル（関数）を学習している.

比較

さて, 従来型学習法の式と比べると, 未知のタスクiに対して, 学習や予測する場合に, モデルのパラメータ\theta^{* (i)}はメタ知識w^{*}を活かせる構造になっていることがわかる.
これが, 学習方法を会得した(w^{*})上で行う効率的な学習モデルにつながっている.

この方法は, 初期パラの設定や, 全体学習モデル, 最適化戦略などにも応用がきく.

しかし, 弱点も指摘されている. 例えば, meta-underfittingやmeta-overfittingなどの従来的にいわれている未学習/過学習の話がタスクに限定して発生してしまう.

特に, meta-overfitting(おそらく, 特定タスクへの過学習）は一般的に起こりうる問題で, 特定のタスクに関するデータセットがとても少ない場合などに発生する.

Meta-Learning: Bilevel Optimization View

さて, さきのTask-Distribution Viewは, メタ学習の理論面での説明であった. つまり, 一般的なメタ学習のフローであるが, それゆえに, 実装面での説明は欠いている.

Bilevel Optimization Viewでは, Meta-training stageやMeta-testing stageの数式をどう解いていくのか？というのを説明する.

結論をのべると, Meta-training stageを, Meta-testing stageを制約として捉えた, Bi-Level最適化問題として扱うのだ.

つまり, 以下の制約付き最適化問題を解く.

\begin{align} w^{*} &= \argmin_{w} \sum^{M}_{i=1}L^{meta}(\theta^{* (i)}(w), w, D^{val(i)}_{source}) \\ \mathrm{s.t.} \theta^{*(i)} &= \argmin_{\theta} L^{task}(\theta, w, D^{train(i)}_{source}) \end{align}

実際には, 二段階構成でこの最適化問題をとく. それぞれ, inner-loopとouter-loopと呼ぶ. 具体的には, メタ知識wと, 学習モデルのパラメータ\thetaを別々に最適化していく.

Inner-Loop

Inner-loopでは, 各タスクに対するパラメータ(\theta)適応を実行する(Eq(6)).

ここでは, メタ知識wについては固定しておき, その状態で各タスクに対する最適化なパラメータ\theta^{*(i)}を学習する.

Outer-Loop

Outer-loopでは, タスク間のメタパラメータ(w)を最適化している.
今度は, Inner-loopで獲得した各タスクに対する最適化なパラメータ\theta^{*(i)}を固定しておき, 全タスクに共通するメタ知識wに関する最適化を行う.

Meta-Learning: Feed-Forward Model View

メタ学習の基本理論(Eq(2))を,二段階最適化問題(Bi-level Optimization)として解くというアプローチは代表的ではあるが, 実際には他にもさまざまなアプローチが存在する.

こうしたアプローチを抽象的に捉えようとするのが, Feed-Forward Model Viewの話である.

その特徴として,

  • Meta Learnerを単なる「関数」 としてみなす
  • メタ学習は. 入力（例えばタスク情報や少数の例）から出力（パラメータや予測）への 直接的な写像 を学習する

以下に, 学習モデルを線形回帰(linear regression)モデルに限定した場合の例を挙げている.

\begin{align} \min_{w} \mathbb{E}_{T \sim p(T), (D^{tr}, D^{val}) \in T} \sum_{(x,y)\in D^{val}} \lbrack (x^T g_w(D^{tr}) - y )^2\rbrack \end{align}

この式では, 学習データセットD^{tr}を関数g_{w}により埋め込み, 線形回帰モデルでの重みとして扱っている. (入力xから出力yを予測するときのモデルの重み）

つまりは, 入力データを関数g_{w}を通して直接的な写像を獲得し, この埋め込み表現とラベルの関係を予測するという順方向の学習方法となっている(feed-forwardのEnd-to-End学習)

ひとつの式で完結しており, 二段階最適化と異なって, Inner loopが存在しない（or きわめて浅い）ことが多く, 再帰的構造や外部メモリで汎化を実現している.

ここまでの整理

  • Task-Distribution Viewは, より理論的な枠組みや目的の定義に近い
  • Bilevel Optimization Viewは, その理論を実装に落とし込んだ形式で. 多くのメタ学習アルゴリズムがこの構造を持つ
  • Feed-Forward Viewは, Inner loopの明示的な最適化を避け, 入力→出力のマッピングでメタ知識を直接学習する実装寄りの形式です。
観点 Task-Distribution View Bilevel Optimization View Feed-Forward Model View
着目点 タスク分布上での汎化 階層的な最適化（inner/outer loop） 関数としてのメタラーナー
最適化の形式 期待損失の最小化 二段階最適化構造 通常は end-to-end 学習
Inner loop（タスク内学習） 存在（暗黙的） 明確に存在 通常は存在しない or メモリに依存
実装の例 MAML, ProtoNet MAML, Meta-SGD MANN, MetaNet, SNAIL, Reptile, etc.
応用分野 few-shot, multi-task few-shot, continual learning 強化学習、迅速予測

MAML (Model-Agnostic Meta-Learning)

論文のほうではさまざまな手法が整理されているが, すべての手法を説明するのは難しいので, 代表的な二段階最適化ベースのメタ学習：MAML (Model-Agnostic Meta-Learning)を説明する.

https://arxiv.org/abs/1703.03400

そして, その特徴としては, タスクTに含めることができるものは, 勾配計算ができるもの, つまりは微分可能な仕組みであればなんでもよい, としている点で, とても汎用性の高いメタ学習の仕組みとなっていることがわかる.
タイトルのModel-Agnostic (モデルに非依存)　というのはそういう意味である.

そのため, 各タスク(回帰,分類,強化学習など)は以下のようなTの構造で表現する.

\begin{align} T = \{L(x_1, a_1, \cdots, x_H, a_H), q(x_1), q(x_{t+1}|x_t,a_t),H\} \end{align}

それぞれのタスクは, 損失関数L, 初期分布q(x_1), 遷移確率分布q(x_{t+1}|x_t, a_t), エピソード長さHから構成されている.

ただ, 分類や回帰問題などの教師あり学習の系統では, H=1となるため, 遷移確率分布は不要となる.[1]

また, 適応したいタスクの分布を表現したタスク分布p(T)を導入する.

アルゴリズム全体としては, 二段階最適化(Bi-level Optimization) を使用したものとなっている.

  1. 収束するまで以下の処理を繰り返す
    2. バッチサイズでタスクをp(T)からサンプリング(=T_i)
    3. サンプリングされたタスクT_iすべてで以下を行う
    3-1. タスクT_iに関するK個のデータサンプルを取得し, \nabla_{\theta}L_{T_i}(f_{\theta})を計算する
    3-2. 勾配計算で, \theta^{'}_{i} = \theta - \alpha\nabla_{\theta}L_{T_i}(f_{\theta})を求める
    4. タスクT_iのそれぞれに対する勾配計算を終えたあと, メタ的に最適化を以下の式により行う. \theta \leftarrow \theta - \beta \nabla_{\theta}\sum_{T_{i} \sim p(T)}L_{T_i}(f_{\theta^{'}_{i}})

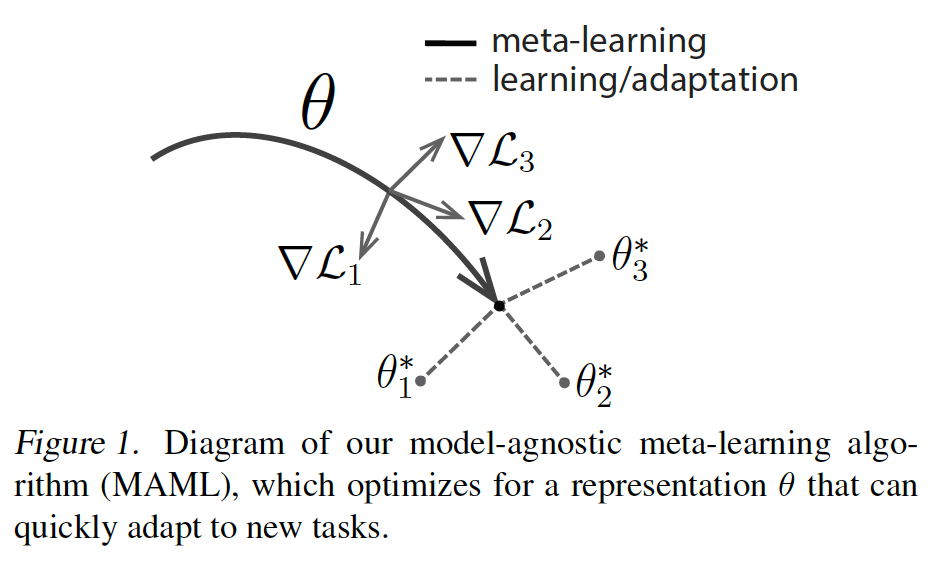
イメージとしては, 論文中のこの図を参照するとよい.
キャップションにもあるように, メタ知識\thetaは, 複数のタスクT_1,T_2,T_3に即座に適応できるような場所を探す.

そして, 新規のタスクに出会した時には, メタ知識\thetaからスタートして学習を進めると, 早く学習が収束できる...ということである.

メタ知識\thetaに求められる性能を考えれば, 複数のタスクに瞬時適応できるような（ベースとなる）値でなければいけない. そんな値を探すために, 学習時には複数のタスクに良い塩梅で適応できる\thetaを勾配から求めているのだろう.

論文単体での説明については以下が詳しいので参照してほしい.
https://qiita.com/ku2482/items/ee2fd87bbb5353664f59

https://qiita.com/skillup_ai/items/bf027df2afbb3e593196

口語的に理解しやすくした記事①

https://qiita.com/25226153/items/bf37c8ce5f128897e9e7

口語的に理解しやすくした記事②

Neural Processes

メタ学習の汎用的な手法を提案したMAMLであったが, 計算コストの高さが課題にされていた. それを克服しようと提案されたのが, Garneto et al., 2018によるNeural Processesである.

https://arxiv.org/abs/1807.01622

Neural Processesは, タスク条件付き確率過程をニューラルネットでモデル(NN)化し, 入力のコンテキストセットから全関数を推定する分布モデルを学習できる.

Gaussian Processのように不確実性を扱いつつ, それをNNで計算することで,効率よく計算できる.

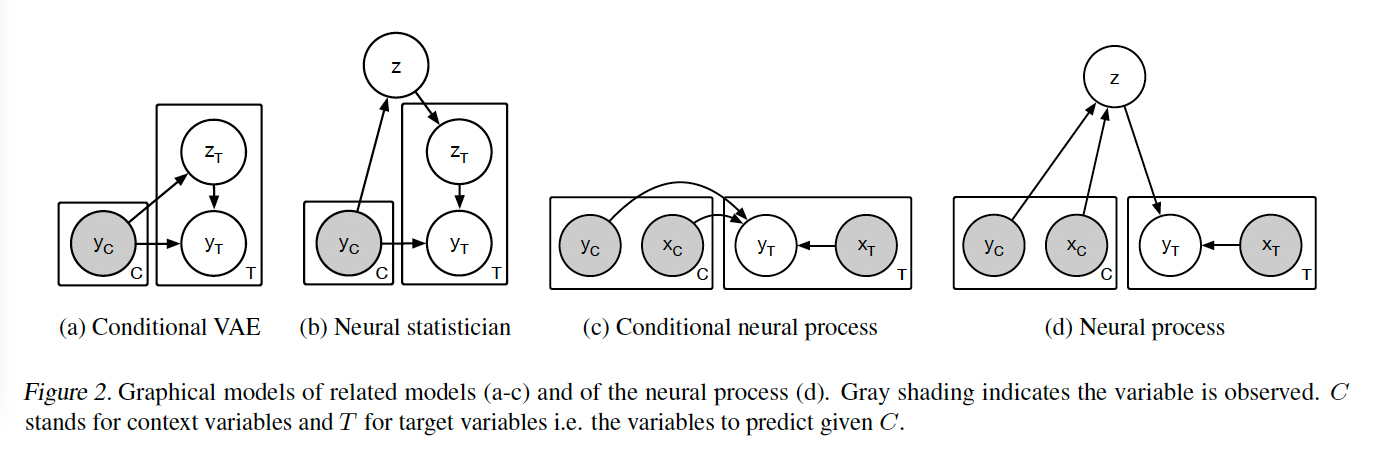
Neural Processesのやっていることの概要を説明する.
コンテキスト観測データC = (X_C, Y_C) = {(x_i, y_i)}_{i \in L(C)} をもちいて,潜在変数zの条件付き事前確率P(z|C)を求める. ここで,zはタスクのことである.
そして,予測したラベル,つまりターゲットデータD=(X,Y)={(x_i, y_i)}_{i \in L(D)}が与えられると,さきほどの潜在変数zを用いて, 予測モデルp(y_i | x_i, z)を求める.
一連の生成過程は以下の式で表される.

\begin{align} P(Y|X,C) = \int P(Y|X,z)P(z|C)dz \end{align}

Feed‑Forward Model View に分類される典型例で, MAMLのようなInner Loop を持たず, タスク（support set）をエンコーダに入力→予測が一発で完結する設計となっている.

Neural Processesをメタ学習の一種だといっている以下の論文は参考になる.
https://proceedings.neurips.cc/paper_files/paper/2019/file/110209d8fae7417509ba71ad97c17639-Paper.pdf

Neural Processes(NPs)をはじめ, Neural Process familyもボリュームが膨大なので説明はこの程度にしておく.

https://xyzml.medium.com/neural-processes-explained-2bd9b225412b

Neural Processes の海外説明記事

https://www.slideshare.net/slideshow/dlthe-neural-process-familyneural-processes/141533902

Neural Process Familyの比較やお気持ち紹介スライド

https://xtech.nikkei.com/atcl/nxt/mag/rob/18/00007/00009/

メタ学習系のお話の記事

類似領域

サーベイ論文内で紹介されていたメタ学習と類似した分野について整理しておく.

領域 目的 アプローチの焦点 メタラーニングとの違い
Meta-Learning タスク横断的に学習・適応戦略を獲得 内部学習アルゴリズムや初期化を改良／最適化 複数タスクにまたがる汎化能力とAdaptation性能
Transfer Learning 既存モデルの再利用 転移可能なモデルまたは特徴学習 タスク一般化よりはパラメータ再利用が中心
Multi-task Learning 複数タスクの同時学習 共通表現の共有 適応能力より同時学習による表現共有が主目的
Hyperparameter Optimization モデル性能のために設定を調整 単一タスクにおける最適ハイパーパラメータ探索 タスクの汎用戦略設計ではない
Domain Adaptation 分布の異なるターゲット環境への適応 微調整・再トレーニング タスク戦略の汎用化より特定ドメイン適応
AutoML モデル構造・探索自動化 タスクごとの最適モデル探索 アルゴリズムそのものの学習ではない
Curriculum Learning 難易度順管理による効率学習 訓練データの順序設定 学習過程の設計であり、metaの戦略とは異なる

Transfer Learning（転移学習; TL）

概要：事前に学習したモデルや特徴表現を別のタスクに再利用して, 初期性能を向上させる手法.
違い：メタ学習が「学習アルゴリズム自体を改良」するのに対し, 転移学習は主にモデルパラメータの再利用が中心
メタ学習ではタスクの自動適応速度や汎化力を向上させることにも着目.

Multi-task Learning（多タスク学習）

概要：複数タスクを同時に学習することで, 共有表現（共通の特徴） を獲得し, 各タスクの性能を改善する手法. 似たようなタスクであれば, パラメータのシェアができるでしょ？というもの.
違い：多タスク学習は同時に複数タスク学習する一段階の学習プロセスなので, メタ学習のようなタスク間での高速適応能力は対象外

Hyperparameter Optimization（ハイパーパラメータ最適化; HO）

概要：学習率や正則化係数などのハイパーパラメータを最適化する手法. グリッド探索やベイズ最適化などが一般的. ハイパーパラメータが,how to learnを代用するという意味では, HOもメタ学習に近い.
違い：ハイパーパラメータ最適化は, 単一タスクやモデルに対して設定を調整する手法であり, 複数タスクへの汎用性や適応力の獲得は主目的ではない.

Domain Adaptation（ドメイン適応）

概要：あるドメイン（例：画像や言語環境）で訓練されたモデルを, 異なるデータ分布に適用できるよう調整する技術。
違い：多くはモデルの改変や微調整が必要だが, メタ学習はタスクを抽象した再利用可能な学習戦略を獲得することに重点を置く. つまりは, パラメータのその根底にあるハイパーパラメータを対象とするかどうかである.

ドメイン適応も, 結局転移学習の一種であるため（場合にはよって同定義されるらしく),　TLと似た差別化要素をもつが,,, あまり区別ができなくなっている💦

https://zenn.dev/monchy1017/articles/0c725f1d981881

ドメイン適応と転移学習の違いはこちらを確認

AutoML（自動機械学習）

概要：適切なモデル構造, 特徴設計, ハイパーパラメータなどを自動探索するシステム.
違い：AutoML は特定タスクに対する自動チューニングが主目的であるのに対し, メタラーニングは複数タスクで使える学習アルゴリズムそのものの汎用化・自動化を目指す (より複数のタスクへの適用）

Curriculum / Self-Paced Learning（カリキュラム学習、自律的順序学習）

概要：学習例の難易度を段階的に上げながらモデルを訓練する手法/
違い：教材や学習順序の管理でモデルの学習効率を上げる手法であり, 学習プロセスそのものの改良（メタ学習）は対象外

メタ的に学習するLLMへと--

メタ学習に関するサーベイ論文については離れるが, ここまでメタ学習の目指すものや理論についてざっと見てきた. 何度も触れてきたが, メタ学習は「学習方法を学習する枠組み」 であり, さまざまなタスクへの適応力・速度をあげる仕組みだ.

メタ学習が世間的にトレンドになったのは,2018-2020年ぐらいな気がする.
最近だと,基盤モデル(FM)としてのLLMがトレンドであるが, メタ学習とLLMとの関連性や違いはなんだろうか？とふと疑問に思ってしまった.

MAML-en-LLM

「メタ学習とLLM」みたいなキーワードを日本語で検索してもヒットしないので英語で検索すると以下のような論文がでてきた. "MAML-en-LLM: Model Agnostic Meta-Training of LLMs for Improved In-Context Learning"とのことで, タイトル通り, 「メタ学習+LLM」の融合手法のようだ.

詳細は省くが以下のような内容.

概要

  • 目的：事前学習済みの大規模言語モデル（LLM）に 二段階最適化（MAML） を適用し、未見タスクへのインコンテキスト学習（ICL）性能を強化すること
  • 従来の MetaICL や MetaICT は、多様タスクでマルチタスク的に fine-tuning するのみで, 真の意味で汎化する初期パラメータを学習するわけではないと指摘
  • MAML‑en‑LLM は Inner Loop（タスク個別適応）＋ Outer Loop（メタ更新）という標準的な MAML フレームを LLM に適用し, 汎化可能な初期パラメータを習得する手法

🧑‍💻LLM視点でなぜメタ学習が必要なのか

  • 問題設定：LLM は in-context learning（prompt に few-shot 例を与えるだけで適応）でタスク解決することができるが, 初期パラメータのままでは適応性能が限定的
  • 提案手法：LLM に対して多タスク warm-up を施すのではなく、※ meta-learning によって adaptation を通じて良い初期点 θ を学習
  • 利点:
    • 見たことのないタスクでの汎化精度が +2% 向上
    • 適応性能（few-shot 設定）では +4% の改善を実現
    • データが少ない low-resource 環境でも効果を維持
視点 新規性・貢献点
Meta-Learning 従来LLMベース手法に MAML を適用した初の実証的/構造的アプローチ
LLM / ICL 真に汎化可能なパラメータを meta-train することで、 unseen タスク適応性を向上

LCM

明示的にメタ学習を組み込むMAML-en-LLMと異なり, LCM(Large Concept Model)というのがMetaから提案されている.

詳細は以下の記事を参照してほしいが, もっと概念ベースでの理解や生成ができるようだ. 学習理論であるメタ学習とはもしかしたら関係ないかも？（💦）

https://zenn.dev/galirage/articles/meta-large-concept-model-lcm

まとめ

今回はメタ学習について,サーベイ論文を参照しながらさっとお気持ちを説明した.
メタ学習自体, トレンドになったのは,もう昔のようだが, いまでも重要な概念なので学びを深めるよい機会になった.
機会があれば, Neural Processesあたりをまた調べていきたい.

脚注

  1. いろいろなタスクの問題設定に適用できるよう組み込んだものと考えられる. ↩︎

Discussion