📉

SVMのカーネル関数って何だ？（備忘録）

2022/07/25に公開

機械学習

R. Torres, S. Takeuchi et al., “Inquiry Classification in a Speech-Oriented Guidance System Using Discriminative Learning,” IPSJ SIG Technical Report, vol.2009-SLP-77, no.13, 2009. http://id.nii.ac.jp/1001/00062674/

の研究報告を読んでいるときに以下のカーネル関数が出てきました。

\kappa(\bm{x}_i,\bm{x}_j)=(\bm{x}_{i}^{T} \bm{x}_j + 1)^d \tag{0}

カーネル関数が内積をしていることは、式から分かったのですが、これが、Support Vector Machine (SVM) を使うときに、どのような利点があるか分からなかったので、調べて自分なりにまとめました。
数式メインで書かれている資料は、沢山インターネット上にありますので、出来るだけ図と文章を多く簡潔に書きたいと思います。
ちなみに、(0)式は多項式カーネルというそうです^[1]。

機械学習初心者なので、間違いなどがありましたらコメントにて、ご指摘いただけると幸いです。

カーネル関数

そもそも、カーネル関数とは、何なんでしょうか？
色々とインターネットで調べたのですが、バシッと「これ！」という定義が見つかりませんでした。
しかし、カーネル関数を使ったカーネル法については説明がありましたので、引用します。

同志社大学データサイエンス研究室、金明哲教授の説明^[2]によるとカーネル法とは。

カーネル (kernel) 法は、データを高次元に射影し、線形問題に置き換えると同時に計算量の問題を解決する技法である。

ということだそうです。

この説明から、カーネル関数は、解析対象のデータが存在する次元では分離（分類）が出来ないものを、分離（分類）出来るように高次元に射影する関数と言えそうです。

線形カーネル

この章では、金明哲教授の記事^[2:1]の問題を、ぷるうぬす@Prunus1350さんのスライド^[3]の説明で解いて、線形カーネルを作成していきたいと思います。

問題

今、以下のようなデータがあったとします。

カテゴリ	データ1	データ2
A	(-1,-1)	(1,1)
B	(-1,1)	(1,-1)

このデータをカテゴリAとカテゴリBに分類する平面（または直線）を求めたいと思います。

ひとまず、このデータをプロットしてみると以下の図のようになります。

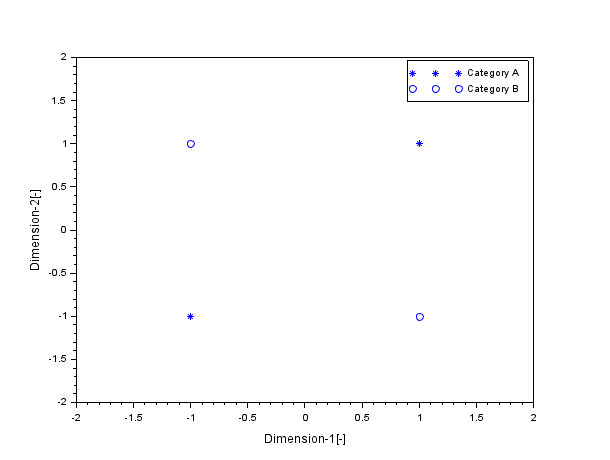
Data Plot
元データのプロット

このように。カテゴリAとカテゴリBを分離する直線を引くのは無理です。
このデータを、うまく分離できる次元に上げるカーネル関数を作っていきます。

カーネル関数の作成と解

カーネル関数には多くの種類があるのですが、一番簡単な線形カーネルを例に出します。線形カーネル関数は(1)式で表されます。

\kappa(\bm{x},\bm{z})=(\bm{x}^{T} \bm{z})^d \tag{1}

$d$ はハイパーパラメータです。
本来は、期待通りに分類できるdを探索するのですが、ここでは天下り的に $d=2$ とします。
そして、例えば $\bm{x} = (x_1, x_2)$ 、 $z=(z_1, z_2)$ とすると

\begin{aligned} \kappa(\bm{x},\bm{z}) &= (\bm{x}^{T} \bm{z})^2 \\ &= (x_{1} z_{1} + x_{2} z_{2})^2 \\ &= x_1^2 z_1^2 + 2 x_1 z_1 x_2 z_2 + x_2^2 z_2^2 \\ &= (x_1^2 , \sqrt{2} x_1 x_2 , x_2^2)(z_1^2 , \sqrt{2} z_1 z_2 , z_2^2)^T \tag{2} \end{aligned}

ここで $\phi(\bm{x})=(x_1^2 , \sqrt{2} x_1 x_2 , x_2^2)^T$ , $\phi(\bm{z})=(z_1^2 , \sqrt{2} z_1 z_2 , z_2^2)^T$ とすると(2)式は

\kappa(\bm{x},\bm{z}) = \phi(\bm{x})^T\phi(\bm{z}) \tag{3}

となります。このように、2次元のデータを3次元に上げることに成功しました。
では、 $\bm{x}$ をデータ1、 $\bm{z}$ をデータ2として、(3)式をプロットしてみましょう。

kernel plot
カーネル関数を使って3次元に射影したデータプロット

赤色のメッシュで示した平面で、カテゴリAとカテゴリBをうまく分離できそうです。

このように、入力データの次元だとうまく分離することが出来ないものを、分離できる次元へ上げる関数がカーネル関数です。

参考

以下、参考になったサイトを紹介します。

脚注

広島市立大学集中講義カーネル法と深層学習の数理 / 鈴木大慈 http://ibis.t.u-tokyo.ac.jp/suzuki/lecture/2020/intensive/%E8%AC%9B%E7%BE%A92_0.pdf （2022-07-25閲覧） ↩︎
Rとカーネル法・サポートベクターマシン / 金　明哲 (Jin Mingzhe) https://www1.doshisha.ac.jp/~mjin/R/Chap_31/31.html （2022-07-25閲覧） ↩︎ ↩︎
パターン認識と機械学習 §6.2 カーネル関数の構成 / ぷるうぬす@Prunus1350 https://www.slideshare.net/Prunus1350/prml-62 （2022-07-25閲覧） ↩︎

カーネル関数

線形カーネル

問題

カーネル関数の作成と解

参考

Discussion