単純ベイズ（ナイーブベイズ）を1から実装した【車輪の再発明】

この記事のライセンスはクリエイティブ・コモンズ・ライセンスのAttribution 4.0 International (CC BY 4.0) です。
コモンズ証（日本語）　リーガルコード（日本語）

今は便利なライブラリがあるのですが、単純ベイズ（ナイーブベイズ、Naive Bayes）を1から実装してみようと趣味で実装してみました。
昔、研究でMATLABを使って実装したことがあるのですが、だいぶ忘れてしまっていて、実装にだいぶ時間がかかってしまい…将来の自分が見返しても分かるように、数式を交えて丁寧に書きたいと思います。
記事中で注釈として示していますが、この記事を書くにあたって参考にした書籍や記事を最終章に紹介しています。

読む前に知っておいて欲しい数式と、その導出（式番号1.x）

ベイズの定理（公式）

$$p(A|B)=\frac{p(B|A)p(A)}{p(B)} \tag{1.1}$$

まず、知っておいて欲しい式は「ベイズの定理（公式）」です。
ここでは導出を書きませんが、『基礎からのベイズ統計学』^[1]に導出があり、分かりやすいです。

同時確率の分割

$A_1$と$A_2$が互いに独立の時、$A_1$と$A_2$の同時確率$p(A_1,A_2)$

$$p(A_1,A_2)=p(A_1)p(A_2) \tag{1.2}$$

で表される^[2]。

条件付き確率の分割

$A_1$と$A_2$が互いに独立の時、条件付き確率$p(A_1,A_2|B)$は以下のように分割できる^[2:1]。

$$p(A_1,A_2|B)=p(A_1|B)p(A_2|B) \tag{1.3}$$

単純ベイズの基本（数式の導出）

それでは、単純ベイズで使用する式を導出します。今回は単純ベイズを用いて入力された文章（テストデータ）を最も類似する本へ分類する、という例を用います。
ですので、「単語」と「本」というワードが出てきます。

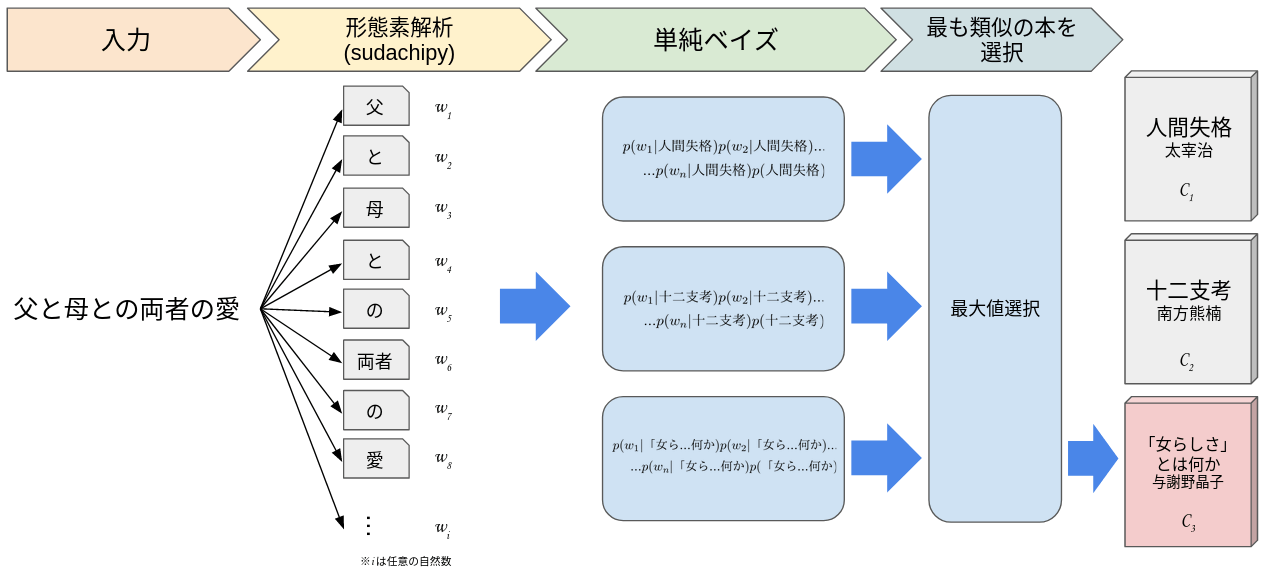
図1 単純ベイズを用いて入力文章を最も類似する本へ分類する

導出なんて要らない、結論が欲しい！という人もいらっしゃるかと思いますので、まず初めに、結論から書きます。
入力文章を形態素解析した単語を$w_i$、分類する本（カテゴリ）を$C_j$とします。ただし、$i$は文章に含まれる単語数（ここでは$n$）までの自然数、$j$は分類する本の数までの自然数とします。
以上の条件で、入力文章が$C_j$である確率を算出する単純ベイズの式は(2.1)式で表せます。
$\propto$は左辺は右辺に比例するという比例記号です。

$$p(C_j|w_1,w_2...w_n) \propto p(w_1|C_j)p(w_2|C_j)...p(w_n|C_j)p(C_j) \tag{2.1}$$

実装の章では、この(2.1)式を使って実装をしていきます。
ここから導出をしますが、導出に必要な公式は、先の章の「読む前に知っておいて欲しい数式と、その導出」に記載しています。参照する式番号(1.x)は、ここから参照しています。

まず、ベイズの公式(1.1)式を拡張して、単純ベイズの基本となる式を立てます。
入力された文章が$C_1$の本に分類される確率は、言い換えると入力された文章の条件のもと$C_1$である条件確率です。つまり$p(C_1|入力文章)$を求めます。入力文章に3つの単語$w_1,w_2,w_3$があったとき、これらの単語が$C_1$の本に含まれていそうかという$p(C_1|w_1,w_2,w_3)$を算出します。(1.1)式より

$$p(C_1|w_1,w_2,w_3)=\frac{p(w_1,w_2,w_3|C_1)p(C_1)}{p(w_1,w_2,w_3)} \tag{2.2}$$

となります。以下では$p(C_1|w_1,w_2,w_3)$を「類似度」と呼びます。
ここで、$w_1, w_2, w_3$が独立であると仮定すると、(2.2)式は以下のように書き換えることが出来ます（(1.2)式と(1.3)式を用いて）。

$$p(C_1|w_1,w_2,w_3)=\frac{p(w_1|C_1)p(w_2|C_1)p(w_3|C_1)p(C_1)}{p(w_1)p(w_2)p(w_3)} \tag{2.3}$$

分母は、本の中の文章、つまり学習データから算出される定数値で一定であるので、1としても良いです。ただし、右辺と左辺は$=$で結ぶのではなく$\propto$で結ぶようになります。
よって、(2.3)式は(2.4)式のように表せます。

$$p(C_1|w_1,w_2,w_3) \propto p(w_1|C_1)p(w_2|C_1)p(w_3|C_1)p(C_1) \tag{2.4}$$

それでは、この式を一般化します。分類するカテゴリ（ここでは本）は$m$個あり、入力された文章には単語が$n$個含まれているとすると、一番始めに示した(2.1)式のように表せます。

$$p(C_j|w_1,w_2...w_n) \propto p(w_1|C_j)p(w_2|C_j)...p(w_n|C_j)p(C_j) \tag{2.1}$$

この式の右辺にある確率は、いずれも学習データ（ここでは、本の文章）を基に算出されます。$p(w_i|C_j)$は入力文章から得られた単語$w_i$が$C_j$に出現する条件確率です。同様に、$p(C_j)$は$C_j$カテゴリ（ここでは、本の題名）が選択される確率です。

つまり、(2.1)式を解釈すると、テストデータ（入力された文章）の単語$w_1,w_2,...,w_n$の下で$C_j$が出現する条件付き確率（左辺）は、学習データを基に算出された$p(w_i|C_j)$と$p(C_j)$の積で表されます。

この計算結果を、全ての$j$で行い、一番大きい要素が分類結果となります。つまり、(2.6)式の式で分類結果を表せることになります。

$$j = \argmax{p(C_j|w_1,w_2...w_n)} \tag{2.6}$$

続いて、この式を基に実装していきます。

実装のためのテクニック

さて、それでは(2.1)式と(2.6)式を用いて実装していきます。
しかし、実装においては、いくつかテクニックが必要となります。今回、気をつけないといけないのは「ゼロ頻度問題」と「アンダーフロー対策」です。
まずは、これについて説明したいと思います。
これらの、解説はデータサイエンス情報局の記事^[3]を参考にしましたが、コードの実装を見越して、いくつかの式を書き換えています。
この章では、テストデータが学習データの学校カテゴリに分類される可能性（類似度）を算出します。

学習データとテストデータ

本章で用いる学習データとテストデータを示します。

学習データ

• 学校カテゴリ
  • 私は試験のために勉強します。
  • 来週、歴史の試験がある。
  • 私は理科の成績が良いです。
• 病院カテゴリ
  • 頭痛がひどいので痛み止めが欲しい。
  • 熱と咳がひどいです。

学校カテゴリを構成する単語は「私」「試験」「勉強」「来週」「歴史」「試験」「私」「理科」「成績」「良い」の10個とします。つまり、各単語の出現確率は

$$[私,試験,勉強,来週,歴史,理科,成績,良い] = [\frac{2}{10},\frac{2}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10}] \tag{3.1}$$

となります。

テストデータ

• 私は来月の試験のために勉強します。

テストデータに含まれる単語は「私」「来月」「試験」「勉強」です。

ゼロ頻度問題

では早速、テストデータが学習データの学校カテゴリに分類される可能性（類似度）を算出します。
テストデータの単語が学校カテゴリ（学習データ）に出現する確率は、(3.1)式から

$$[私,来月,試験,勉強] = [\frac{2}{10},0,\frac{2}{10},\frac{1}{10}] \tag{3.2}$$

そして、学校カテゴリが学習データに出現する確率は、$\frac{3}{5}$であるので

$$p(C_{学校}) = \frac{3}{5} \tag{3.3}$$

となります。
したがって、(3.2)式、(3.3)式、(2.1)式からテストデータが学校カテゴリに分類される可能性は

$$\begin{aligned} p(C_{学校}|私,来月,試験,勉強) &= \frac{2}{10} \times 0 \times \frac{2}{10} \times \frac{1}{10} \times \frac{3}{5} \\ &= 0 \tag{3.4} \end{aligned}$$

と算出されます。
(3.4)式を見て分かるように、0頻度が項として現れると、求めたい確率も0になってしまう問題を「ゼロ頻度問題」といいます。

荷重スムージング

ゼロ頻度問題の対策として、荷重スムージングという方法が用いられます。
具体的には、(3.2)式に示す全ての分子に1を加算し、分母に学習データ全体に出現する重複を除いた全単語数を加算します。
今回は学習データに
「私」「試験」「勉強」「来週」「歴史」「理科」「成績」「良い」「頭痛」「ひどい」「痛み止め」「欲しい」「熱」「咳」「ひどい」
の15単語含まれているので、分母に15単語を足した25が入ります。

実装を見通して、(3.1)式を(3.1')式のように行列の形に書き換えておきます。
式中に出てくる$\oslash$はアダマール除算といい、行列の対応する各要素同士で除算をする記号です^[4]。

$$[私,試験,勉強,来週,歴史,理科,成績,良い] \\ = [\frac{2}{10},\frac{2}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10}] \\ = [2,2,1,1,1,1,1,1] \oslash [10,10,10,10,10,10,10,10] \tag{3.1'}$$

そして、(3.1')式を踏まえて、(3.2)式も同様に(3.2')式のように行列の形に書き換えます。

$$[私,来月,試験,勉強] \\ = [\frac{2}{10},0,\frac{2}{10},\frac{1}{10}] \\ = [2,0,2,1] \oslash [10,10,10,10] \tag{3.2'}$$

ここで、(3.2')式に荷重スムージングを適用すると

$$[私,来月,試験,勉強] \\ = ([2,0,2,1]+[1,1,1,1]) \oslash ([10,10,10,10] + [15,15,15,15]) \\ = [\frac{3}{25},\frac{1}{25}, \frac{3}{25}, \frac{2}{25}]\tag{3.5}$$

となります。(3.5)式を(3.4)式に適用すると

$$\begin{aligned} p"(C_{学校}|私,来月,試験,勉強) &= \frac{3}{25} \times \frac{1}{25} \times \frac{3}{25} \times \frac{2}{25} \times \frac{3}{5} \\ &= 2.7648e-05 \tag{3.6} \end{aligned}$$

と類似度が算出できます。
ここで注意したいのは、(3.6)式の解は確率ではありません。そのため、これまでも「類似度（可能性）」と読んでいました。ここからは、確率ではないので$p"(C_{学校}|私,来月,試験,勉強)$と表記します。

アンダーフロー対策

たったこれだけの単語数で、(3.6)式のような小さな値になってしまいます。
そのため、これ以上単語数が増えると、コンピューターでは扱えないほど桁数が増え、アンダーフロー^[5]を起こします。
その対策として、(3.6)式を対数で取ります。

$$p"(C_{学校}|私,来月,試験,勉強) = \log{(\frac{3}{25} \times \frac{1}{25} \times \frac{3}{25} \times \frac{2}{25} \times \frac{3}{5})} \\ = \log{(\frac{3}{25})} + \log{(\frac{1}{25})} + \log{(\frac{3}{25})} + \log{(\frac{2}{25})} + \log{(\frac{3}{5})} \\ = -10.49595716534263 \tag{3.7}$$

こうすれば、アンダーフローが起こる心配は無いです。ここで(3.6)式と(3.7)式の$p"(C_{学校}|私,来月,試験,勉強)$の意味は対数を取っているため、違うのですが記号が多くなるので同一表記しています。
試しに、病院カテゴリの類似度も算出してみましょう（過程は端折ります）。

$$p"(C_{病院}|私,来月,試験,勉強) = \log{(\frac{1}{22} \times \frac{1}{22} \times \frac{1}{22} \times \frac{1}{22} \times \frac{2}{5})} \\ = \log{(\frac{1}{22})} + \log{(\frac{1}{22})} + \log{(\frac{1}{22})} + \log{(\frac{1}{22})} + \log{(\frac{2}{5})} \\ = -13.280460545307417 \tag{3.8}$$

最後に、(3.7)式と(3.8)式の結果を比較すると、(3.7)式の$p"(C_{学校}|私,来月,試験,勉強)$のほうが大きいため、テストデータは学校カテゴリに分類されることが分かります。

実装（Python）

ここから、今までの式を実際にコードへ移していきます。
今回は簡単のため、学習データのカテゴリ数は3つで、それぞれのカテゴリには1文しかありません。つまり$p(C_j)$（事前確率といいます）は等しく$\frac{1}{3}$です。これを、図1の流れに従って、コードに書きます。

学習データとテストデータ

利用するデータは、青空文庫^[6]から著作権が切れた3つの本から文章を引用してきました。

学習データ

1. 『人間失格』 / 太宰治^[7]
   • 自分には、人間の生活というものが、見当つかないのです。自分は東北の田舎に生れましたので、汽車をはじめて見たのは、よほど大きくなってからでした。
2. 『十二支考』 / 南方熊楠^[8]
   • ドイツのマンハールト夥しく材料を集めて研究した所に拠れば、穀物の命は穀物と別に存し、時として或る動物、時として男、もしくは女、また小児の形を現わすというのが穀精の信念だ。
3. 『「女らしさ」とは何か』 / 与謝野晶子^[9]
   • 私は女子が「妊娠する」という一事を除けば、男女の性別に由って宿命的に課せられている分業というものを見出すことが出来ません。

テストデータ

• 自分の父は、東京に用事の多いひとでしたので、上野の桜木町に別荘を持っていて、月の大半は東京のその別荘で暮していました。
• しかるところ、黄色の衣を着、黄牛に車を牽かせて乗り、従者ことごとく黄色な人が通り掛かり、小児を見るとすなわち穀賊何故ここに坐し居るかと問うた。
• 「女らしさ」というものは、要するに私のいわゆる「人間性」に吸収し還元されてしまうものです。

実装コード

実装コードはColabとGitHubで公開しています。
Colabでは、ブラウザで実行できるので、こちらを利用することをオススメします。
共有しているコードでは、上記の数式を基に作成した自作プログラムself-made.pyと、比較用にscikit-learn^[10]の単純ベイズライブラリを用いたsklearn-sample.pyを作成しています。
これらの、コードを実行すると、図2のような出力が得られます。

図2 実行結果

図2を見て分かるように、scikitlearnの結果と自作プログラムの結果が同じで、テストデータと学習データの最も高い類似度のカテゴリが一致しているので、今回のコードは正しく動作してそうです。
では、以下で簡単に解説していきたいと思います。

Colabでの実行

Colabでコードを共有しており、ブラウザで実行して確認できます。
https://colab.research.google.com/drive/1f0MKPdC9NUNiZ44Ws1dlvb3IMPBHY8zO?usp=sharing

GitHub

GitHubでコードを共有しています。
https://github.com/KASHIHARAAkira/naive-bayes-python

全体のコードは、この節の最後で貼り付けます。その前に、コードの主要部分を解説をしていこうと思います。

解説

line95-100

ここの部分は(3.2')式の部分を実装しています。１点違うのは、コード上では0とならない項のみのベクトルと0となる項のみのベクトルを分けています。

    freq_learning_matched = freq_learning[i][num_arr_matched]  # テストデータで一致した学習データの出現頻度
    num_matched = matched_words[j][num_arr_matched]  # 学習データと一致したテストデータでの単語出現頻度

    len_non_zero_matched_words = np.sum(num_matched)  # テストデータで学習データと一致した単語の出現数（分子が0ではない要素の数）
    num_testing_words = total_each_class_testing[j] # テストデータの全体の単語数, 行列の長さになる
    len_zero_arr = num_testing_words - len_non_zero_matched_words # 要素がゼロの配列の長さ

line102-121

ここで、荷重スムージングを行った分子と分母を分けて作り、それを合わせてベクトルを作っています。(3.5)式に対応します。
ここで注意したいのは、式では各単語の出現確率$p(w_i|C_j)$を一つずつ掛けていますが、scikit-learnから学習データで出現した単語が、テストデータでいくつ出現したかをベクトルで得るので、この数だけの乗数で乗算します。

    # 荷重スムージング
    # 非ゼロ要素の分子処理
    non_zero_smooth = freq_learning_matched + 1

    num = 0
    for item in num_matched:
      non_zero_smooth[num] = non_zero_smooth[num] ** item
      num = num + 1
    # ゼロの要素を足す
    pwc = np.append(non_zero_smooth, np.ones(len_zero_arr)) #分子が出来た

    # 分母を作る
    val_deno = np.sum(freq_learning[i]) # 分母となる基本の数（荷重スムージング前）
    len_learning = len(freq_learning[i]) # 学習データ全体に出現する単語から重複を抜いた数

    deno = np.array([])
    for item in num_matched:
      deno = np.append(deno, (val_deno + len_learning) ** item)
    deno = np.append(deno, np.full(len_zero_arr, (val_deno + len_learning)))
    members = pwc / deno

line1022

最後に対数を取って、結果を得ます。(3.7)式に対応します。

    result_arr = np.append(result_arr, np.sum(np.log(members)) + np.log(pC[i]))

全体のコード

self-made.py

import time
from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import CountVectorizer
from sudachipy import dictionary
from sudachipy import tokenizer
import numpy as np

##### _φ(･_･ 自作箇所 #####

start_time = time.time()

# 学習データ（上から、人間失格、十二支考、「女らしさ」とは何か）
learning = [
    "自分には、人間の生活というものが、見当つかないのです。自分は東北の田舎に生れましたので、汽車をはじめて見たのは、よほど大きくなってからでした。",
    "ドイツのマンハールト夥しく材料を集めて研究した所に拠れば、穀物の命は穀物と別に存し、時として或る動物、時として男、もしくは女、また小児の形を現わすというのが穀精の信念だ。",
    "私は女子が「妊娠する」という一事を除けば、男女の性別に由って宿命的に課せられている分業というものを見出すことが出来ません。",
]

# テストデータ（上から、人間失格、十二支考、「女らしさ」とは何か）
testing = [
    "自分の父は、東京に用事の多いひとでしたので、上野の桜木町に別荘を持っていて、月の大半は東京のその別荘で暮していました。",
    "しかるところ、黄色の衣を着、黄牛に車を牽かせて乗り、従者ことごとく黄色な人が通り掛かり、小児を見るとすなわち穀賊何故ここに坐し居るかと問うた。",
    "「女らしさ」というものは、要するに私のいわゆる「人間性」に吸収し還元されてしまうものです。",
]

# カテゴリ（クラス）名
class_name = [
    "A 『人間失格』",
    "B 『十二支考』",
    "C 『「女らしさ」とは何か』",
]

# 事前確率（今回は全て1/3）
pC = [1/3, 1/3, 1/3]

# 形態素解析をするclass
class Morphology:
  def __init__(self, arr_title):
    self.data = arr_title
    self.cv = CountVectorizer(analyzer=self.split_words)
    self.cv.fit(arr_title)

    self.clf = MultinomialNB()
    self.xs = []

    for item in arr_title:
        self.xs.append(self.cv.transform([item]).toarray())
    X = np.concatenate(self.xs)
    self.clf.fit(X, [i for i in range(1, len(arr_title)+1)])

  def split_words(self, text):
    tokenizer_obj = dictionary.Dictionary().create()
    mode = tokenizer.Tokenizer.SplitMode.C
    return [m.surface() for m in tokenizer_obj.tokenize(text, mode)]

  def get_vocabulary(self):
    return self.cv.vocabulary_

  def get_words_frequency(self):
    return self.cv.transform(self.data).toarray()

  def get_matched_words(self, text):
    return self.cv.transform(text).toarray()

# 学習データを形態素解析するために初期化
morphology_learning = Morphology(learning)

# 学習データの単語一覧
words_list_learning = morphology_learning.get_vocabulary()

# 事前確率（単語の出現頻度）の定義
freq_learning = morphology_learning.get_words_frequency() # 各単語の出現頻度
total_each_class_learning = np.sum(freq_learning, axis=1) # 各クラスの単語数

# テストデータの情報を取得
morphology_testing = Morphology(testing)

# テストデータの単語一覧
words_list_testing = morphology_testing.get_vocabulary()

# テストデータの各単語出現頻度
freq_testing = morphology_testing.get_words_frequency() # 各単語の出現頻度
total_each_class_testing = np.sum(freq_testing, axis=1)  # 各クラスの単語数

# テストデータに出現する単語で学習データに含まれる単語を抽出
matched_words = morphology_learning.get_matched_words(testing)

print("📝自作単純ベイズの結果、()は類似度が高い順番。アルファベットはカテゴリ記号、『』は書名。")
for j in range(0,len(class_name)):
  result_arr = np.array([])
  for i in range(0,len(class_name)):

    num_arr_matched = np.intersect1d(np.nonzero(freq_learning[i]), np.nonzero(matched_words[j]))

    freq_learning_matched = freq_learning[i][num_arr_matched]  # テストデータで一致した学習データの出現頻度
    num_matched = matched_words[j][num_arr_matched]  # 学習データと一致したテストデータでの単語出現頻度

    len_non_zero_matched_words = np.sum(num_matched)  # テストデータで学習データと一致した単語の出現数（分子が0ではない要素の数）
    num_testing_words = total_each_class_testing[j] # テストデータの全体の単語数, 行列の長さになる
    len_zero_arr = num_testing_words - len_non_zero_matched_words # 要素がゼロの配列の長さ

    # 荷重スムージング
    # 非ゼロ要素の分子処理
    non_zero_smooth = freq_learning_matched + 1

    num = 0
    for item in num_matched:
      non_zero_smooth[num] = non_zero_smooth[num] ** item
      num = num + 1
    # ゼロの要素を足す
    pwc = np.append(non_zero_smooth, np.ones(len_zero_arr)) #分子が出来た

    # 分母を作る
    val_deno = np.sum(freq_learning[i]) # 分母となる基本の数（荷重スムージング前）
    len_learning = len(freq_learning[i]) # 学習データ全体に出現する単語から重複を抜いた数

    deno = np.array([])
    for item in num_matched:
      deno = np.append(deno, (val_deno + len_learning) ** item)
    deno = np.append(deno, np.full(len_zero_arr, (val_deno + len_learning)))
    members = pwc / deno
    result_arr = np.append(result_arr, np.sum(np.log(members)) + np.log(pC[i]))
  print("🌟【" + class_name[j] + "】「" + testing[j] + "」の類似度が高い順番")
  num = 1
  for item in np.argsort(result_arr)[::-1]:
    print("(" + str(num) + ") " + class_name[item])
    num = num + 1
  # print(result_arr) # 類似度（対数）
print("⌛実行時間⌛ " + str(time.time() - start_time) + "秒\n")

参考文献（書籍、記事）

主要な参考文献を紹介します。

『基礎からのベイズ統計学』豊田秀樹（編著）,朝倉書店,2020

ISBN：978-4-254-12212-1
https://www.asakura.co.jp/detail.php?book_code=12212

『パターン認識と機械学習 上』C.M.ビショップ（著）,丸善出版,2015

ISBN：978-4-621-06122-0
https://www.maruzen-publishing.co.jp/item/b294524.html

『ナイーブベイズ分類器の仕組み』, データサイエンス情報局

2022-07-07閲覧　
https://analysis-navi.com/?p=3108

脚注

1. pp.3~8,豊田秀樹（編著）,基礎からのベイズ統計学,朝倉書店,2020,978-4-254-12212-1

2. pp.11,豊田秀樹（編著）,基礎からのベイズ統計学,朝倉書店,2020,978-4-254-12212-1

3. データサイエンス情報局, データ分析の手法-ナイーブベイズ分類器の仕組み- https://analysis-navi.com/?p=3108 （2022-07-07閲覧）

4. 山たー, アダマール演算子 (Hadamard operation), 知識のサラダボウル https://omedstu.jimdofree.com/2018/04/23/%E3%82%A2%E3%83%80%E3%83%9E%E3%83%BC%E3%83%AB%E6%BC%94%E7%AE%97%E5%AD%90-hadamard-operation/ （2022-07-07閲覧）

5. オーバーフローとアンダーフロー, 数値計算の基礎, 東京電機大学　工学部　情報通信工学科　ネットワークロボティクス研究室（教員：鈴木　剛 教授） http://www.nrl.c.dendai.ac.jp/edu/2019/ep2019/ep_chap02/index.html#02-02-01 （2022-07-07閲覧）

6. 青空文庫 https://www.aozora.gr.jp/

7. 太宰治, 人間失格, 青空文庫 https://www.aozora.gr.jp/cards/000035/files/301_14912.html （2022-07-07閲覧）

8. 南方熊楠, 十二支考-羊に関する民俗と伝説-, 青空文庫 https://www.aozora.gr.jp/cards/000093/files/2538_34822.html （2022-07-07閲覧）

9. 与謝野晶子,「女らしさ」とは何か, 青空文庫 https://www.aozora.gr.jp/cards/000885/files/3325_6558.html　（2022-07-07閲覧）

10. scikit-learn / Naive Bayes https://scikit-learn.org/stable/modules/naive_bayes.html （2022-07-06閲覧）