Julia言語の自動微分パッケージの比較と高階のテンソルまで計算する方法
1. はじめに
本記事では、異なる2つの自動微分パッケージの比較と、自動微分パッケージだけでは計算できない高階のテンソルまで計算する方法を紹介する。
Julia言語ではさまざまな自動微分のパッケージが開発されており、JuliaDiffというHPでまとめられている。いろいろあって迷ったが、よく使われているらしいZygote.jlかForwardDiff.jlで比較を行ってみることにする。比較においては、それぞれのパッケージによる自動微分の計算速度や計算精度について、数値微分や数式微分と合わせて比較することにする。
なお、本記事では、数式微分、数値微分、自動微分の定義や計算手法の詳細は割愛するため、興味があれば各自で調べてみるとよいだろう。もしそれぞれがよくわからないという場合は、まずは以下のイメージを持っておけば問題ないだろう。
- 数式微分:高校で学んだ微分そのもの。式が複雑だと大変。
- 数値微分:数値的に微分係数の近似値を計算する手法。微分係数を求めたい点から少し離れた2点での値を求め、2点間の傾きを計算することで微分係数とする。丸め誤差や打切り誤差から精度低下が起きたりする。
- 自動微分:上2つの手法とは異なるまったく手法。連鎖律を駆使して、真の微分係数を計算することができる手法。
2. Julia言語で自動微分をする方法
Julia言語で自動微分をする方法について以下にまとめる。
using Zygote # 自動微分パッケージ1
using ForwardDiff # 自動微分パッケージ2
using BenchmarkTools # 時間計測用
using Plots # プロット用
でまずは自動微分パッケージ(+α)を読み込んでおく。BenchmarkToolsは、実行する関数のパフォーマンスを本格的に評価できるようにするパッケージであり、実行する関数の前に@benchmarkをつけるだけで実行時間の統計値やメモリアロケーションを見ることができる非常に便利なものである。
2.1. 一変数スカラー関数の場合
さて、ある適当な一変数スカラー関数
# Zygoteの場合
df_zy(x) = f'(x)
df_zy2(x) = f''(x)
df_zy3(x) = f'''(x)
# ForwardDiffの場合
df_fd(x) = ForwardDiff.derivative(f,x)
df_fd2(x) = ForwardDiff.derivative(x -> ForwardDiff.derivative(f, x), x)
df_fd3(x) = ForwardDiff.derivative(x -> ForwardDiff.derivative(x -> ForwardDiff.derivative(f, x), x), x)
これから見てわかるように、一変数スカラー関数の一次導関数を求めようとする場合、Zygoteは'をつけるだけで自動微分ができる。高次導関数も'''のように'を追加していくだけでよいので非常に楽である。一方で、ForwardDiffのほうは、計算コードが複雑になっていくように見える(もしかしたらもっときれいに書けるのかもしれない)。ただし、計算速度はForwardDiffのほうが早く、しかも高次になるにつれてZygoteは急激に遅くなるようである。以下のコードで確認してみよう。ここでは、例として
# 関数
f(x)=x*exp(x)
# Zygoteの場合
df_zy(x) = f'(x)
df_zy2(x) = f''(x)
df_zy3(x) = f'''(x)
# ForwardDiffの場合
df_fd(x) = ForwardDiff.derivative(f,x)
df_fd2(x) = ForwardDiff.derivative(x -> ForwardDiff.derivative(f, x), x)
df_fd3(x) = ForwardDiff.derivative(x -> ForwardDiff.derivative(x -> ForwardDiff.derivative(f, x), x), x)
# 適当な数値で計算させてみる
x = 1.0
display(@benchmark df_zy1(x))
display(@benchmark df_zy2(x))
display(@benchmark df_zy3(x))
display(@benchmark df_fd1(x))
display(@benchmark df_fd2(x))
display(@benchmark df_fd3(x))

Zygoteでの実行結果
Zygoteの場合、導関数の次数の増加に対して計算時間とメモリアロケーションがともに指数的に増大しているようである。

ForwardDiffでの実行結果
ForwardDiffの場合、計算時間は導関数の次数の増加に対して線形増加のようであり、メモリアロケーションは変化していないことがわかる。また、1次導関数の場合の結果を見ても、ForwardDiffのほうが高速である。
2.2. 多変数スカラー関数の場合
多変数スカラー関数
# 関数
f(x,y) = x^5+y^5
f(xy) = f(xy[1],xy[2]) # ベクトルで入力できるようにする
xy = [1.0,2.0] # この点で評価する
# Zygoteの場合
# ヤコビ行列
j_zy(xy) = Zygote.jacobian(f,xy)
display(j_zy(xy)) # Tuple{Matrix{Float64}}
# 勾配ベクトル
g_zy(xy) = Zygote.gradient(f,xy)
display(g_zy(xy)) # Tuple{Vector{Float64}}
# ヘッセ行列
h_zy(xy) = Zygote.hessian(f,xy)
display(h_zy(xy)) # 2×2 Matrix{Float64}
# ForwardDiffの場合
# ヤコビ行列
# j_fd(xy) = ForwardDiff.jacobian(f,xy) #fが配列ではないとダメなので数値を代入したときにとエラーになる
j_fd(xy) = ForwardDiff.jacobian(xy->[f(xy)],xy) # fは配列である必要があるので無名関数で配列化
display(j_fd(xy)) # 1×2 Matrix{Float64}
# 勾配ベクトル
g_fd(xy) = ForwardDiff.gradient(f,xy)
display(g_fd(xy)) # 2-element Vector{Float64}
# ヘッセ行列
h_fd(xy) = ForwardDiff.hessian(f,xy)
display(h_fd(xy)) # 2×2 Matrix{Float64}
出力結果の型がパッケージによって微妙に異なっていることに注意が必要である。
計算速度についても比較しておこう。以下を実行する。
display(@benchmark j_zy(xy)) # Tuple{Matrix{Float64}}
display(@benchmark g_zy(xy)) # Tuple{Vector{Float64}}
display(@benchmark h_zy(xy)) # 2×2 Matrix{Float64}
display(@benchmark j_fd(xy)) # 1×2 Matrix{Float64}
display(@benchmark g_fd(xy)) # 2-element Vector{Float64}
display(@benchmark h_fd(xy)) # 2×2 Matrix{Float64}
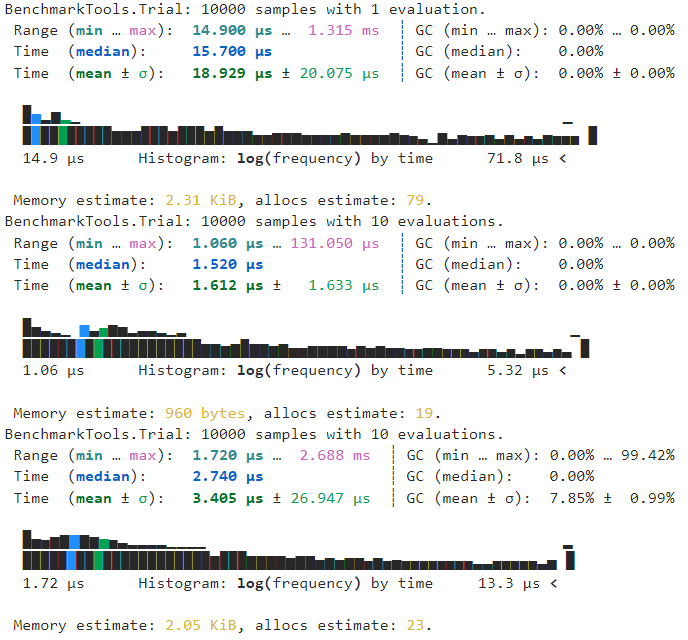
Zygoteでの実行結果

ForwardDiffでの実行結果
ZygoteとForwardDiffを比べると、ForwardDiffのほうが2倍ほど速い。そのため、計算速度を重視する場合はForwardDiffを使うのが良いだろう。
3. 数値微分・数式微分との比較
これまではパッケージごとの自動微分の実行方法や計算速度について見てきたが、ここでは自動微分vs数値微分vs数式微分での精度や計算速度について見ていこう。
3.1. 精度での比較
はじめに、自動微分と数式微分の差を確認してみよう。以下のコードを実行する。ここでは例として
# 関数と導関数の定義
f(x) = exp(x) # 微分する関数の定義
df_zy(x) = f'(x) # Zygoteの場合
df_fd(x) = ForwardDiff.derivative(f,x) # ForwardDiffの場合
x = range(0,10,101) # 適当な範囲のxで誤差を比較してみる
# 描画
plot(x,@.(df_zy(x)-f(x)),label="Zygote")
plot!(x,@.(df_fd(x)-f(x)),label="ForwardDiff")
savefig("plt1.png")# 図の保存

ZygoteとForwardDiffによる自動微分と数式微分の差
この図から、自動微分パッケージで算出されるものと数式微分で算出されるものは完全に一致していることがわかる。
一方、数値微分はどうだろうか?中心差分近似による数値微分を試してみる。
# 数値微分(中心差分近似)との比較をしてみる
# 数値微分を行う関数の定義
function nd(f)
h = eps(Float16)
return x->(f(x+h)-f(x-h))/2h
end
df_nd(x) = nd(f)(x)# 数値微分による導関数の定義
plot!(x,@.(df_nd(x)-f(x)),label="Numerical")# 描画
savefig("plt2.png")# 図の保存

数値微分と数式微分の差
この図から、数値微分ではとくに
3.2. 計算速度での比較
計算速度の比較のため、以下を実行してみよう。
y = 1.0
display(@benchmark f(y)) # 数式微分での計算速度(f'=exp(x)なのでfを使っている)
display(@benchmark df_nd(y)) # 数値微分での計算速度
display(@benchmark df_zy(y)) # 自動微分(Zygote)での計算速度
display(@benchmark df_fd(y)) # 自動微分(ForwardDiff)での計算速度
筆者の環境では以下のような計算結果になった。

平均的な計算時間(mean)で比較すると、数式微分<自動微分(ForwardDiff)<自動微分(Zygote)<数値微分という結果であった。この例では、自動微分は数式微分の約1.5倍程度、数値微分よりやや高速といった計算速度であった。
3.3. 比較のまとめ
比較結果は以下である。
- 計算精度
- 自動微分は厳密に数式微分と一致する
- 数値微分は誤差が生じる(当たり前)
- 計算速度
- 数式微分<自動微分(ForwardDiff)<自動微分(Zygote)<数値微分
このことから、もはや数値微分を使う意味はあまりなさそうであり自動微分を使うのが良いと思われる。また、自動微分を使う場合は、ZygoteよりもForwardDiffを使うほうがよさそうである。そのため、筆者としては基本的にはForwardDiffを使っていこうと考えている。
4. 高階のテンソルを計算する方法
自動微分パッケージを使って高階のテンソルを計算する方法を紹介する。自動微分パッケージのAPIにはヘッセ行列(もとのスカラー関数からすると2階のテンソル)までしか計算できない。もともとForwardDiffの古いバージョンではテンソルを計算する機能が実装されていたようだが、最新バージョンでは削除されているようである。
さて、以下のようにすればN階までのテンソルを計算することができる。なお、より洗練されたコーディングがあるかもしれないが、ひとまずはこれで動くのでよしとしておく。
function fd_tensorTillN(f, x, N)
n = length(x)
fhj_fd_list = []
fd = []
if N>=1
push!(fd,ForwardDiff.gradient(f, x)) # 1階テンソル
end
if N>=2
push!(fd,ForwardDiff.hessian(f, x)) #2階テンソル(行列)(具体的な値)
end
if N>=3
push!(fhj_fd_list,y->ForwardDiff.hessian(f, y)) #2階テンソル(行列)(関数)
for i=3:N
push!(fhj_fd_list,y->ForwardDiff.jacobian(fhj_fd_list[i-2], y)) #3階以上のテンソル(関数)を追加
temp = fhj_fd_list[end](x) # n^(i-1) × nの行列で出力されるため、これをテンソルに成形する
s1,s2=size(temp)
N = Int(log(s2,s1)) + 1
push!(fd,reshape(temp,Tuple(Int(x) for x in ones(N)*s2)))
end
end
return fd
end
# 例
f(x,y) = x^5+y^5
f(xy) = f(xy[1],xy[2])
xy = [1.0,2.0]
fd_tensorTillN(f, xy,5)
4. まとめ
本記事では、異なる2つの自動微分パッケージの比較と、自動微分パッケージだけでは計算できない高階のテンソルまで計算する方法を紹介した。これから自動微分を使って、軌道計算でいろいろ遊んでいきたいと思う。
Discussion