🐶

ABC236解説：本番でACできた問題＋1問（Python）

2022/02/05に公開

Python

A - chukodai

Pythonでは要素の交換を簡単に行なえます。

a, b = b, a

文字列を一文字ずつのリストにして、2つの文字を交換すると良いでしょう。
なお、文字の位置を指定する際には0-indexなのに注意しましょう。

実装

a.py

S = list(input())
a, b = list(map(int, input().split()))

a, b = a - 1, b - 1

S[a], S[b] = S[b], S[a]

print("".join(S))

B - Who is missing?

手持ちの枚数が3枚のカードを探します。
Counterを用いると簡単にカードの種類と要素数をまとめることができます。

制約が $1 \leq N \leq 10^{5}$ のため、for文1回で全探索ができます。

実装

b.py

from collections import Counter

N = int(input())
A = list(map(int, input().split()))

C = Counter(A)

for key, value in C.items():
    if value == 3:
        print(key)
        exit()

C - Route Map

普通列車の停車駅の中で、急行列車も止まる駅をYes、そうでない駅をNoと出力する問題です。
リストの中に特定の要素があるか探す処理は、set型を使うと高速に求まります。

実装

c.py

N, M = list(map(int, input().split()))
S = list(input().rstrip().split())
T = list(input().rstrip().split())

T = set(T)
for s in S:
    if s in T:
        print("Yes")
    else:
        print("No")

D - Dance

まず入力形式がそのままだとわかりにくいので、A[x][y]が(x,y)の相性を指すように整形します。
空白部分は $-1$ など邪魔にならない値で埋めます。

入力整形

入力整形.py

N = int(input())
A = [list(map(int, input().split())) for _ in range(2*N-1)]

for i in range(2*N-1):
    A[i] = [-1]*(i+1) + A[i]

さて、最大でも16人からなる組み合わせであることから、全探索の可能性を考えます。
実際にN=3(6人)の場合を書き出してみると、 $5\times3\times1=15$ と少なめです。

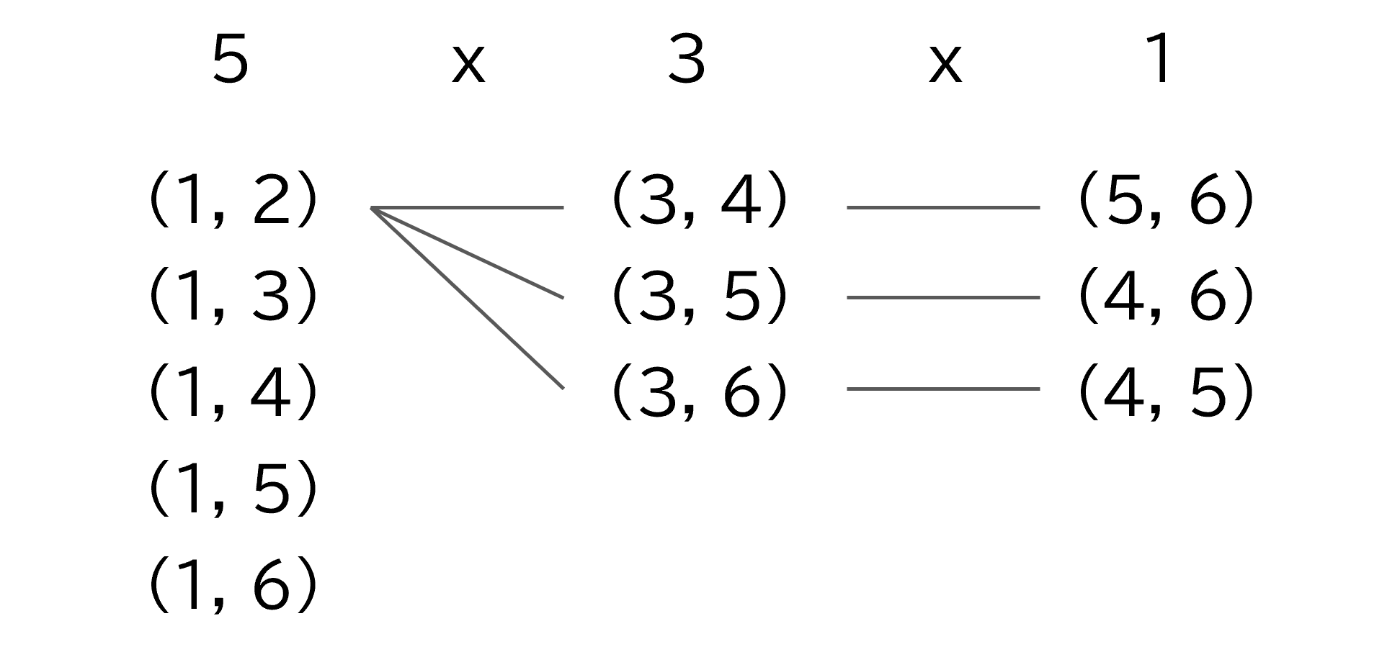
最大の16人の場合は $15\times13\times11\times....\times1=2027025$ となり、間に合いそうです。

次にどうやってその組み合わせを求めるかですが、「集合の最小値ととそのペアとなる要素を抽出する→集合からペアを削除する」という操作を繰り返し行うことで得られます。
以下に6人の場合で{(1,2), (3,4), (5,6)}を求める流れを図示しました。

集合から特定の要素を削除するには、set型の排他的論理和^が便利です。

排他的論理和.py

{1} ^ {1,2,3,4}
# {2,3,4}

具体的には、以下の操作を繰り返し行います。

# 6人いるときに「1人目とそのペア、および残り4人の集合」の組み合わせを全て出力します
N = 3
sets = set(range(1, N * 2+1))
i = min(sets)
sets ^= {i}
for j in sets:
    print(f"最小値：{i}, ペア：{j}, 集合：{sets ^ {j}}")
# 最小値：1, ペア：2, 集合：{3, 4, 5, 6}
# 最小値：1, ペア：3, 集合：{2, 4, 5, 6}
# 最小値：1, ペア：4, 集合：{2, 3, 5, 6}
# 最小値：1, ペア：5, 集合：{2, 3, 4, 6}
# 最小値：1, ペア：6, 集合：{2, 3, 4, 5}

同じ操作の繰り返しはDFSで行うことができます。

最後にBの値については、集合が空になったときのBの値をその組み合わせのBとして記録します。
Bの初期値は0とすると $0 \oplus x = x$ のため1回目のループで1組目の値がそのまま代入されるため問題ありません。

実装

再帰DFS

dfs関数の引数を深さと値の2つにすると書きやすいです。
本問ではsetsが全て揃った状態が深さの初期値で、setsの中身が空になったときの値が戻り値です。
なお、Pythonで提出するとTLEとなるため、PyPyで提出します。

d-recursion.py

import sys
sys.setrecursionlimit(10 ** 6)

N = int(input())
A = [list(map(int, input().split())) for _ in range(2 * N - 1)]

for i in range(2 * N - 1):
    A[i] = [-1] * (i + 1) + A[i]


def dfs(sets, value):
    ans = []
    if not sets:
        return value
    i = min(sets)
    sets ^= {i}
    for j in sets:
        ans.append(dfs(sets ^ {j}, value ^ A[i][j]))
    return max(ans)


sets = set(range(N * 2))

print(dfs(sets, 0))

スタックDFS

d-dfs-stack.py

# m193hさんのコードがとてもわかりやすく、ほとんど拝借させていただきました。
# https://zenn.dev/m193h/articles/20220123sun234653m193habc236

N = int(input())
A = [list(map(int, input().split())) for _ in range(2*N-1)]
for i in range(2*N-1):
    A[i] = [-1]*(i+1) + A[i]

ans = 0

stack = [(set(range(N * 2)), 0)]
while stack:
    sets, value = stack.pop()
    if not sets:
        ans = max(ans, value)
        continue
    # 集合の中の最小値を取り出し、削除します
    i = min(sets)
    sets ^= {i}
    for j in sets:
        # sets ^ {j}ではiのペアとなる要素を削除しています
        stack.append((sets ^ {j}, value ^ A[i][j]))

print(ans)