🐶

ABC231解説：本番でACできた問題＋1問（Python）

2022/02/05に公開

Python

A - Water Pressure

問題文のとおりに100で割り算をします。

a.py

D = int(input())

print(D/100)

B - Election

出現数を数えるにはCounterを使うと便利です。most_commonメソッドで最頻値を抽出できます。

b.py

from collections import Counter

N = int(input())
S = [input() for _ in range(N)]

print(Counter(S).most_common()[0][0])

C - Counting 2

NもQも $2 \times 10^{5}$ と大きいため、効率的な探索が必要です。
競プロ典型として、ソートしても答えが変わらない場合にはソートして考えるというものがあります。
そこでAの値をソートすると単調増加になるため、各生徒の身長のインデックスを二分探索で求る着想が得られます。

二分探索はbisectモジュールが便利です。

なお「身長が $x_j$ 以上の生徒は何人か」を求めるため、これは $x_j$ の値も含まれることからbisect_leftを用います。
仮に「身長が $x_j$ より大きいの生徒は何人か」の場合はbisect (bisect_right)を用います。

c.py

from bisect import bisect_left

N, Q = list(map(int, input().split()))
A = list(map(int, input().split()))
X = [int(input()) for _ in range(Q)]

A.sort()

for x in X:
    idx = bisect_left(A, x)
    print(N - idx)

D - Neighbors

一直線上に並ぶグラフのことをパスグラフと呼びます。

パスグラフの次数は2以下であることが知られています。
両端の次数は1で、途中のノードの次数は2です。

しかし、次数が2以下でも閉路がある場合にはリンググラフとなり、直線になりません。

そのため本問は閉路がなく、すべてのノードの次数が2以下であれば条件を満たすということになります。

閉路をもつか持たないかの判定はUnion Findを用いると簡潔に実装ができます。

Union Find: 閉路判定

Union Findは**要素aとbが同じグループに属するかを調べる(Find)こととaとbのグループを併合する(Union)**ことができるデータ構造です。

ここで、要素aとbが同じグループに属する判定は親となるノード（根）が一致しているかを見ることになります。
ここで根が一致している場合は、併合したときに閉路となるため、不適ということになります。

Union Find: parentsリスト

Union Findではparentsリスト（各要素の親要素の番号を格納するリスト）の値の更新が肝になります。
こちらのご説明が勉強になりました。
https://yaakublog.com/union_find

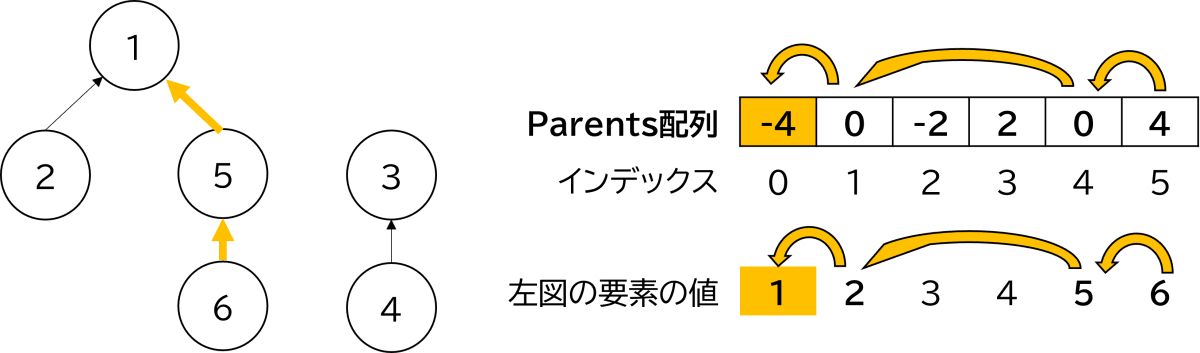
parentsリストにおいて負の数が親ノードを表すこと、ならびに正の数のインデックスを辿ると必ず負の親ノードに行き着くという点が重要です。

上記のご説明で、(2, 5)を結合したあとのParents配列を見てみます。
例えば6を基準に負の値となるまでインデックスを辿ると、(6->5->1)と確かに左図に対応していることがわかります。

d.py

import sys
sys.setrecursionlimit(10 ** 6)

N, M = list(map(int, input().split()))
AB = [tuple(map(int, input().split())) for _ in range(M)]

# parentsリスト
p = [-1] * N

def root(x):
    if p[x] < 0:
        return x
    p[x] = root(p[x]) # 経路圧縮
    return p[x]


def unite(x, y):
    x = root(x)
    y = root(y)
    if x == y:
        return
    p[x] += p[y]
    p[y] = x


degree = [0] * N

for i in range(M):
    a, b = AB[i]
    a -= 1
    b -= 1
    degree[a] += 1
    degree[b] += 1
    # 根が共通する場合にはUniteをすると閉路を形成してしまい、
    # 一直線上にならなくなるためNoと出力し終了します
    if root(a) == root(b):
        print("No")
        exit()
    # root(a)がroot(b)の親となるようにつなぎます
    unite(a, b)

if max(degree) <= 2:
    print("Yes")
else:
    print("No")