Zenn
🌊

Numpyで時系列データからフレーム系列を取得する

2022/12/11に公開
Python
Audio
numpy
時系列
tech

はじめに

時系列信号からフレーム系列を抽出するための関数とその使用例を紹介します．この関数はscipyの時系列用API（scipy.signal）で使われているプライベート関数 _fft_helperの一部を再利用しやすく切り出したものです．

背景

時系列信号を一定時間のフレームに分割して分析する処理は，音声の分野では主に短時間フーリエ変換などの際によく使われています．scipyなど多くのライブラリでは、この処理をAPIとして実装しています．

しかし，一般のセンサ信号処理においては，抽出したフレームに対してFFT以外の処理を行うことがあります．例えば，周波数領域以外に時間領域の特徴量をフレームごとに計算するなどです．このような場合，時間領域のフレーム系列が必要になりますが，scipyでは各フレームにFFTを施したスペクトログラムのみが提供されています．

そこで，本記事ではnumpyで複数チャネルの時系列信号から時間領域のフレーム系列を抽出するテクニックを紹介します．より具体的には、numpyのstride_tricks.as_strided()関数を用いてフレーム系列の抽出を行います．

実装

import numpy as np

def extract_frame_sequence(x: np.ndarray, nperseg: int, noverlap: int) -> np.ndarray:
    """
    時系列信号を一定時間のフレームに分割し、そのフレーム系列を取得する.
    This function splits a time series signal into fixed-length frames, and returns the resulting sequence of frames.

    Parameters
    ----------
    x : np.ndarray
        フレーム化する対象の時系列データ. The time series signal to be split into frames.
    nperseg : int
        1フレームに含まれるデータ数. The number of data points in each frame.
    noverlap : int
        フレーム間でオーバラップさせるデータ数. The number of data points to overlap between frames.

    Returns
    -------
    frames : np.ndarray
        抽出されたフレーム系列. A sequence of frames extracted from the input signal
    """
    step = nperseg - noverlap
    shape = x.shape[:-1] + ((x.shape[-1] - noverlap) // step, nperseg)
    strides = x.strides[:-1] + (step * x.strides[-1], x.strides[-1])
    frames = np.lib.stride_tricks.as_strided(x, shape=shape, strides=strides)
    return frames

extract_frame_sequence関数は時系列信号を固定長のフレームに分割するためのもので，この関数は3つの引数

  • 分割する時系列信号(x)
  • 各フレームのデータ点数(nperseg)
  • フレーム間で重複するデータ点数(noverlap)

をとり，xから抽出されたフレームのシーケンスを返します．

フレームを抽出するために，この関数はまずフレーム間のステップサイズ（nperseg - noverlap）を計算します．次に，このステップサイズを使ってnumpyライブラリのlib.stride_tricks.as_strided()関数を用いて入力信号xのviewを作成します．このviewにより，extract_frame_sequence関数はデータの不必要なコピーを作成することなく一連のフレームを効率的に抽出することができます．

使い方

1次元信号

extract_frame_sequence関数は，時系列信号を固定長のフレームに分割する方法を提供し，1次元および多次元の時系列データを扱うことができます．以下で使い方の例を紹介します．

例えば，1から15までの整数が並んだ時系列信号xがあり，それを窓長nperseg=4，フレーム間の重なり要素数noverlap=2のフレーム系列に分割したい場合を考えてみましょう．次のようにextract_frame_sequence関数を使うことができます．

import numpy as np
import extract_frame_sequence

x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])

frames_1 = extract_frame_sequence(x, nperseg=6, noverlap=2)
print(frames_1)
# [[ 1  2  3  4  5  6]
#  [ 5  6  7  8  9 10]
#  [ 9 10 11 12 13 14]]

frames_2 = extract_frame_sequence(x, nperseg=5, noverlap=3)
print(frames_2)
# [[ 1  2  3  4  5]
#  [ 3  4  5  6  7]
#  [ 5  6  7  8  9]
#  [ 7  8  9 10 11]
#  [ 9 10 11 12 13]
#  [11 12 13 14 15]]

2次元信号

2次元の時系列信号の場合でも，extract_frame_sequence関数を使用して信号の各チャネルからフレーム系列を抽出することができます．例えば，形状が(3, 5)の時系列信号xがあるとします．すなわち，チャンネル数が3で長さ5の時系列信号です．この信号の各行(チャネル)からフレーム系列を抽出するためにextract_frame_sequence関数を以下のように使用することができます．

x = np.array([[1, 2, 3, 4, 5],
              [6, 7, 8, 9, 10],
              [11, 12, 13, 14, 15]]) # 2次元配列

frames_3 = extract_frame_sequence(x, 3, 1)
print(frames_3.shape)
# (3, 2, 3)
print(frames_3)
# [[[ 1  2  3]
#   [ 3  4  5]]
#  [[ 6  7  8]
#   [ 8  9 10]]
#  [[11 12 13]
#   [13 14 15]]]

この場合，extract_frame_sequence関数はフレームの3次元配列を返し，各次元は入力信号の行，すなわち各チャネルに対応します．出力配列の次元は (3, 2, 3) となり，入力信号の3行からそれぞれ2フレームが含まれ，各フレームには3つの要素が含まれることが分かります．

3次元信号

3次元の信号とは例えば下図のようなものを言います．IR + Green + IMUで合計16チャネルあり，信号のながさをNとすると各チャネルのデータは (4, N)の形状になっています．よって，全体としてデータの形状が (16, 4, N)な信号となります．
fig
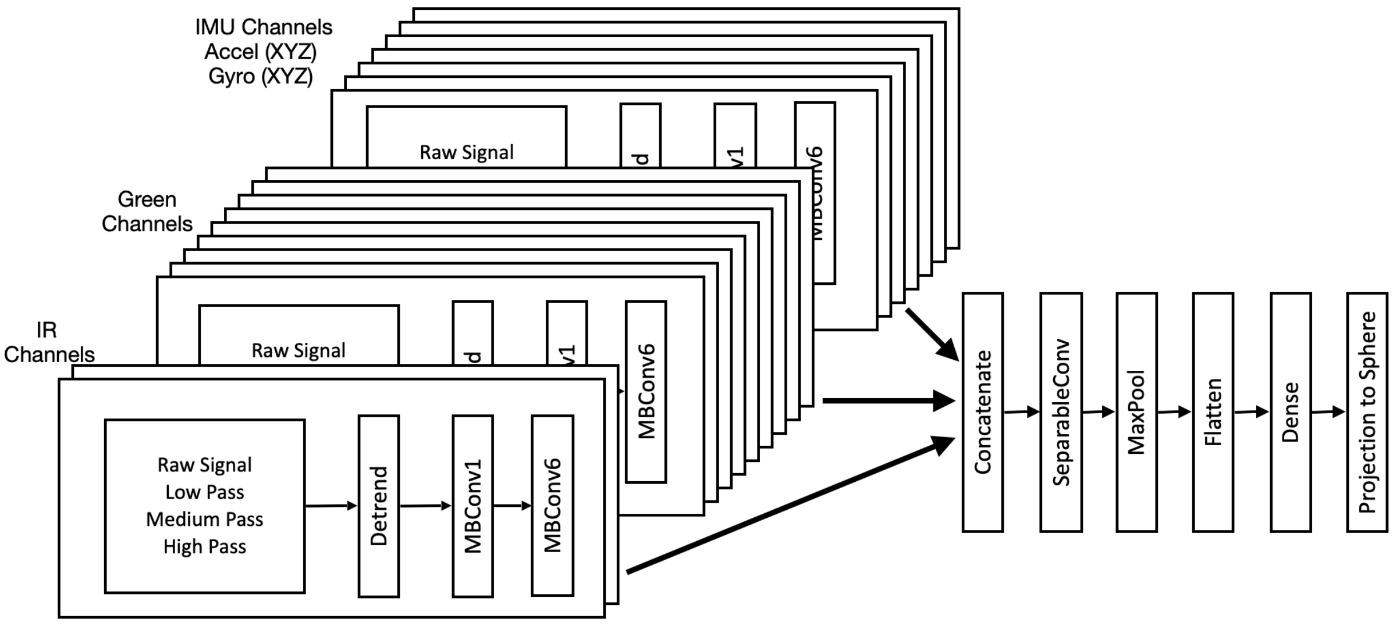
Fusion-Id: A Photoplethysmography and Motion Sensor Fusion Biometric Authenticator With Few-Shot on-Boardingより引用
N=10場合，nperseg=3，noverlap=2のフレーム系列を抽出するためにextract_frame_sequence関数を以下のように使用することができます．

x = np.arange(640).reshape((16,4,10))

frames = extract_frame_sequence(x, 3, 2)
print(frames.shape)
# (16, 4, 8, 3)

# IRチャネル/LowPassのフレーム系列にアクセスしたい場合
print(frames[0, 1,:,:]) 
# [[10 11 12]
#  [11 12 13]
#  [12 13 14]
#  [13 14 15]
#  [14 15 16]
#  [15 16 17]
#  [16 17 18]
#  [17 18 19]]

この場合，extract_frame_sequence関数はフレームの4次元配列を返し，各次元は(チャネル, チャネルの行, フレーム, チャネルの列)に対応します．出力配列の次元は (16, 4, 8, 3) となり，各チャネル/行は長さ3のフレームを8個持っていることが分かります．

解説

ステップ数の計算

step = nperseg - noverlap

フレーム間のステップサイズを nperseg - noverlap として計算しています。ただし，

  • nperseg: 各フレーム内のデータ数を指定する値．int型．
  • noverlap: フレーム間でオーバーラップするデータ数を指定する値．int型．

です．

フレーム系列の形状を計算

shape = x.shape[:-1] + ((x.shape[-1] - noverlap) // step, nperseg)

結果として得られるフレームの ndarray の形状を計算します．x.shape[-1] - noverlap) // stepが少し理解しづらいので具体例を使って説明します．例として，長さ10の1次元時系列信号を考えてみましょう．npersegを3，noverlapを1とすると次のように説明できます．まず，この関数では少なくとも1つのフレームは抽出する必要があるので先頭のフレームを取り出します．残りの要素は10個となり，これをstep幅2で分割すると 7 // 2 = 3 となります．ただし，無効な値をフレームに含まないように切り捨て除算をしています．先頭の1つのフレームと残りの時系列に対するフレームの個数を足すと 1 + 3 = 4 となり，最終的に必要なフレーム数は4つと求まりました．
fig2

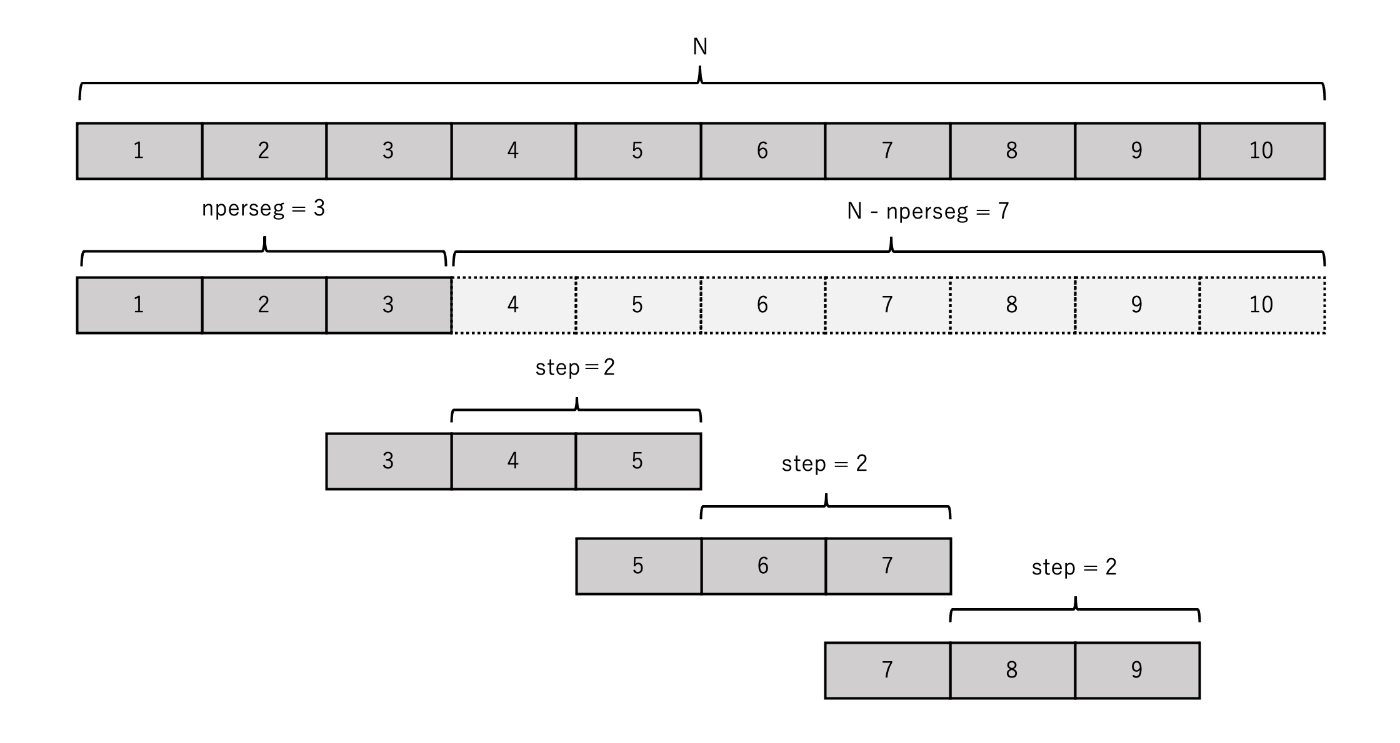
以上の話を一般化してみましょう．時系列長をNとすると，全体から先頭のフレームを除いた時の要素数はN - npersegになります．これをstepで切り捨て除算した(N-nperseg)//stepが残りの要素から抽出されるフレーム数です．よって，抽出されるフレームの総数は(N-nperseg)//step + 1で，これは

\begin{aligned} (\rm{N}-\rm{nperseg})//\rm{step} + 1 &= (\rm{N} - \rm{nperseg} + \rm{step})//\rm{step} \\ &= (\rm{N} - \rm{nperseg} + \rm{nperseg} - \rm{noverlap})//\rm{step}\\ &= (\rm{N}-\rm{noverlap})//\rm{step} \end{aligned}

と書き換えられることがわかります．以上より，結果として得られるフレーム系列の形状は(フレーム数，各フレームに含まれるデータ数)=((x.shape[-1] - noverlap) // step, nperseg)となります．

Strideの計算

strides = x.strides[:-1] + (step * x.strides[-1], x.strides[-1])

Strideでは，最終的に抽出されるフレーム系列において，ある次元に沿って次の要素に移動するためにメモリ上でスキップすべきbyte数です．例えば，フレーム系列の形状が(4, 3)で要素がfloat64型の場合，データアクセスのindexが2次元目(横方向)に沿って1増えるとメモリ領域が8byteずれ，2次元目(縦方向)に沿ってindexが1増えるとメモリ領域は8 × 3 = 24byteずれることになります．すなわちこの場合のStrideは(24,8)となります．また，numpyの配列操作に関する詳細な説明はこちらの記事が参考になると思います．

フレーム系列への分割

frames = np.lib.stride_tricks.as_strided(x, shape=shape, strides=strides)

np.lib.stride_tricks.as_stridedを使用して，計算された形状shapeとstridesを持つフレームのndarrayのviewを生成しています．

おまけ

おまけとして，短時間フーリエ変換(STFT)をfor文を使って実装した場合と，scipy.stftを使った場合，extract_frame_sequence関数を使った場合で比較してみてみます．

短時間フーリエ変換

全体の長さが10000の次のような時系列データを考えてみましょう．

対象となる信号
import numpy as np

N = 10000
t = np.linspace(0, 10, N)
x = np.sin(64*np.pi*t) + np.sin(128*np.pi*t) + np.random.normal(loc=0, scale=1, size=t.shape)

このデータをフレームサイズ512，オーバラップ数128でSTFTしてみます．scipy.stftを使うと次のように実装できます．

scipy.stftを利用したSTFTの計算
from scipy import signal

nperseg=512
noverlap=128
f, t, Zxx = signal.stft(x,nperseg=nperseg, noverlap=noverlap,padded=False,boundary=None)

便利ですね．．．
一方で，extract_frame_sequenceを利用したSTFTは次のように実装できます．

extract_frame_sequenceを利用したSTFTの計算
from frame_sequence import extract_frame_sequence
from scipy.fft import rfft, rfftfreq

def stft(x, nperseg, noverlap):
    frames = extract_frame_sequence(x, nperseg, noverlap)
    han = signal.get_window("hann", nperseg)
    scale = 1.0 / han.sum()  # 窓関数補正係数
    return rfft(frames * han) * scale
    
result = stft(x, nperseg, noverlap)

print(result.T.shape == Zxx.shape) 
# True
print(np.allclose(result.T,Zxx)) 
# True

今回はextract_frame_sequenceが正しく動いていることを確かめたいので窓関数やfft関数はscipyのものを利用しました．np.allcloseは2つの配列が誤差の範囲で等しいかを判定するための関数です．この場合，extract_frame_sequence関数を利用して取得したスペクトログラムがscipy.stftを利用して取得したものと絶対誤差が1e-08以下かつ相対誤差も1e-05以下で一致していることが分かります．下図のように可視化して比べてみても一致していることが分かりますね．


もしextract_frame_sequence関数を使わずに単純なfor文で実装すると次のようになります．

for文でフレーム抽出を行うSTFTの計算
def stft(x, nperseg, noverlap):
    step = nperseg - noverlap
    T = (x.shape[-1] - noverlap) // step
    han = signal.get_window("hann", nperseg)
    scale = 1.0 / han.sum()  # 窓関数補正係数
    spec = np.zeros((T, nperseg//2+1), dtype="complex")
    for t in range(T):
        fft_data = rfft(x[t*step : t*step+nperseg] * han) * scale
        spec[t,:]=fft_data
    
    return spec
    
    
result = stft(x, nperseg, noverlap)
print(result.T.shape == Zxx.shape) 
# True
print(np.allclose(result.T,Zxx)) 
# True

こちらの結果もscipy.stftの出力と一致しました．

各フレームの特徴量を計算する

次に，形状が(16, 4, 1000)の3次元信号からフレームごとに時間領域の特徴量を計算してみましょう．まずは，次のようにサンプル信号を生成します．

信号の生成
N = 10000 # 10000 samples
t = np.linspace(0, 100, N) # 100 seconds

x = np.zeros((16,4,N)) 
for i in range(16):
　　　　for j in range(4):
    x[i,j,:] = np.sin((i+1)*np.pi*t) + np.random.normal(loc=0, scale=1, size=t.shape)

この信号が具体的にどういったものなのかは無視して配列の形状に着目してみていきましょう．

フレームサイズ512，オーバーラップ数128でフレーム系列を取得します．extract_frame_sequence関数を使うと次のように書けます．

フレーム系列の取得
# extract frames
nperseg=512
noverlap=128
frames = extract_frame_sequence(x, nperseg, noverlap)

print(frames.shape)
# (16, 4, 25, 512)

各チャネル/行について長さ512のフレームを25個持っていることが分かります．このフレーム系列の平均と標準偏差を計算してみましょう．

各フレームの平均と標準偏差を計算する
# calculate the mean of each frame
mymean = np.mean(frames, axis=3)
# calculate the standard deviation of each frame
mystd = np.std(frames, axis=3)

print(mymean.shape)
print(mystd.shape) 
# (16, 4, 25)
# (16, 4, 25)

フレーム内の512個の要素に対して平均と標準偏差を計算するので，配列の形状は(16, 4, 25, 512)→(16, 4, 25)と変化します．

次に，自分で定義した特徴量を計算する関数を用いて各フレームに対して計算してみましょう．ここでは，例としてMYOPと呼ばれる特徴量を計算してみます．

特徴量MYOPを計算する関数
def get_myop(frame, threshold):
    N = frame.shape[0]
    MYOP = np.sum(frame >= threshold) / N
    return MYOP

get_myop関数は1次元配列と閾値を引数にとりスカラー値のMYOPを返します．このような1次元の配列を引数とする関数を多次元の配列に適用したい場合はnp.apply_along_axisを利用することで次のように書けます．

myop = np.apply_along_axis(my_feature, axis=3, arr=frames, threshold=0.5)
print(myop.shape)
# (16, 4, 25)

各フレームに対してスカラーの特徴量を計算しているので平均や標準偏差と同じように配列の形状が(16, 4, 25)になっています．これで正しく各フレームに対して特徴量を計算できていることが確認できました[1]．

まとめ

この記事では，時系列信号を固定長のフレームに分割するためのextract_frame_sequence関数とその使用例を紹介しました．この関数は，scipyの時系列用APIであるscipy.signalで使用されているプライベート関数_fft_helperの一部を再利用しやすく切り出したものです．これにより，複数チャネルの時系列信号から時間領域のフレーム系列を抽出することができました．

脚注

  1. あくまで形状のみの確認なので実際に使うときは特徴量を計算する関数が正しく動作しているかテストすることを推奨します．サンプルコードはテストしやすいように1次元配列を引数に取っています． ↩︎

Discussion