😺
claude codeにフラクタル図形書かせてみた

2025/09/11に公開
今回はclaude codeを使ってフラクタル図形を作らせてみました。claude codeをはじめ生成AIはどこまでできる能力があるのかを測るためのシリーズになります。前回は立方体をターミナルでぐるぐる回すものをやりましたが、それの第二弾ですね。
https://zenn.dev/akasan/articles/11fed840eedaa7
※ バタバタしていて、コードの解説まではできません。次回以降行けるタイミングでさせてもらいます

 フラクタル図形とは？Wikipediaによると
図形の部分と全体が自己相似（再帰）になっているものなどをいう
ということです。あるAから一部Bを切り取った時にAとBが同じようなものになっているという感じでしょうか。詳しくはWikipediaをぜひ調べてください。
https://ja.wikipedia.org/wiki/フラクタル

 早速結果共有まずは以下のように環境構築しました。
uv init fractal_python -p 3.12
cd fractal_python
ここでclaudeには以下の指示だけ与えました。
pythonを使って、2次元のフラクタル図形を段階的に生成してアニメーションとして保存するコードを書いて。uvを使って
とてつもなく雑な指示ですが、これだけで作ってくれましたw。
実際に生成されたコードは以下になります。
fractal_animation.py
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.patches import Polygon
from PIL import Image
import os

def sierpinski_triangle(order, ax, vertices=None):
    if vertices is None:
        vertices = np.array([[0, 0], [1, 0], [0.5, np.sqrt(3)/2]])
    
    triangles = []
    
    def divide_triangle(v, depth):
        if depth == 0:
            triangles.append(v)
        else:
            mid1 = (v[0] + v[1]) / 2
            mid2 = (v[1] + v[2]) / 2
            mid3 = (v[2] + v[0]) / 2
            
            divide_triangle(np.array([v[0], mid1, mid3]), depth - 1)
            divide_triangle(np.array([mid1, v[1], mid2]), depth - 1)
            divide_triangle(np.array([mid3, mid2, v[2]]), depth - 1)
    
    divide_triangle(vertices, order)
    
    for tri in triangles:
        triangle = Polygon(tri, closed=True, facecolor='blue', edgecolor='blue')
        ax.add_patch(triangle)

def koch_snowflake(order, ax):
    def koch_line(start, end, depth):
        if depth == 0:
            return [start, end]
        
        vec = end - start
        p1 = start + vec / 3
        p2 = start + 2 * vec / 3
        
        angle = np.pi / 3
        rotation = np.array([[np.cos(angle), -np.sin(angle)],
                           [np.sin(angle), np.cos(angle)]])
        p3 = p1 + rotation @ (p2 - p1)
        
        points = []
        points.extend(koch_line(start, p1, depth - 1)[:-1])
        points.extend(koch_line(p1, p3, depth - 1)[:-1])
        points.extend(koch_line(p3, p2, depth - 1)[:-1])
        points.extend(koch_line(p2, end, depth - 1))
        
        return points
    
    triangle = np.array([[0, 0], [1, 0], [0.5, np.sqrt(3)/2], [0, 0]])
    
    all_points = []
    for i in range(3):
        points = koch_line(triangle[i], triangle[i+1], order)
        all_points.extend(points[:-1])
    
    all_points = np.array(all_points)
    ax.fill(all_points[:, 0], all_points[:, 1], 'cyan', edgecolor='blue', linewidth=0.5)

def mandelbrot_set(xmin, xmax, ymin, ymax, width, height, max_iter):
    x = np.linspace(xmin, xmax, width)
    y = np.linspace(ymin, ymax, height)
    X, Y = np.meshgrid(x, y)
    C = X + 1j * Y
    
    Z = np.zeros_like(C)
    M = np.zeros(C.shape)
    
    for i in range(max_iter):
        mask = np.abs(Z) <= 2
        Z[mask] = Z[mask]**2 + C[mask]
        M[mask] = i
    
    return M

def create_fractal_animation(fractal_type='sierpinski', max_order=7, filename='fractal_animation.gif'):
    fig, ax = plt.subplots(figsize=(8, 8))
    
    def update(frame):
        ax.clear()
        ax.set_aspect('equal')
        ax.axis('off')
        
        if fractal_type == 'sierpinski':
            ax.set_xlim(-0.1, 1.1)
            ax.set_ylim(-0.1, 1)
            sierpinski_triangle(frame, ax)
            ax.set_title(f'Sierpinski Triangle - Order {frame}', fontsize=16)
            
        elif fractal_type == 'koch':
            ax.set_xlim(-0.2, 1.2)
            ax.set_ylim(-0.2, 1.2)
            koch_snowflake(frame, ax)
            ax.set_title(f'Koch Snowflake - Order {frame}', fontsize=16)
            
        elif fractal_type == 'mandelbrot':
            zoom_factor = 0.8 ** frame
            xmin, xmax = -2 * zoom_factor, 1 * zoom_factor
            ymin, ymax = -1.5 * zoom_factor, 1.5 * zoom_factor
            
            M = mandelbrot_set(xmin, xmax, ymin, ymax, 400, 400, 50 + frame * 20)
            ax.imshow(M, extent=[xmin, xmax, ymin, ymax], cmap='hot', origin='lower')
            ax.set_title(f'Mandelbrot Set - Zoom Level {frame}', fontsize=16)
    
    frames = max_order if fractal_type != 'mandelbrot' else 10
    ani = animation.FuncAnimation(fig, update, frames=range(frames), interval=500, repeat=True)
    
    ani.save(filename, writer='pillow', fps=2)
    plt.close()
    
    print(f"Animation saved as {filename}")

def create_all_fractals():
    os.makedirs('claude/log', exist_ok=True)
    
    print("Generating Sierpinski Triangle animation...")
    create_fractal_animation('sierpinski', 10, 'claude/log/sierpinski_triangle.gif')
    
    print("Generating Koch Snowflake animation...")
    create_fractal_animation('koch', 10, 'claude/log/koch_snowflake.gif')
    
    print("Generating Mandelbrot Set zoom animation...")
    create_fractal_animation('mandelbrot', filename='claude/log/mandelbrot_zoom.gif')
    
    print("\nAll animations have been generated in ./claude/log/")

if __name__ == "__main__":
    create_all_fractals()
結果をみると3種類のフラクタル図形を作成していることがわかります。それぞれ以下のWikipediaに紹介されています。どれも有名なのでみたことある方もいるのではないでしょうか。コードの解説は今回は対象としないですが再帰処理がどれも入っており、フラクタル図形を作る上では基本要素なのでちゃんと作られてるなと感心しました。
https://ja.wikipedia.org/wiki/シェルピンスキーのギャスケット
https://ja.wikipedia.org/wiki/コッホ曲線
https://ja.wikipedia.org/wiki/マンデルブロ集合
それでは実行してみます。
uv run fractal_animation.py
実行が完了すると以下のような結果がそれぞれ表示されます。




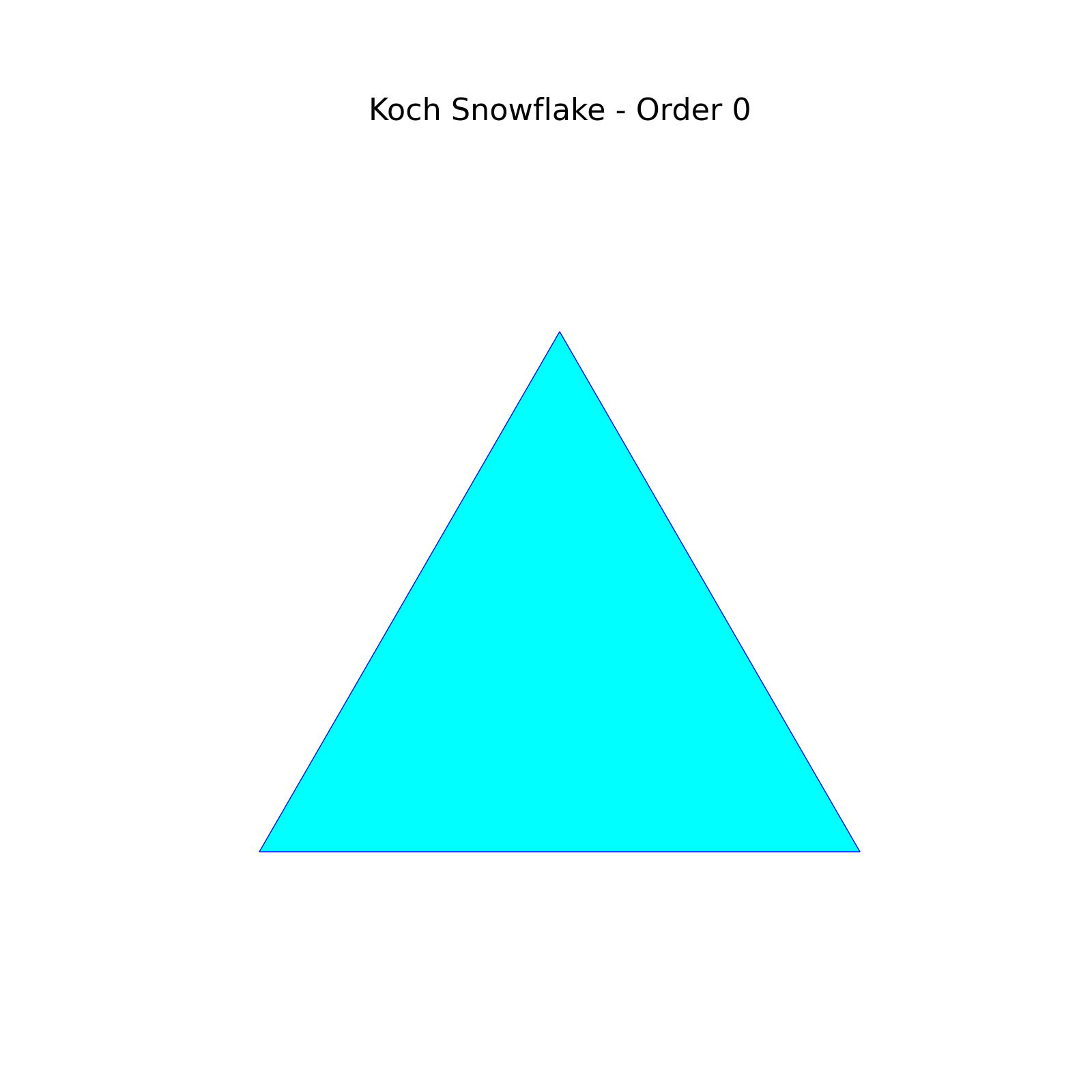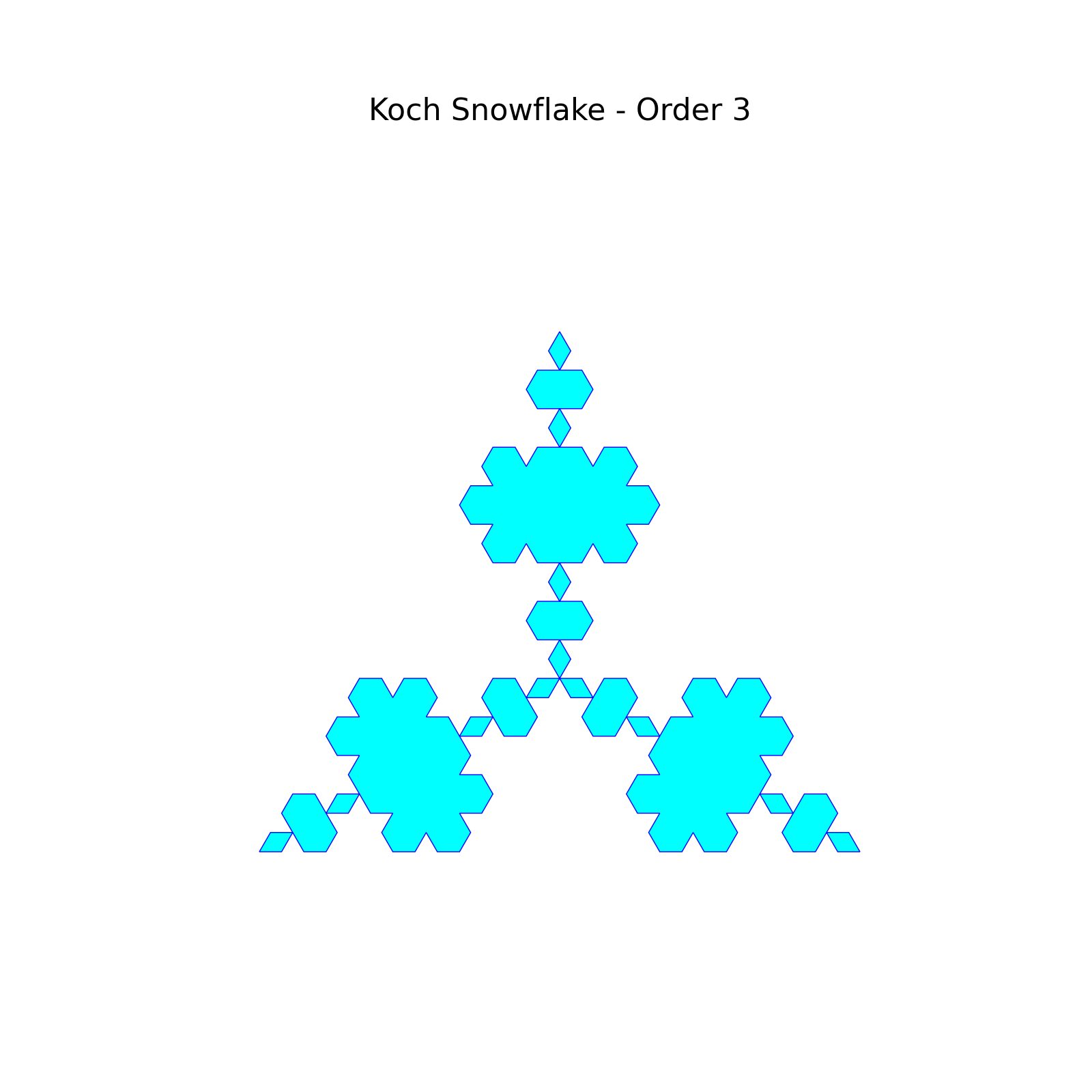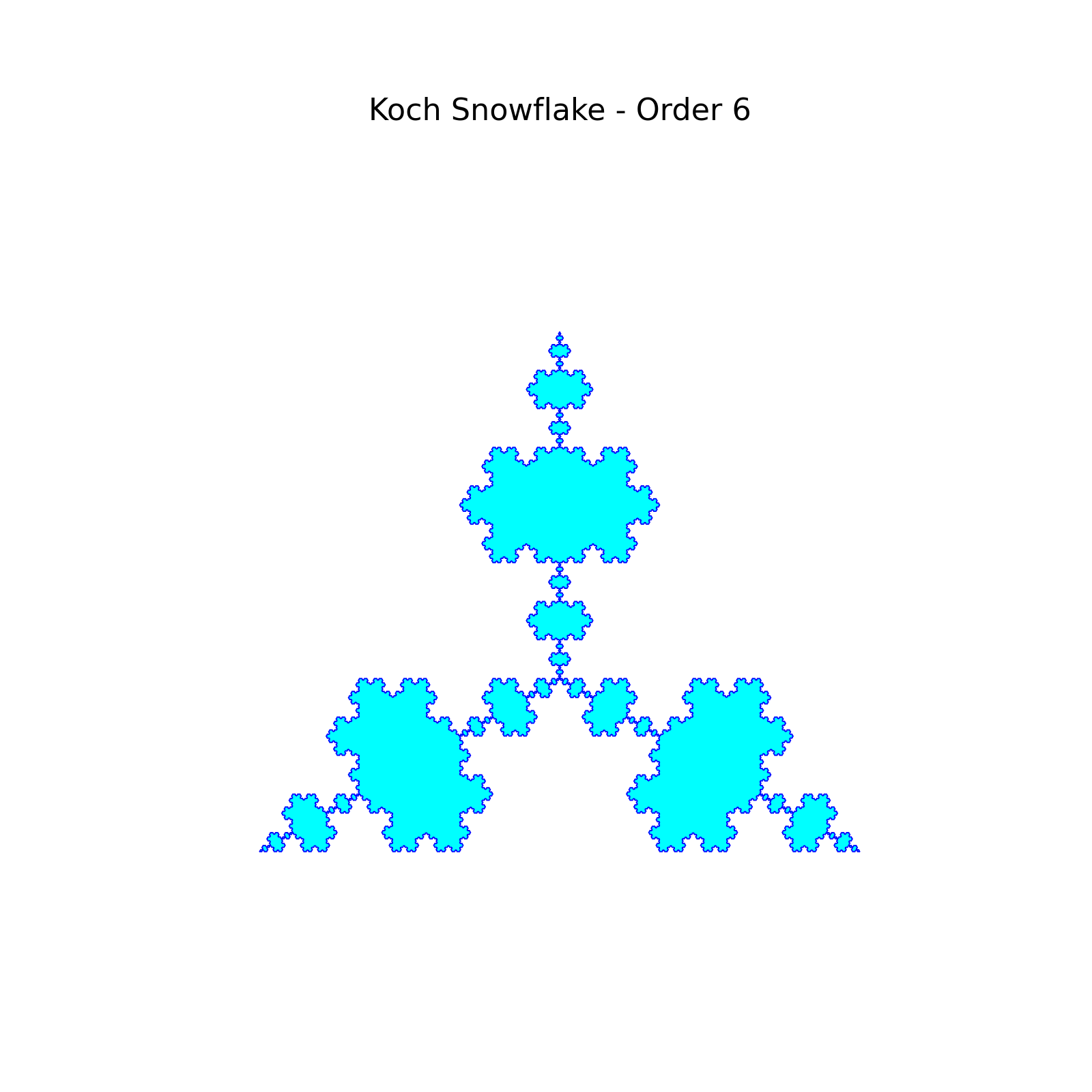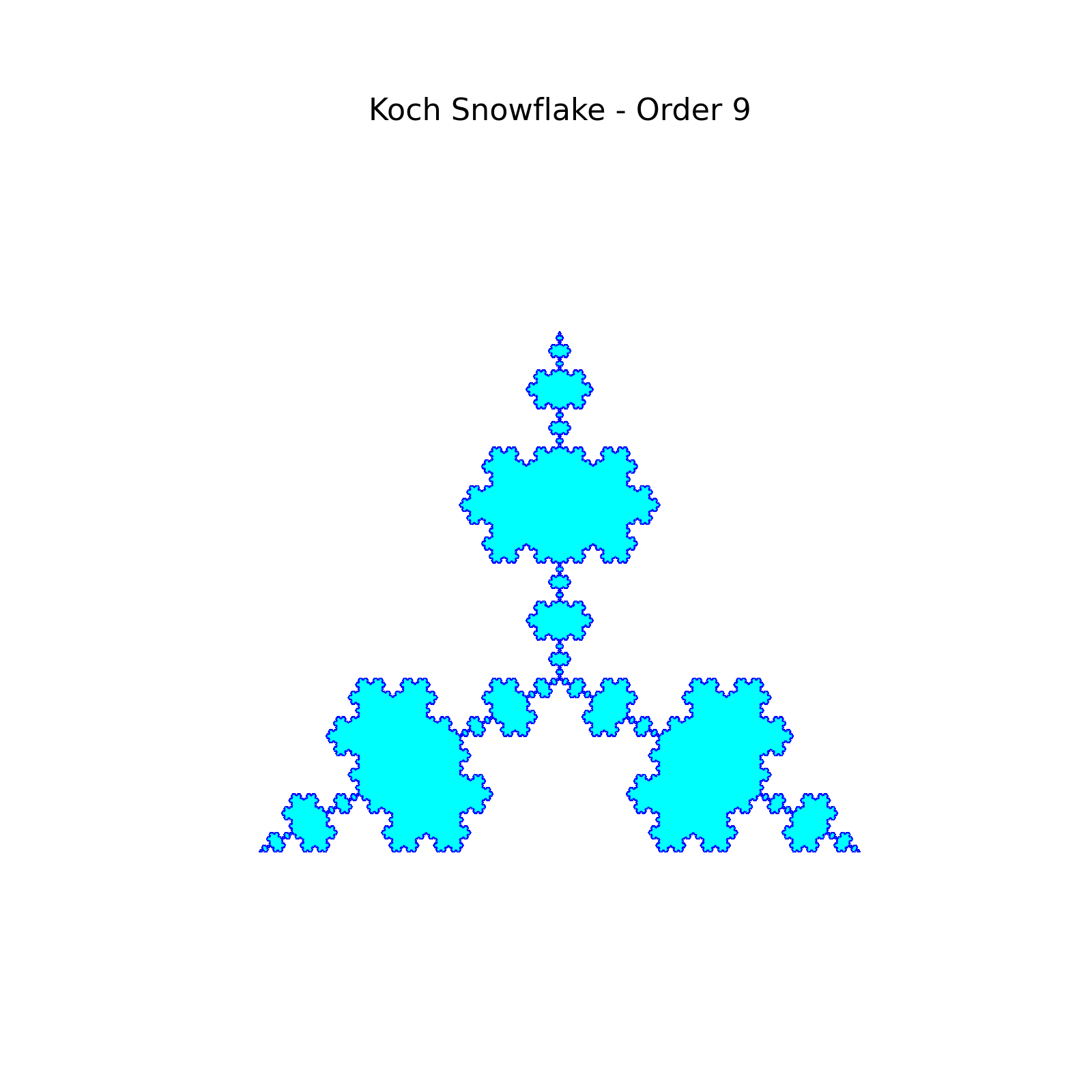
最後の一つはズームをするという結果になっていて全体像は見えなくなっていますが、どれも実装としては問題なくできていそうです。

 まとめ今回はclaude codeにフラクタル図形を作らせてみました。最初は何回かやりとりしないと失敗するだろうなと思っていましたが、やってみると意外と一発でいけてお！となりました。フラクタル図形を普段作成する必要がある人はほとんどいないと思いますが、ご興味があればぜひ実装してみてください！
フラクタル図形とは？

早速結果共有

まとめ

Discussion
