MAU・DAU・ヘビーユーザ数の関係性を考察してみた

問題設定

あるサービスの月間のユーザ数(= MAU)を $N$ 、1日のユーザ数(= DAU)を $M$ とする。
このサービスを月間20日以上利用しているユーザ数（= ヘビーユーザ数）は？

という問題を考察したのでメモ。

考察

MAU に含まれるユーザで1ヶ月（30日としておく）のうち $x$ 日利用する人の割合を $P(x)$ とおく。
求めたいのは $\sum_{x=20}^{30} NP(x)$ である。

DAU に含まれるユーザで1ヶ月のうち $x$ 日利用する人の数は $NP(x) \times \frac{x}{30}$ 人。
よって DAU は

$$M = \sum_{x=1}^{30} NP(x) \times \frac{x}{30}$$

と表せて、ここから1ユーザあたりの利用日数の期待値が

$$E[x] = \sum_{x=1}^{30} xP(x) = 30\frac{M}{N} = 30R$$

となることがわかる（ただし $R = \frac{M}{N}$ とおいた）。
これ割と非自明な結果だと思ったんですが自明ですかね🤔
（例えば DAU と MAU の比率が 1:4 だったら1ユーザが1ヶ月に利用する期間の期待値が1週間ということ）

というわけで、 DAU と MAU の値からは分布の期待値しか決まらないことがわかったので、ヘビーユーザの数を推定するには分布を仮定する必要がある。
簡単のために指数分布 $P(x)=\lambda e^{-\lambda x}$ を仮定しよう。

指数分布の期待値は $E[x]=\frac{1}{\lambda}$ だから $\lambda = \frac{1}{30R}$ となる。
20日以上利用しているユーザ数は

$$\sum_{x=20}^{30} NP(x) \sim \int_{20}^{\infty} NP(x) dx = \int_{20}^{\infty} N \lambda e^{- \lambda x} dx = N \bigl[ -e^{-\frac{x}{30R}} \bigr]_{20}^{\infty} = Ne^{-\frac{2}{3R}}$$

となった。

検証

さて、当社サービス（A~G）の過去30日の $R$ (= DAU / MAU) と $H$ (= ヘビーユーザ数 / MAU) を実際に見てみると、以下の様になっていた。

サービス	R	H
A	0.5615171138	0.559666975
B	0.4487651549	0.3297709924
C	0.284519828	0.1698518872
D	0.2378303199	0.09469170144
E	0.2018749334	0.07414509428
F	0.1734296832	0.08282379099
G	0.08352623457	0.01080246914

ログイン日数を指数分布で仮定した場合は $H = e^{-\frac{2}{3R}}$ なのでそれと重ねてプロットすると以下の様になった。

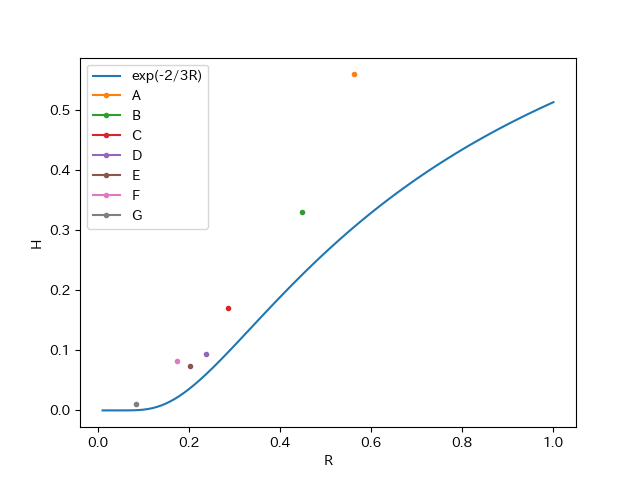
そもそも MAU に占めるヘビーユーザの割合が高い場合は指数分布の仮定が適切ではないので、 $H$ が大きいところでは大きくずれ、小さいところは比較的近くなっている様子が伺える。
これを見るとサービス F は $R$ の割には $H$ が大きい、と言えそう？

実際ログイン日数の分布を見ても $H$ が小さい E や G は指数分布に近く、 A や B は程遠そうな雰囲気があった。

そもそも指数分布はポアソン過程（あるイベントが一定確率で発生する）から導かれる分布だから、指数分布に近いということは「何かそれが必要なイベントが一定確率で発生して利用する」サービスだということになる。サービス E や G は確かにそういう性質のサービスだなあという感想だし、 F はちょっと系統が違うサービスではあった。