👻

Standard ML の機能だけ使って幽霊型で部分型付けする (2)

2022/11/13に公開

OCaml

phantomtypes

typelevelprogrammi

tech

「Standard ML の機能だけ使って幽霊型で部分型付けする (1)」では Standard ML の言語機能だけで部分型付けを実現する方法を紹介しましたが、有界全称型（forall 'a <: t. 'a -> 'a のような型）を実現するために色々な制限が付いていました。今回紹介する方法も Standard ML の言語機能だけで部分型付けを実現しますが、有界全称型の実現を完全に諦めて、共変性と反変性の実現に重点を置いています。部分型について知らない人は「幽霊型による部分型付けの紹介」を読むと良いでしょう。

概要

この方法でのモチベーションは、「有界全称型は諦めて共変性と反変性をできるだけ再現すること」にあります。例えば、int <: float という部分型関係があるとき、

int 型の値と float 型の値を同じリストに入れると float list の型が付く
float -> int <: int -> float という部分型関係が成り立つ

というようなことを実現することを目指します。

エンコードの例

定義を見る前に、前回と同様 int <: float という部分型関係を導入したサンプルプログラムを見てみます。

module M : sig
  type w (* 幽霊型 *)
  type z (* 幽霊型 *)
  type 'a t (* 'a は幽霊型変数 *)
  val int : int -> 'a t
  val float : float -> w t
  val (+) : 'a t -> 'a t -> w t  (* : float -> float -> float *)
  val (mod) : z t -> z t -> 'a t (* : int -> int -> int *)
  val int_of_float : 'a t -> 'b t (* : float -> int *)
  val float_of_int : z t -> w t   (* : int -> float *)
end = struct
  type w
  type z
  type 'a t = Int of int | Float of float
  let int x = Int x
  let float x = Float x
  let (+) x y = match x, y with
    | Int x, Int y -> Int (x + y)
    | Int x, Float y -> Float (float_of_int x +. y)
    | Float x, Int y -> Float (x +. float_of_int y)
    | Float x, Float y -> Float (x +. y)
  let (mod) x y = match x, y with
    | Int x, Int y -> Int (x mod y)
    | _ -> assert false (* float が渡されないことを幽霊型が保証する *)
  let int_of_float = function
    | Float x -> Int (Pervasives.int_of_float x)
    | Int x -> Int x
  let float_of_int = function
    | Float _ -> assert false (* float が渡されないことを幽霊型が保証する *)
    | Int x -> Float (Pervasives.float_of_int x)
end

ポイントは

int は共変な位置では 'a t、反変な位置では、z t とエンコードされている
float は共変な位置では w t、反変な位置では、'a t とエンコードされている

ということです。例えば、int と float の値を同じリストに入れると、

# open M;;
# [int 42; float 123.];;
- : w t list = [<abstr>; <abstr>]

と float list に対応する型 w t が付きます。また、float -> int <: int -> float なので、int_of_float と float_of_int を同じリストに入れることもできるはずです。

# [int_of_float; float_of_int];;
- : (z t -> w t) list = [<fun>; <fun>]

ちゃんと、int -> float に対応する型 z t -> w t が付きましたね。部分型付けの共変性も反変性もしっかりと再現できていることが確認できました。

この方法の制限

ちなみに、以前の記事では + は forall 'a <: float. 'a -> 'a -> 'a という型をエンコードした型でしたが、今回は有界全称型が使えないので、float -> float -> float をエンコードした型になっています。違いは int 型の値を両方のオペランドに渡した時、前者では int、後者では float が戻り値型になります。

一般的な部分型関係のエンコード

int <: float の具体例が理解できたので、もっと一般的な部分型付けをエンコードする方法について、見てみましょう。
この記事での定義は「Standard ML の機能だけ使って幽霊型で部分型付けする (1)」で紹介されている Phantom Types and Subtyping [Fluet and Pucella, JFP 2006] をベースにしています。とりあえず、基本型上の部分型関係と powerset lattice が得られたものとして、話を進めていきます。

基本型のエンコード

共変な位置でのエンコーディング $\langle X\rangle_+$ と反変な位置でのエンコーディング $\langle X\rangle_-$ をそれぞれ、次のように定義します。

$\langle X\rangle_+ = t_1 * \cdots * t_n$ where $t_i$ is
- w if $s_i\in X$
- $\texttt{'a}_i$ otherwise
$\langle X\rangle_- = t_1 * \cdots * t_n$ where $t_i$ is
- $\texttt{'a}_i$ if $s_i\in X$
- z otherwise

ただし $\texttt{'a}_i$ はフレッシュな型変数です（他の型変数と重複しない型変数）。

例えば、int <: float において int、float をそれぞれ空集合と $\{1\}$ に対応させた場合、

型	at covariant position	at contravariant position
`float`	`w`	`'a`
`int`	`'a`	`z`

となります。もう少し複雑な例として、次のハッセ図のような部分型関係を考えてみます。

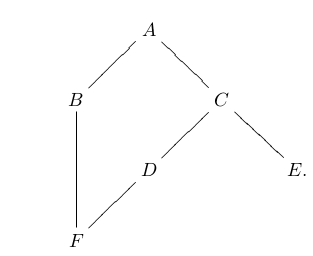
Subtyping Hierarchy

基本型 A〜F について、A :> B :> F、A :> C :> D :> F、C :> E であり、 $A=\{1,2,3,4\},B=\{1,2\},C=\{2,3,4\},D=\{2,3\},E=\{3\},F=\{2\}$ のように対応させると、

型	at covariant position	at contravariant position
A	`w * w * w * w`	`'a1 * 'a2 * 'a3 * 'a4`
B	`w * w * 'a3 * 'a4`	`'a1 * 'a2 * z * z`
C	`w * 'a2 * w * w`	`'a1 * z * 'a3 * 'a4`
D	`w * 'a2 * w * 'a4`	`'a1 * z * 'a3 * z`
E	`'a1 * 'a2 * 'a3 * w`	`z * z * z * 'a4`
F	`w * 'a2 * 'a3 * 'a4`	`'a1 * z * z * z`

となります。

関数型のエンコード

関数型の中に現れる基本型は、共変な位置なら $\langle X\rangle_+$ 反変な位置なら $\langle X\rangle_-$ でエンコードします。

例えば、A -> B -> C という関数型だと A と B は反変で、C は共変なので

('a1 * 'a2 * 'a3 * 'a4) t -> ('a5 * 'a6 * z * z) t -> (w * 'a7 * w * w) t

となり、(A -> B) -> C だと A、C は共変で B のみ反変なので、

((w * w * w * w) t -> ('a1 * 'a2 * z * z) t) -> (w * 'a7 * w * w) t