💨

three.js MathUtils全関数まとめ

2023/04/13に公開

JavaScript

Three.js

math

tech

趣旨

three.jsには、諸々の計算用の関数をまとめたMathUtilsが存在する。

これをなるべく理解しやすい形にまとめてみた。

MathUtilのソースコードはこちら

内容

clamp

値value、最小値min、最大値maxを渡す。
valueがminからmaxの間ならばvalueを返す
valueがminより小さければminを返す
valueがmaxより大きければmaxを返す

const val = 3;
THREE.MathUtils.clamp(3, 5, 10); //=> 5

★GLSLでよく出てくるので重要。

degToRad

度数法の角度を弧度法の角度（ラジアン）に変換。
例は略

euclideanModulo

余りを求める際、余りが負の値にならないように結果を返す関数。
例えば -5 % 2 はJSでは-1になる（2 * -2 - 1）
euclidianModuloを使うと、1が返る（2 * -3 + 1）
数学的にはeuclidianModuloが正しいみたい

この記事で解説してくれている人がいる

回転の制御で使うことがあるらしい。

THREE.MathUtils.euclideanModulo(-5, 2); //=>1

generateUUID

UUIDをgenerateする関数。

isPowerOfTwo

二人で力を合わせればなんとかなる
ではなく、渡した値がある数の2乗であるかどうかを返す。

THREE.MathUtils.isPowerOfTwo(56); //false
THREE.MathUtils.isPowerOfTwo(64); //true

inverseLerp

開始値x, 終了値y, 値valueを渡す。
xからyの範囲におけるvalueの位置を割合で返す

THREE.MathUtils.inverseLerp(0, 100, 50); //=> 0.5

lerp

開始値x, 終了値y, 割合tを渡す
tは0から1までの値で、返り値はxからyでtの割合に位置する数値となる。
例えばxが5, yが10でtが0.5の場合、5と10の中間の7.5が返る。
※上述のinverseLerpの返り値がtであるという関係性。

THREE.MathUtils.lerp(2, 4, 0.5); //=> 3

damp

lerp関数の拡張版みたいなもので、値の推移をよりなめらかにする関数。

現在値x, 目標値y, 係数lambda, デルタタイムdt*を渡す。
返り値は、次に現在値になるべき数値。

係数lambdaが大きいほど、値の変化がより急激になる（前半で一気に目標値に近づく）

let currentVal = 0;
setInterval(() => {
  currentVal = THREE.MathUtils.damp(currentVal, 100, 1, 0.1);
  console.log(currentVal);
}, 100);

*デルタタイム＝現在のフレームと前のフレームとの時間差

mapLinear

値input, 範囲1の開始値a1, 範囲1の終了値a2, 範囲2の開始値b1, 範囲2の終了値b2を渡す。
範囲1におけるinputの位置を出し、範囲2におけるその位置の値を返す。
言い換えれば、範囲1でinverseLerpを使いtを求め、tを用いて範囲2でlerpをしている。

THREE.MathUtils.mapLinear(50, 0, 100, 0, 1); //=> 0.5

pingpong

値xと、長さlengthを渡す。
0とlengthを壁と見立てて、
ピンポン玉が0とlengthの間を往復しながらxだけ進んだあとの、ピンポン玉の位置を返す。

THREE.MathUtils.pingpong(5, 3); //=> 1

ceilPowerOfTwo

引数nより大きな、または等しい2の累乗の数値を返す。

THREE.MathUtils.ceilPowerOfTwo(62); //=> 64

floorPowerOfTwo

引数nより小さな、または等しい2の累乗の数値を返す。

THREE.MathUtils.ceilPowerOfTwo(62); //=> 32

radToDeg

弧度法の角度（ラジアン）を度数法の角度に変換。
例は略

randFloat

2つの数値x, yを引数に取り、x以上y未満のランダムな小数を返す。
例は略

randFloatToSpread

引数range渡し、0を中心にrangeを範囲としてランダムな小数を返す。
たとえば20を渡した場合、-10以上10未満の値が返る。
計算としては　-range/2 以上 range/2 未満となる。

THREE.MathUtils.randFloatToSpread(100); //=> -50以上50未満の小数

randInt

randFloatの整数版

seededRandom

0以上1未満の疑似乱数を生成する。
引数sはシード値で、このシード値が同じの場合は何度試行しても必ず同じ数値が返ってくる。

//一回目
THREE.MathUtils.seededRandom(2); //=> 0.7342509443406016
//二回目
THREE.MathUtils.seededRandom(2); //=> 0.7342509443406016

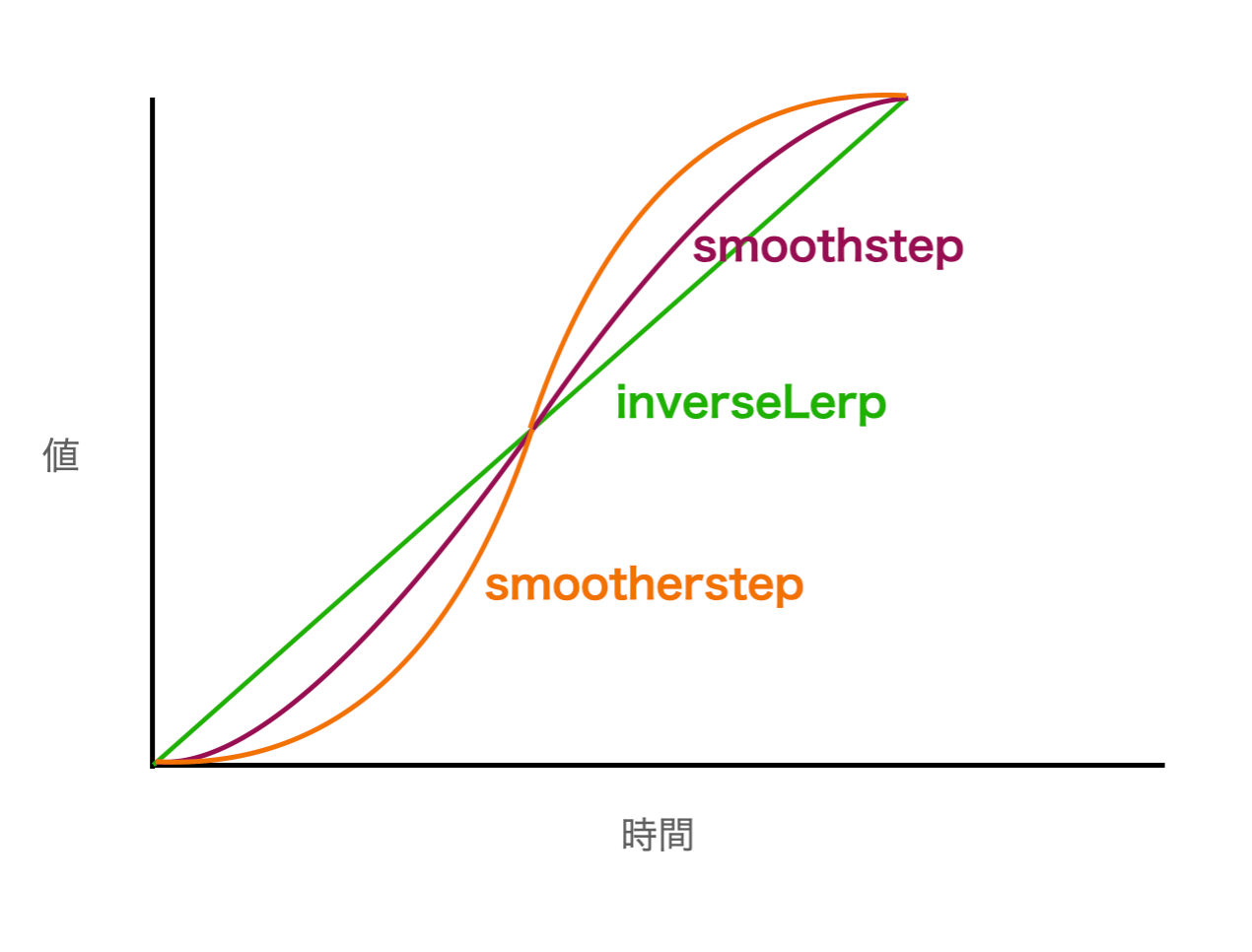
smoothstep

値x、最小値min, 最大値maxを渡す。
inverseLerpに近いが、inverseLerpが線形なのに対して、smoothstepはease-in-outのような滑らかな補正をかけて、位置を返してくれる。

smootherStep

smoothstepのより滑らか版。イメージ画像を参照(正確な曲線ではないです)

setQuaternionFromProperEuler

クオータニオンq、角度a, 角度b, 角度c、順番orderを渡す。
orderは'XYZ'や'YXZ'で、'XYZの場合は'aがx軸、bがy軸、cがz軸の角度となる。
角度はラジアンで表す。
これらのオイラー角情報をもとにクォータニオンを計算し、qに適用する。

const q = new THREE.Quaternion();
const x = THREE.MathUtils.degToRad(45);
const y = THREE.MathUtils.degToRad(15);
const z = THREE.MathUtils.degToRad(90);
THREE.MathUtils.setQuaternionFromProperEuler(q, x, z, y, 'XZY');

最後に

疲れました...
間違いがありましたら、優しく教えていただけると嬉しいです。