基本的な量子ゲートを理解して加算器・ドイチュのアルゴリズムをIBM Qで動かそう

はじめに

本記事では、量子ビットの数式的な表現、代表的な量子ゲートの役割を説明します。
その後、量子ゲートを用いて加算器（半加算器）とドイチュのアルゴリズムを IBM Q (IBM Quantum) で動かしてみた結果を報告します。

• 対象読者: 量子コンピュータの基本を学んでみたいIT系エンジニア・社会人や、情報系のバックグラウンドが多少ある高校生・大学生を想定しています。すでに物理学や量子力学を専門に学んでいる方には物足りない内容かと思います。
• 数学的な前提知識: 高校数学で勉強するような行列計算を知っていれば大丈夫です。本記事ではなるべく難しい数式を避けた表現を心がけています。そのため、あえて文字で一般化するような計算を避けたり、省略した記法を避けたりしています。

本記事の著者は寺田晃太朗です。情報工学系出身でIT系のエンジニア・研究者をしています。
これまで、アプリケーションレイヤーのツールとして量子アニーリングマシンを使った経験があります。最近、AIREV株式会社さんと一緒に量子コンピュータ・量子ゲートの勉強を始めているので、現時点のアウトプットとして本記事をまとめています。一緒に勉強中の他の方も執筆している量子コンピュータの活用についての調査・検証の記事一覧もぜひご覧ください。

量子ビットと古典ビットの違い

私たちの身近である古典ビット（古典回路）^[1] に馴染みがある方がほとんどだと思いますので、古典ビット（古典回路）と比較をしながら量子ビット（量子回路）の特徴を説明していきます。

まず形式的な違いを次の表にまとめます。

項目	量子ビット	古典ビット
状態	0, 1に確定した状態を持たないことがある。これを0と1を重ね合わせた状態といい、1量子ビットで無数の状態（アナログ値）を持つことができる。ただし、その量子ビットが測定される（またはその量子ビットとエンタングルメント状態にある別量子ビットの0, 1が確定される）と、状態は0または1に確定する。これを数式的にどのように表現できるかは後述する。	常に0, 1に確定したどちらかの状態（デジタル値）を持つ。
ノイズ	量子ビットが無数の状態（アナログ値）を持てることからノイズの影響をダイレクトに受けやすい。例えば、理論上では100%の確率で出力結果1が測定されるような量子回路でも、現在の実量子回路を動かすと出力結果0が測定されることがある。	古典ビットも物理的な電圧変動やノイズにより影響を受けるが、0または1のどちらかの状態（デジタル値）に常に収束されたり、誤り訂正回路が組み込まれていたりするので、論理的には問題ないことがほとんど。
実行回数	量子ビットを用いた量子回路では、以下の理由によりショットと呼ばれる回数分だけ複数回繰り返し回路を動かし、出力の確率を観測する。 ・量子ビットの状態は確率的に測定されるので、量子ビットの状態を推定するためのサンプリングによる統計的な誤差を小さくするため ・上の項目に記述したようにノイズの影響をダイレクトに受けるので測定回数を複数回重ねることでその影響を小さくさせたいため	古典ビットを用いた古典回路では、通常は1回だけ実行すれば結果が確定する。
回路	量子回路の例: 特徴: ・各量子ビットを表すワイヤは交わったり分岐したり入力側に戻ったりしない ・各量子ゲートの入出力数は同じ	古典回路（論理回路）の例: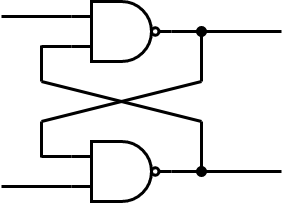 特徴: ・各ビットを表すワイヤが交わったり分岐したり入力側に戻ったりできる ・各ゲートの入力数と出力数が異なることもある

量子ビットの数式的表現

本章では、なるべく難しい数式を避けて量子ビット (qubit) の数式的な表現方法を説明します。

1量子ビット

「量子ビットと古典ビットの違い」の章で、1量子ビットは0と1の重ね合わた状態と表現しました。これを数式的には2つの複素数^[2] のペア（2次元の列ベクトル）で表します。結構、直感的です。

次のベクトルは1量子ビットを表しています。

$$\begin{align*} \begin{pmatrix} \alpha \\ \beta \\ \end{pmatrix} \end{align*}$$

$\alpha$, $\beta$ は複素数です。それぞれの複素数は0, 1の重なり度合いの重み係数のようなもの表しています（正確には確率振幅と呼ばれます）。
ただし、この表現において、後々の計算を便利にするために、$\left| \alpha \right|^2 + \left| \beta \right|^2 = 1$ という制約条件を設けます。複素数の絶対値の取り方は復習しておいてください。

このベクトルは次のようにも表現できます。

$$\begin{align*} \alpha \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix} + \beta \begin{pmatrix} 0 \\ 1 \\ \end{pmatrix} \end{align*}$$

ここで、$\begin{pmatrix}1 \\ 0 \\ \end{pmatrix}$ と $\begin{pmatrix}0 \\ 1 \\ \end{pmatrix}$ は一般的に採用される計算基底ベクトルで、ディラックのブラケット記法（というベクトルの便利な書き方）を用いてそれぞれ $| 0 \rangle$, $| 1 \rangle$ とも書けます。

そこで、ブラケット記法を用いると、先ほどのベクトルは、

$$\begin{align*} \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle \end{align*}$$

とも書け、0と1の重なりの重み係数がそれぞれ $\alpha$, $\beta$ であることを再確認できます。
なお、ディラックのブラケット記法は便利な表記ですが、慣れないと難しい（私もまだ慣れてない）ので本記事ではベクトルに書き下す表記を基本的に併記しています。

重ね合わせ状態であるこの量子ビットを「測定」すると、次のような挙動になります。

• $\left| \alpha \right|^2$ の確率で 0 が測定され、その後このビットは 0 の状態すなわち $\begin{pmatrix}1 \\ 0 \\ \end{pmatrix}$ に変化する。
• $\left| \beta \right|^2$ の確率で 1 が測定され、その後このビットは 1 の状態すなわち $\begin{pmatrix}0 \\ 1 \\ \end{pmatrix}$ に変化する。

なぜこのようになるかの理論的な背景は、量子力学をぜひ教科書で勉強してください。本記事では、このようになるという現象を認めてしまって、量子回路や量子コンピュータへどう利用していくかを説明していきます。

1量子ビットの具体例

以上の数式的表現をふまえ、1量子ビットの具体例をいくつか挙げます。

量子ビット	$\alpha$, $\beta$ の値	0が測定される確率	1が測定される確率
$\begin{pmatrix}1 \\ 0 \\ \end{pmatrix}$	$\alpha=1$, $\beta=0$	1 (= 100%)	0 (= 0%)
$\begin{pmatrix}0 \\ 1 \\ \end{pmatrix}$	$\alpha=0$, $\beta=1$	0 (= 0%)	1 (= 100%)
$\dfrac{5}{13} \begin{pmatrix}1 \\ 0 \\ \end{pmatrix} + \dfrac{12}{13} \begin{pmatrix}0 \\ 1 \\ \end{pmatrix}$	$\alpha=\dfrac{5}{13}$, $\beta=\dfrac{12}{13}$	$\left\lvert \dfrac{5}{13} \right\rvert^2 = \dfrac{25}{169}$ (= 15%)	$\left\lvert \dfrac{12}{13} \right\rvert^2 = \dfrac{144}{169}$ (= 85%)
$\dfrac{5}{13} i \begin{pmatrix}1 \\ 0 \\ \end{pmatrix} - \dfrac{12}{13} \begin{pmatrix}0 \\ 1 \\ \end{pmatrix}$	$\alpha=\dfrac{5}{13} i$, $\beta=-\dfrac{12}{13}$	$\left\lvert \dfrac{5}{13} i \right\rvert^2 = \dfrac{25}{169}$ (= 15%)	$\left\lvert -\dfrac{12}{13} \right\rvert^2 = \dfrac{144}{169}$ (= 85%)

4番目の具体例も正当な量子ビットです。3番目の例と測定される出力の確率は同じですが、$\alpha$, $\beta$ の符号が異なっていたり $i$ が掛けられていたりします。これは量子ビットの位相が異なっていることを表しています^[3]。位相だけが異なっているときは測定される確率は同じですが、他の量子計算と組み合わせたときの計算結果が位相によって異なることがあるため、位相の違いは量子回路や量子アルゴリズム全体を計算するときに重要な役割を担います。

複数量子ビット

複数量子ビットは、1量子ビットをそのまま拡張させた考え方で表現可能です。

例えば、1量子ビットは 0 と 1 の重ね合わせ^[4] だったのに対して、2量子ビットは 00, 01, 10, 11 の4状態の重ね合わせなので、次のような4次元の列ベクトルで表現できます。

$$\begin{align*} \begin{pmatrix} \alpha \\ \beta \\ \gamma \\ \delta \\ \end{pmatrix} = \alpha \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \\ \end{pmatrix} + \beta \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \\ \end{pmatrix} + \gamma \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \\ \end{pmatrix} + \delta \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \\ \end{pmatrix} \end{align*}$$

ディラックのブラケット記法を用いると次のようにも書けます。

$$\begin{align*} \alpha \left| 00 \right\rangle + \beta \left| 01 \right\rangle + \gamma \left| 10 \right\rangle + \delta \left| 11 \right\rangle \end{align*}$$

1量子ビットのときと同様に、$\left| \alpha \right|^2 + \left| \beta \right|^2 + \left| \gamma \right|^2 + \left| \delta \right|^2 = 1$ という制約を満たすようにします。

この2量子ビットを測定したとき、各状態が測定される確率は次の通りです。

• 00 が測定される確率: $\left| \alpha \right|^2$
• 01 が測定される確率: $\left| \beta \right|^2$
• 10 が測定される確率: $\left| \gamma \right|^2$
• 11 が測定される確率: $\left| \delta \right|^2$

具体的な2量子ビットの数式的な表現を次に例示します。

$$\begin{align*} \begin{pmatrix} 2 / 15 \\ - 4 / 15 \\ 6 i / 15 \\ - 13 i / 15 \\ \end{pmatrix} = \dfrac{2}{15} \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \\ \end{pmatrix} - \dfrac{4}{15} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \\ \end{pmatrix} + \dfrac{6}{15} i \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \\ \end{pmatrix} - \dfrac{13}{15} i \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \\ \end{pmatrix} \end{align*}$$

各状態が測定される確率は次の通りです。

• 00 が測定される確率: $\left| \dfrac{2}{15} \right|^2 = \dfrac{4}{225}$ (= 2 %)
• 01 が測定される確率: $\left| - \dfrac{4}{15} \right|^2 = \dfrac{16}{225}$ (= 7 %)
• 10 が測定される確率: $\left| \dfrac{6}{15} i \right|^2 = \dfrac{36}{225}$ (= 16 %)
• 11 が測定される確率: $\left| - \dfrac{13}{15} i \right|^2 = \dfrac{169}{225}$ (= 75 %)

以上は2量子ビットの例でしたが、3量子ビット以上も同様に考えることができます。

基本的な量子ゲート

本章では、いよいよ量子ビットを操作させる作用を持つ「量子ゲート」を説明していきます。

代表的な量子ゲートとして、H, X, Y, Z, CNOT, トフォリゲートを本記事では説明します。他にもS, Tゲート, SWAP, CZゲートなど有名なゲートがあるので、興味がある方はウェブ検索するか関連書籍を調べてみてください。

量子ゲートの操作は行列

前章では、量子ビットはベクトルで表現できることを説明しました。量子ゲートは量子ビットを操作する役割を持ちます。

列ベクトルを別の列ベクトルに変化させるには、行列を列ベクトルに対して左から掛けることで数式的に表現できます。
例えば、1量子ビットは2次元列ベクトルで表現されますが、$2 \times 2$ の行列をこのベクトルに左から掛けることで、別の2次元列ベクトルが計算結果として出てきます。つまり、それぞれの量子ゲートには対応する行列^[5] が存在します。

1入力・1出力の量子ゲート

Hゲート (Hadamardゲート)

Hadamardはアダマールと読みます。
アダマールゲートは 0 と 1 の重ね合わせ状態を生成するような操作をするゲートです。一番簡単に「量子っぽい」動きを確認できるので最初に説明します。

IBM Q では次のような記号で表されます。

Hゲートの行列表現は次のとおりです。

$$\begin{align*} H = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \\ \end{pmatrix} \end{align*}$$

Hゲートを 0 に対して作用させてみます。

$$\begin{align*} H \left| 0 \right\rangle = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \\ \end{pmatrix} \end{align*}$$

この状態はブラケット記法を用いると次のように表現できます。

$$\begin{align*} \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix} + \dfrac{1}{\sqrt{2}} \begin{pmatrix} 0 \\ 1 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \left| 0 \right\rangle + \dfrac{1}{\sqrt{2}} \left| 1 \right\rangle \end{align*}$$

つまり、Hゲートを用いることで、0 から「0と1が等しく重なり合った状態」を生成できました。
0が測定される確率は $\left| \dfrac{1}{\sqrt{2}} \right|^2 = 0.5$ で、1が測定される確率も同じく $0.5$ です。

Hゲートを 1 に対して作用させると、同じように「0と1が等しく重なり合った状態」を生成できます。ただし、位相が先ほどと異なります。

$$\begin{align*} H \left| 1 \right\rangle = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 1 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ -1 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \left| 0 \right\rangle - \dfrac{1}{\sqrt{2}} \left| 1 \right\rangle \end{align*}$$

HゲートをIBM Qで動かす

実際に、実機の量子コンピュータ IBM Q (IBM Quantum) でアダマールゲートを動かしてみましょう。

次の図のような量子回路を組んでみます。
左端が入力の 0 の状態で^[6]、アダマールゲートを作用させた後、一番右で量子ビットを測定しています。

上で計算した理論によれば、0と1が等しい確率で測定されるはずです。

1024ショット実行した結果は次のようになりました。

ほぼ等確率でどちらの状態も測定されることが確認できました。微妙に異なっている理由は、これはサンプリングなので、1024回の試行でも必ずしも同じ回数に割れるわけではないのと、前述の物理的なノイズの影響のためです。

Xゲート (NOTゲート)

Xゲートはビット反転をするゲートです。その役割からNOTゲートとも呼ばれます。

IBM Q では次のような記号で表されます。「X」と書かれていないので注意してください。

Xゲートの行列表現は次のとおりです。

$$\begin{align*} X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \end{align*}$$

なぜビット反転なのかは実際に計算してみるとわかります。

$$\begin{align*} X \left| 0 \right\rangle = \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ \end{pmatrix} = \left| 1 \right\rangle \end{align*}$$

$$\begin{align*} X \left| 1 \right\rangle = \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix} = \left| 0 \right\rangle \end{align*}$$

0が1、1が0に、それぞれ変化します。

Yゲート

Yゲートもビット反転をするゲートです。Xゲートとの違いはビット反転に加えて位相も反転します。

IBM Q では次のような記号で表されます。

Yゲートの行列表現は次のとおりです。

$$\begin{align*} Y = \begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix} \end{align*}$$

Yゲートを 0 に対して作用させてみます。

$$\begin{align*} Y \left| 0 \right\rangle = \begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix} = \begin{pmatrix} 0 \\ i \\ \end{pmatrix} = i \left| 1 \right\rangle \end{align*}$$

これを測定すると $\left| i \right|^2 = 1$ の確率で 1 が測定されるため、ビット反転の役割を確認できますが、同時に位相が変化していることがわかります。この例では位相の変化は測定に反映されませんが、今後量子ゲートを組み合わせた量子回路で計算する際に、位相の違いが重要な役割を担うことがあります。

同じように、Yゲートを 1 に対して作用させてみます。

$$\begin{align*} Y \left| 1 \right\rangle = \begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} -i \\ 0 \\ \end{pmatrix} = -i \left| 0 \right\rangle \end{align*}$$

同様にこれを測定すると $\left| -i \right|^2 = 1$ の確率で 0 が測定されるため、ビット反転の役割を確認できます。

Zゲート

Zゲートは位相反転させるゲートです。0, 1に作用させても位相は反転しますが、ビットは反転しません。

IBM Q では次のような記号で表されます。

Zゲートの行列表現は次のとおりです。

$$\begin{align*} Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} \end{align*}$$

Zゲートを 0 に対して作用させてみます。

$$\begin{align*} Z \left| 0 \right\rangle = \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix} = \left| 0 \right\rangle \end{align*}$$

何も変わりません。

Zゲートを 1 に対して作用させてみます。

$$\begin{align*} Z \left| 1 \right\rangle = \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} 0 \\ -1 \\ \end{pmatrix} = - \left| 1 \right\rangle \end{align*}$$

測定したときに 1 が100%の確率であることは変わりませんが、位相が変化しています。

測定

測定 (measurement) は、ゲートとは違うかもしれませんが、量子ビットを測定する部品です。

IBM Q では次のような記号で表されます。
ここで上半分で横に貫いている実線は量子ビットのワイヤで、下半分で横に貫いている二重線は古典ビットのワイヤです。

量子ビットを測定すると、測定された状態 (0 または 1) を人間などが認識できるようになるとともに、その量子ビットは測定された状態へと変化します。

2入力・2出力の量子ゲート

1入力・1出力の量子ゲートは $2 \times 2$ の行列で表現されたように、2入力・2出力の量子ゲートは $4 \times 4$ の行列で表現されます。

CNOTゲート

CNOTゲートは2入力・2出力の量子ゲートの1つです。
入力の一方を「コントロールビット」、他方を「ターゲットビット」と呼びます。
CNOTゲートの操作を言葉で表すと「コントロールビットが1のときのみターゲットビットを反転する（Xゲートの操作をする）」です。

具体的な動作は次のとおりです。ここで1番目のビットをコントロールビット、2番目のビットをターゲットビットとします。入力が重ね合わせの場合にどうなるかは後で説明します。

• 「00」を入力 → 出力は「00」
• 「01」を入力 → 出力は「01」
• 「10」を入力 → 出力は「11」 (このときターゲットビットが反転)
• 「11」を入力 → 出力は「10」 (このときターゲットビットが反転)

IBM Q では次のような記号で表されます。
上のビットがコントロールビットで、下のビットがターゲットビットです。

CNOTゲートの行列表現は次のとおりです。

$$\begin{align*} {\it CNOT} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \end{align*}$$

CNOTゲートに 10 を入力した結果を計算してみます。上で説明したように、結果は「11」になるはずです。

$$\begin{align*} {\it CNOT} \left| 10 \right\rangle = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \\ \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \\ \end{pmatrix} = \left| 11 \right\rangle \end{align*}$$

計算でも確認できました。

3入力・3出力の量子ゲート

3入力・3出力の量子ゲートは $8 \times 8$ の行列で表現されます。

トフォリゲート

トフォリ (Toffoli) ゲートは3入力・3出力の量子ゲートの1つです。
入力のうち2個を「コントロールビット」、他方を「ターゲットビット」と呼びます。
トフォリゲートの操作を言葉で表すと「コントロールビットがどちらも1のときのみターゲットビットを反転する（Xゲートの操作をする）」です。

具体的な動作は次のとおりです。ここで1番目と2番目のビットをコントロールビット、3番目のビットをターゲットビットとします。

• 「000」を入力 → 出力は「000」
• 「001」を入力 → 出力は「001」
• 「010」を入力 → 出力は「010」
• 「011」を入力 → 出力は「011」
• 「100」を入力 → 出力は「100」
• 「101」を入力 → 出力は「101」
• 「110」を入力 → 出力は「111」 (このときターゲットビットが反転)
• 「111」を入力 → 出力は「110」 (このときターゲットビットが反転)

IBM Q では次のような記号で表されます。
上の2個のビットがコントロールビットで、下のビットがターゲットビットです。

Toffoliゲートの行列表現は次のとおりです。

$$\begin{align*} {\it Toffoli} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ \end{pmatrix} \end{align*}$$

複数量子ビットの一部に対して量子ゲートを作用させるときの計算方法

これまでゲート単体の計算方法は説明しましたが、複数量子ビットの一部に対してゲートを作用させたときはどのように計算すればいいでしょうか。
例えば、次の例のように、2量子ビットの1番目のビットにはHゲート、2番目のビットにはXゲートを掛け、その後1番目をコントロールビット・2番目をターゲットビットとしたCNOTゲートを作用させるとどのような結果になるか、計算したいと思います。

複数ビットに対する操作を行列で表現するには「テンソル積 $\otimes$」を用いることができます。

具体的に上の例のように、1番目のビットにはHゲート、2番目のビットにはXゲートを同時に作用させる操作を $H \otimes X$ で表します。

ここでテンソル積の計算ルールとして以下を用います。

$$\begin{align*} \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} \otimes \begin{pmatrix} w & x \\ y & z \\ \end{pmatrix} = \begin{pmatrix} aw & ax & bw & bx \\ ay & az & by & bz \\ cw & cx & dw & dx \\ cy & cz & dy & dz \\ \end{pmatrix} \end{align*}$$

計算ルールにしたがって、$H \otimes X$ を計算すると、

$$\begin{align*} H \otimes X = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \\ \end{pmatrix} \otimes \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 \\ \end{pmatrix} \end{align*}$$

になります。初期状態「00」にこれを作用させると、

$$\begin{align*} (H \otimes X) \left| 00 \right\rangle = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 1 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \left| 01 \right\rangle + \dfrac{1}{\sqrt{2}} \left| 11 \right\rangle \end{align*}$$

のように、01 と 11 の重ね合わせ状態になることが計算されます。
まあ、直感的にも1ビット目にアダマールゲートを掛け、2ビット目にNOTゲートを掛けているので、01 と 11 になることは想像できますが、計算でも確かめられます。

続いて、この2量子ビットの重ね合わせ状態に対して、CNOTゲートを作用させます。

$$\begin{align*} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \dfrac{1}{\sqrt{2}} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 1 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 0 \\ 1 \\ 1 \\ 0 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \left| 01 \right\rangle + \dfrac{1}{\sqrt{2}} \left| 10 \right\rangle \end{align*}$$

最終的な出力結果は 01 と 10 の等確率での重ね合わせだとわかりました。
なお、これが、上で書いたCNOTゲートのコントロールビットの「入力が重ね合わせの場合」の答えです。答えは、ターゲットビットに対するXゲートの計算が同時に実行されます。

実際にこの回路を IBM Q の実機で動かすと、次のような結果が得られました。

1024ショットのうち、多くのケースで 01 または 10 が等確率で得られるサンプリング結果が得られました。計算通りです。

IBM Qを用いて実際に少し意味のある量子回路を動かしてみる

以上で、すべてではありませんが代表的な量子ゲートを説明しました。
これらのゲートを用いて、（先ほどの動作確認程度よりも）少し意味のある計算を、量子ゲート回路を組んで計算してみようと思います。

加算器（半加算器）

まず、古典回路（論理回路）で入門的な回路として取り上げられる半加算器を、量子ゲートを用いた量子回路として作成してみます。
半加算器は、2ビットを入力として、1ビット範囲での加算結果（和）と桁上がりビットの合計2ビットを出力する回路です。

これを量子回路で表現すると次の図のようになります。

半加算器の量子回路

※回路図中の縦に入っている破線は「バリア」であり、ゲートの位置を揃えるために挿入しています。バリアは動作に対しては特に影響を与えません。

量子回路の特徴として途中でビットを増やすことができないため、最初から出力ビットの分も含めて3量子ビット分のワイヤを用意しておきます。

まず、1ビット範囲での加算結果は入力の2ビットのXORを取ることで計算できます。これにはCNOTゲートをそのまま利用することで実現できます。次の表を見ると動作に問題がないことを確認できます。

入力A	入力B	CNOTの結果 (= 入力Aが1のときのみ入力Bを反転)
0	0	0
0	1	1
1	0	1
1	1	0

続いて、桁上がりビットは、2つの入力がともに1のときに限り、1となるため、2つの入力をコントロールビットとするトフォリゲートを用いれば問題ないです。

最後に、必要な量子ビットのみ（つまり加算結果と桁上がりのビットのみ）を測定します。

上で図示した回路では、動作を確認するために入力データとして 11 をXゲートを用いて生成しています。$1 + 1 = 2_{(10)} = 10_{(2)}$^[7] なので、結果は「10」になることが期待されます。

回路をIBM Qで実装し^[8]、実機で動かすと、次の結果が得られました。

期待どおり「10」の結果が得られました。

これだけだと、単に古典の論理回路を量子回路として実装し直しただけに過ぎません。
次に、量子計算っぽい挙動を確認するために、半加算器の演算部分は同じにしたまま、入力データを次のように変更してみます。

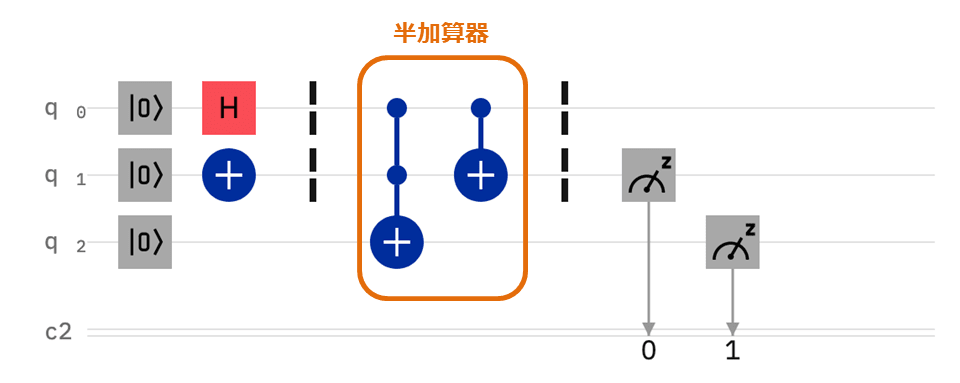
一方のビットは1で固定なのに対し、他方のビットはアダマールゲートを用いることで0と1の重ね合わせ状態を生成しています。
よって、計算結果として、

• $1 + 1 = 2_{(10)} = 10_{(2)}$
• $0 + 1 = 1_{(10)} = 01_{(2)}$

の重ね合わせ状態が出力されることが期待されます。

回路をIBM Qで実装し、実機で動かしてみましょう。次の結果が得られました。

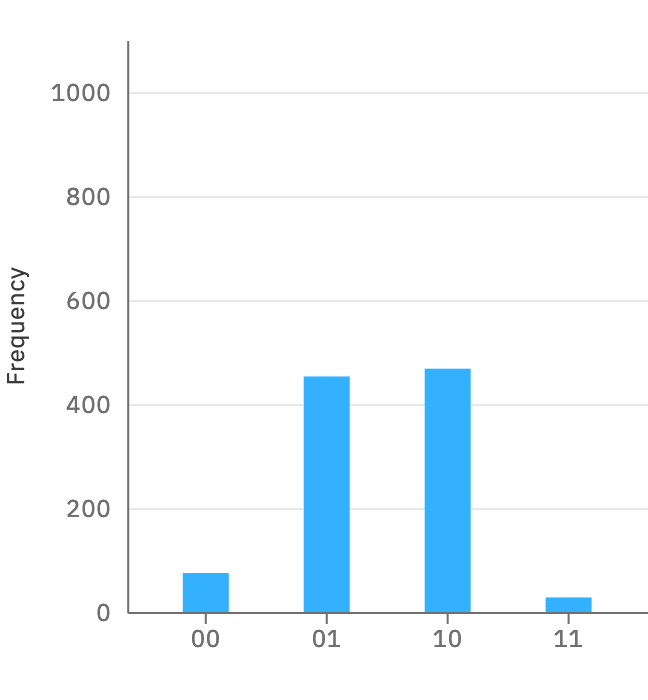
期待どおり「10」と「01」が等確率で重ね合わせられた状態の結果が得られました。

可逆性のある量子加算器

量子回路が持つ古典回路にない特徴として、ゲートが可逆性を持っていることが知られています。
これを確かめるために、具体的に量子回路を動かしてみましょう。

上で実装した量子加算器を「左右対称」に組み替えてみて^[9]、先ほどの出力側からデータを入れてみましょう。
つまり、次のような量子回路を考えます。これを「逆加算器」と呼ぶことにします。

「逆加算器」の量子回路

右側が元の加算器の入力側（この逆加算回路では出力）で、左側が元の加算器の出力側（この逆加算回路では入力）です。

逆加算器に入力として「01」を入れることで、加算の答えが「$01_{(2)} = 1_{(10)}$」になるような入力を逆加算器が見つけてくれることを期待します。つまり、答えが「01」となるような加算の元データである「01」または「10」が、逆加算器の出力として出てきて欲しいです。なお、入力1ビット目にはアダマールゲートを意図的に入れています。

この回路をIBM Qで実装し、実機で動かすと、次の結果が得られました。

期待どおり「01」と「10」が等確率で重ね合わせられた状態が測定される結果が得られました。
この結果から可逆性の性質を持つ量子回路を利用して、通常方向の演算回路を逆に実装することで、欲しい答えを入力すると演算結果としてその答えを出力するような入力を量子コンピュータが計算してくれることがわかりました。

で、何が嬉しいのか？

半加算器を量子回路で実装して動作を確認したところで、「で？」という感想を持ってもしかたないと思います。実際、すでに古典回路（論理回路）で実現されている回路を量子回路で再実装したところでの実用上のメリットは現在のところ特にありません。なんなら逆に確率的に答えを間違えてしまうので劣化では？と感じたとしてもおかしくはありません。でも、より複雑な量子アルゴリズムの中の一部として加算を実現したいときには利用できるかもしれません。上の具体例では実際に量子ゲートの動作を確認するために、理解しやすい加算器を取り上げて説明したという意図でした。

ところが、一部問題に対しては、量子アルゴリズムを量子回路で実装すると、古典的なアルゴリズムと比較して効率的な実行時間で計算できることがわかっています。そのような問題の中でも単純な部類の問題である「ドイチュの問題」を解く量子アルゴリズムとその量子回路での実装を次に紹介します。

ドイチュのアルゴリズム

ようやく量子アルゴリズムが本領発揮する場面を紹介していきます。

ドイチュの問題（Deutschの問題・ドイチェの問題・ドイチの問題・ドイッチュの問題）とは次のような問題です:

---

あるブラックボックス関数（オラクル）が与えられます。私たちはこのブラックボックス関数の中身（実装）を知ることはできません。このブラックボックス関数は 0 または 1 の整数を入力として受け取ると、0 または 1 の整数を出力します。このブラックボックス関数が、Constantな関数かBalancedな関数のどちらかを判断してください。

• Constantな関数とは: 0と1のどちらを入力しても、必ず0または1のどちらか一方が出力される関数。
• Balancedな関数とは: 0を入力すると0が出力され1を入力すると1が出力される、もしくは0を入力すると1が出力され1を入力すると0が出力されるような関数。

---

古典アルゴリズムでのこの問題の解法を考えると、必ず2回ブラックボックスを動かしてみる（＝オラクルに問い合わせる）必要があります。
なぜなら、まずブラックボックス関数に0を入力したときの出力を調べたとしても、それが0であろうと1であろうとまだ関数のタイプがどちらかを判断できずに、1を入力したときの出力を知って初めてそれを判断できるためです。最初から1を入力して調べても同じことです。

これに対し、ドイチュのアルゴリズム（量子アルゴリズム）を用いることで、1回だけブラックボックスを動かす（＝オラクルに問い合わせる）ことで関数のタイプがどちらかを判断できます。

ドイチュのアルゴリズム（量子回路）を次の図に示します。

計算結果の1ビット目を測定して、

• 結果が 0 なら「Constantな関数」
• 結果が 1 なら「Balancedな関数」

と判断することができます。

なぜこの判断方法で問題がないのか、具体的に計算して確かめてみます。文字のまま計算することも可能ですが、実際のパターンごとに計算するほうがわかりやすいので具体的に場合分けして計算してみます。

この問題で考えられる関数のパターンとしてconstantで2通りとbalancedで2通りの合計4通り考えられます。

Constant: 関数 $f(0) = f(1) = 0$ の場合

オラクル

私たちはオラクルの中身を知ることはできませんが、入出力関係からオラクルの動作を再現することはできます。まず、このときのブラックボックス関数（量子オラクル）は、$I$ ゲートを用いて次のように実装できます。
※ $I$ ゲートは恒等ゲートです。何も操作しないゲートです。

なぜならこの回路で入力0と1に対して、次の動作になるからです。0と1のどちらの入力に対しても0を出力します。

入力	出力
00	00
10	10

※入力の1ビット目がオラクルへの入力で、出力の2ビット目がオラクルの出力

回路

このオラクル回路をドイチュのアルゴリズムに組み込むと次の図のようになります。

計算

実機で動かしてみる前に、計算して各ステップで量子ビットの状態がどのように変化するか、確かめてみます。

オラクルへの入力の直前の部分での2量子ビットの状態は、アダマールゲートを初期状態の2ビットに対して作用させることで生成されます。

$$\begin{align*} (H \otimes H) \left| 01 \right\rangle = \dfrac{1}{2} \begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \\ \end{pmatrix} = \dfrac{1}{2} \begin{pmatrix} 1 \\ -1 \\ 1 \\ -1 \\ \end{pmatrix} \end{align*}$$

次のステップで、この状態をオラクルに入力しますが、このケースではオラクルは何もしないので、オラクルから出力されたところでの状態は変わらないです。

オラクルの出力状態に対し、最後のステップで、1ビット目にアダマールゲートを掛けます。

$$\begin{align*} (H \otimes I) \cdot \dfrac{1}{2} \begin{pmatrix} 1 \\ -1 \\ 1 \\ -1 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 \\ \end{pmatrix} \dfrac{1}{2} \begin{pmatrix} 1 \\ -1 \\ 1 \\ -1 \\ \end{pmatrix} \\ = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ -1 \\ 0 \\ 0 \\ \end{pmatrix} = \dfrac{1}{\sqrt{2}} \left| 00 \right\rangle - \dfrac{1}{\sqrt{2}} \left| 01 \right\rangle \end{align*}$$

これでアルゴリズム終了時点での量子ビットの状態を計算できました。確かに、最後の状態の1ビット目を測定すると、必ず 0 になることが計算で確認できました。

実機

実際に、IBM Qの実機で動かしてみると、次の結果が得られました。

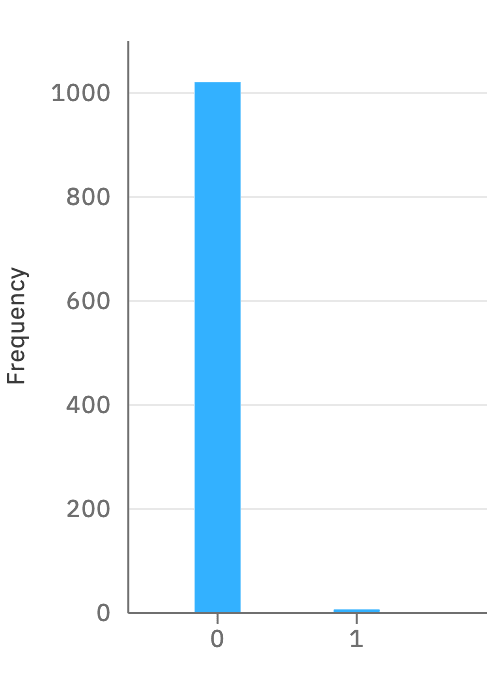
Constantな関数なので正しく 0 が得られていることを確認できます。

Constant: 関数 $f(0) = f(1) = 1$ の場合

オラクル

このときのブラックボックス関数（量子オラクル）は、Xゲートを用いて次のように実装できます。

なぜならこの回路で入力0と1に対して、次の動作になるからです。0と1のどちらの入力に対しても1を出力します。

入力	出力
00	01
10	11

※入力の1ビット目がオラクルへの入力で、出力の2ビット目がオラクルの出力

回路

このオラクル回路をドイチュのアルゴリズムに組み込むと次の図のようになります。

計算

計算はほぼ同様なので省略しますが、最後の状態の1ビット目を測定すると、必ず 0 になることが計算で確認できます。気になる方は計算して確かめてみてください。

実機

実際に、IBM Qの実機で動かしてみると、次の結果が得られました。

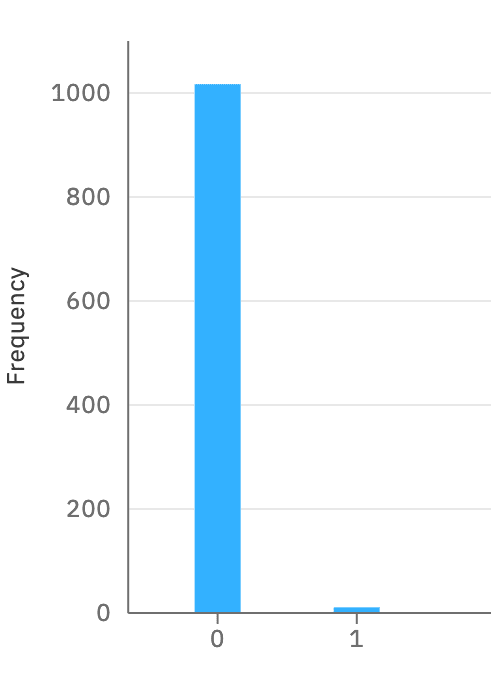
これもConstantな関数なので正しく 0 が得られていることを確認できます。

Balanced: 関数 $f(0) = 0, f(1) = 1$ の場合

オラクル

このときのブラックボックス関数（量子オラクル）は、CNOTゲートを用いて次のように実装できます。

なぜならこの回路で入力0と1に対して、次の動作になるからです。入力値と同じ値を出力します。

入力	出力
00	00
10	11

※入力の1ビット目がオラクルへの入力で、出力の2ビット目がオラクルの出力

回路

このオラクル回路をドイチュのアルゴリズムに組み込むと次の図のようになります。

計算

計算はほぼ同様なので省略しますが、最後の状態の1ビット目を測定すると、必ず 1 になることが計算で確認できます。気になる方は計算して確かめてみてください。

実機

実際に、IBM Qの実機で動かしてみると、次の結果が得られました。

Balancedな関数なので正しく 1 が得られていることを確認できます。

Balanced: 関数 $f(0) = 1, f(1) = 0$ の場合

オラクル

このときのブラックボックス関数（量子オラクル）は、CNOTゲートとXゲートを用いて次のように実装できます。

なぜならこの回路で入力0と1に対して、次の動作になるからです。入力値と異なる値を出力します。

入力	出力
00	01
10	10

※入力の1ビット目がオラクルへの入力で、出力の2ビット目がオラクルの出力

回路

このオラクル回路をドイチュのアルゴリズムに組み込むと次の図のようになります。

計算

計算はほぼ同様なので省略しますが、最後の状態の1ビット目を測定すると、必ず 1 になることが計算で確認できます。気になる方は計算して確かめてみてください。

実機

実際に、IBM Qの実機で動かしてみると、次の結果が得られました。

これもBalancedな関数なので正しく 1 が得られていることを確認できます。

この問題をより一般的にし、ブラックボックス関数の入力値として0または1だけでなく任意長のビット列を受け取れる関数を考える「ドイチュ・ジョザ (Deutsch-Jozsa) の問題」と「ドイチュ・ジョザのアルゴリズム」もあるので、興味がある方は調べてみてください。

で、何が嬉しいのか？（再）

ドイチュの問題に対しては、古典アルゴリズムではオラクルに対して少なくとも2回問い合わせないと問題が解けないのに対し、量子アルゴリズムではオラクルに対して1回問い合わせるだけで問題を解けることがわかりました。これは量子コンピュータのほうが問い合わせ回数の計算量で勝っていることを意味しています（上で紹介したドイチュ・ジョザのアルゴリズムでは入力ビット長 $n$ に対してこの差がさらに広がります）。でも、ドイチュの問題を速く解けるようになると、何が嬉しいのでしょうか？

ドイチュの問題は、量子コンピュータの歴史でも初期に考えられた問題であり（というかドイチュ先生が量子コンピュータの概念を提唱した先生なので）、量子アルゴリズムが古典アルゴリズムに計算量で勝てるようにある意味で恣意的に作られた問題と言ってもそんなに的外れな言い方ではないと思います。これがダイレクトに実用的な問題や実用的な問題解決法につながるかを考えるのは私の頭ではかなりハードだし、相当の想像力が必要だと思います。

しかし、この問題とアルゴリズムの提案によって、量子コンピュータ・量子アルゴリズムが古典コンピュータに対して有利な問題が存在することが示されたことは事実です。このようなアイデアが起点となり発展して、現在のより発展した量子アルゴリズムや実用化に向けた量子機械学習、量子化学計算へとつながり、研究が進められているようです（おおざっぱなまとめ方ですみません）。
より実用性が高まったアルゴリズムとして、グローバーの探索アルゴリズムやショアの素因数分解アルゴリズムが有名です。他にも多くの量子アルゴリズムは Quantum Algorithm Zoo というウェブサイトでまとめられています。ただし、これらの多くは現実規模の問題を考えると多数の量子ビットを必要とするlong-termアルゴリズムなので、直近で現実的に実現可能な量子ビット数で動作可能なNISQアルゴリズムも研究されています。

今後、より発展した量子アルゴリズムなどを、次回以降で報告をしたいと考えています。

参考文献

• 嶋田義皓: 「量子コンピューティング 基本アルゴリズムから量子機械学習まで」，オーム社，第1版，2020.

脚注

1. 古典ビット（古典回路）は「古典」と呼ばれますが現役バリバリ最先端で利用されている技術です。個人的に古典と呼ばれるのには違和感がありますが、量子力学の分野では量子ではないものを古典と呼ぶ文化があります。本記事では、それに沿った表記にしています。

2. 本記事（というか量子力学）では、虚数単位として $i$ を用います。

3. 位相についてより詳細については、量子ビットの一般型の表現やブロッホ球を理解すると把握できると思います。本記事では割愛します。

4. 本来「$\left| 0 \right\rangle$ と $\left| 1 \right\rangle$ の重ね合わせ」と書くのが正しいですが、ブラケット記法への抵抗感を無くすことでのわかりやすさ重視と、本文での表記の違いによって誤解が発生する可能性は少ないと考えてあえてシンプルに表記しています。本記事では以降もそのように表記します。

5. この行列はユニタリ行列である必要がありますが、その説明のためにより深い数学的な知識（線形代数）が必要になるため本記事では省略します。詳細は教科書や関連書籍を参照してください。

6. 「$\left| 0 \right\rangle$」を左端に挿入しなくても 0 で初期化されますが、見た目のわかりやすさのためにあえて「$\left| 0 \right\rangle$」を挿入しています。

7. 下付きの数字は進数を表しています。

8. QiskitなどのSDKを用いることで、回路をプログラミングで組み立てることができますが、今回はIBM QウェブサイトのGUI上で手作業で回路を組んでいます。

9. 図的には左右対称（前後逆転）すればいいですが、演算の行列としては元の行列の逆行列で表現できます。