決定性チューリング機械から量子チューリング機械へ

現在のコンピュータのモデルについて

現在のコンピュータ（ノイマン型コンピュータ）の数学的モデルは、1936年頃にイギリスの数学者であるアラン・チューリング（Alan Turing）により考案されました。このモデルがチューリング機械（Turing Machine）と呼ばれるものです。

チューリング機械は図1のように、記号が書き込まれる（無限に長い）テープとそのテープ上を左右に移動するヘッド、そして有限個の状態を持つ有限制御部を構造として持ちます^[1]。

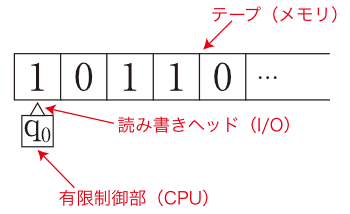
図1: チューリング機械

チューリング機械はノイマン型コンピュータの原型（論理的モデル）であり、それぞれ以下のように対応します。

チューリング機械	ノイマン型コンピュータ
テープ	記憶装置（メモリ）
有限制御部	制御装置（CPU）
ヘッド	入出力装置（I/O）

チューリング機械では、現在の制御部の状態 $Q = \lbrace q_{0}, \, q_1, \, \cdots \rbrace$（初期状態、および終了状態の集合を含みます）とヘッド位置のテープの記号 $\Sigma = \lbrace 0, \, 1, \, B \rbrace$（空白を表現する記号 $B$ を含みます）によって、次の制御部の状態と、ヘッド位置に書き込む記号、およびヘッドが動く方向 $\Delta = \lbrace L, \, R, \, N \rbrace$ （$L$は左、$R$は右、$N$は動かない）が決まります。
このようなチューリング機械の動作は、状態遷移関数 $\delta$ を用いて以下のように表現することができます。

$$\begin{align*} \delta(q_0, 0) &= (q_0, 0, R)\\ \underbrace{\textcolor{red}{Q \times \Sigma}}_{\text{定義域}} &\textcolor{red}{\rightarrow} \underbrace{\textcolor{red}{Q\times \Sigma \times \Delta}}_{\text{値域}} \end{align*}$$

例えば、以下の式(1)は、「チューリング機械の有限制御部の状態が $q_0$ で、ヘッドが $1$ を読んでいるならば、状態を $q_0$ に変え、ヘッド位置に $1$ を上書きした後に、ヘッドを右 $(R)$ へ $1$ マス移動させよ」と読むことができます。

$$\delta(q_0, 1) = (q_0, 1, R)\tag{1}$$

このように、有限制御部の状態およびヘッドが読んでいるテープ記号により出力が一意に定まるようなチューリング機械を、決定性チューリング機械（Deterministic Turing Machine: DTM）と呼びます。決定性チューリング機械では、入力を全て読み終え計算が終了した際に、その結果の状態が終了状態として定義されている集合に含まれる要素であれば「受理」、そうでなければ「拒否」となります。

非決定性チューリング機械と確率的チューリング機械

非決定性チューリング機械

決定性チューリング機械とは異なり、有限制御部の状態とヘッド位置の記号により状態遷移が一意に定まらないようなチューリング機械を、非決定性チューリング機械（Non-deterministic Turing Machine: NTM）と呼びます。図2に示すように、決定性チューリング機械は状態遷移が一本の道で定まるのに対し、非決定性チューリング機械は状態遷移が分岐している木構造として考えることができます^[2]。

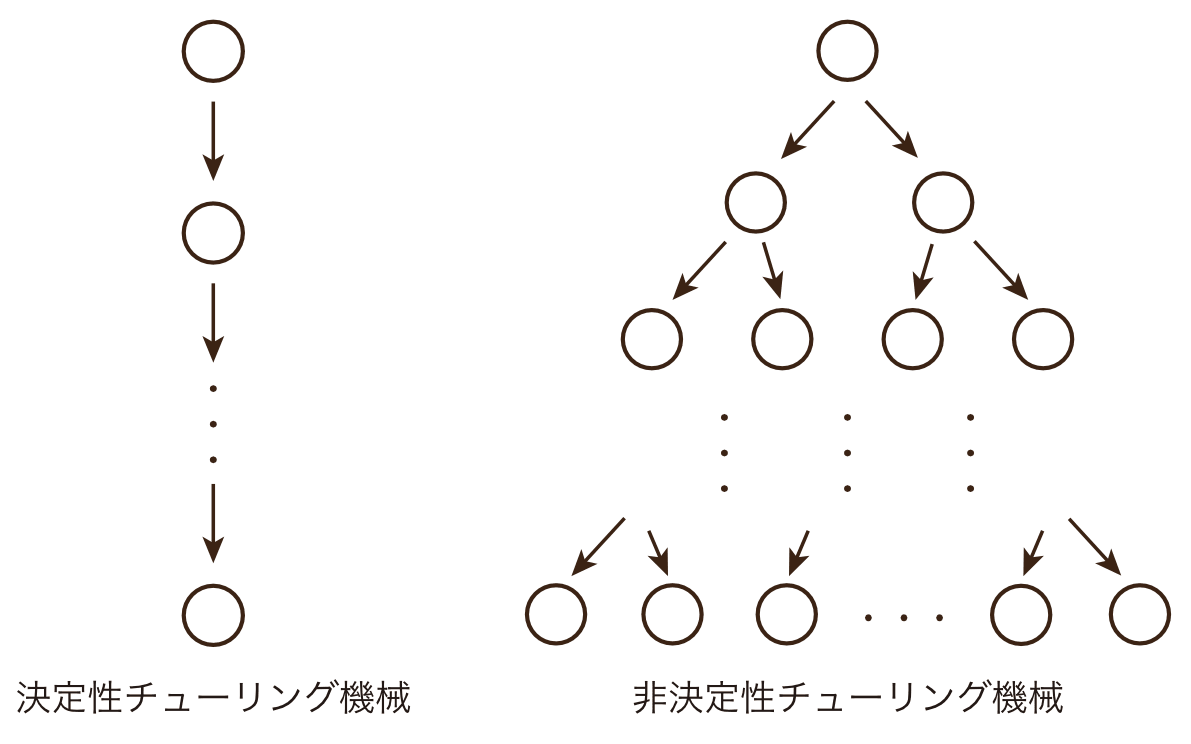
図2: 決定性チューリング機械と非決定性チューリング機械

非決定性チューリング機械は木構造の全ての経路をそれぞれ一つの決定性チューリング機械として表現することが可能なため、仮に全通りが $m$ 個の場合には $m$ 個の決定性チューリング機械を同時並列的に処理することと同値であると考えることができます。

図3: $m$個の決定性チューリング機械による表現

非決定性チューリング機械においては、受理の状態となる経路が１つでも存在する場合は「受理」となり、全ての経路において受理の状態で終わるパターンがない場合（全ての経路において拒否の状態となる場合）に「拒否」となります。

確率的チューリング機械

非決定性チューリング機械を、その遷移が確率的に選択されるよう乱数を用いてモデル化したものを確率的チューリング機械（Probabilistic Turing Machine: PTM）と呼びます。
この確率的チューリング機械の状態遷移関数 $\delta$ は以下のように表現することができます。

$$\begin{align*} \delta(q_0, 0, q_0, 0, R) &= \alpha\tag{2}\\ \textcolor{red}{Q \times \Sigma \times Q \times \Sigma \times \Delta} &\textcolor{red}{\rightarrow} \textcolor{red}{[0, 1]} \end{align*}$$

• $Q$: 状態の有限集合
• $\Sigma$: テープ記号の有限集合
• $\Delta$: ヘッドの移動方向

式(2)は、状態遷移関数 $\delta$ の第3〜第5引数までの $(q_0, 0, R)$ という決定性チューリング機械の状態遷移が起こる確率が $\alpha$ であることを意味しています。

このように、確率的チューリング機械は受理または拒否に関してが確率的な振る舞いとなるため、複数回の試行の結果として受理で終わる状態がどの程度観測されるかという観点で（多数決的に）受理の判断を行います。

量子チューリング機械

ここまで決定性チューリング機械とその拡張として確率的チューリング機械を見てきました。ここからは、確率的チューリング機械をさらに拡張した量子版である量子チューリング機械について見ていきます。
量子チューリング機械（Quantum Turing Machine: QTM）は多くの方（e.g. C. H. Bennett, P. Benioff, R. P. Feynman）により色々な機構が考案されていますが、中でもドイチュ（David Deutsch）のものが整っており特に有名です。
量子チューリング機械の状態遷移関数 $\delta$ は以下のように表現することができます。

$$\begin{align*} \delta(q_0, 0, q_0, 0, R) &= \alpha\tag{3}\\ \textcolor{red}{Q \times \Sigma \times Q \times \Sigma \times \Delta} &\textcolor{red}{\rightarrow} \textcolor{red}{\mathbb{C}} \end{align*}$$

• $Q$: 状態の有限集合
• $\Sigma$: テープ記号の有限集合
• $\Delta$: ヘッドの移動方向

式(3)は、先述の確率的チューリング機械の状態遷移関数である式(2)と似ていますが、右辺の取りうる値が実数ではなく複素数全体として定義されている点が異なります。式(3)は、$(q_0, 0, R)$ という状態遷移が起こる振幅が $\alpha$ であることを意味しています。この振幅の絶対値を2乗した値が、対応する状態遷移の確率となります。

ここで、確率的チューリング機械と量子チューリング機械の振る舞いがどのように異なるかを考えてみましょう。直感的なイメージを持ちやすくするため、それぞれ記憶容量が1bitであるような単純な確率的チューリング機械および量子チューリング機械で考えます。このとき、確率的チューリング機械および量子チューリング機械の構造はどちらも同一で図4のように表現することができます。

図4: 記憶容量が1bitの確率的チューリング機械および量子チューリング機械の構造

たとえば、この記憶容量が1bitの確率的チューリング機械の状態遷移が以下の場合、これは表と裏がそれぞれ確率 $\dfrac{1}{2}$ で出るようなコイン投げを行っている状況と同じように考えることができます。ここからはコイン投げを例として説明を行います。

$$\begin{align*} \delta(q_0, 0, q_0, 0, N) &= \dfrac{1}{2}\\ \delta(q_0, 0, q_1, 1, N) &= \dfrac{1}{2}\\ \delta(q_1, 1, q_0, 0, N) &= \dfrac{1}{2}\\ \delta(q_1, 1, q_1, 1, N) &= \dfrac{1}{2} \end{align*}$$

図5: コイン投げ（確率的チューリング機械）

今、裏という状態から開始して2回連続でコイン投げを行ったとします。この結果が裏となる確率を考えてみましょう。これは式(4)のように結果が裏となるような計算パスに関する確率を足し合わせることで得ることができます。

$$\left(\dfrac{1}{2} \times \dfrac{1}{2}\right) + \left(\dfrac{1}{2} \times \dfrac{1}{2}\right) = \dfrac{1}{2}\tag{4}$$

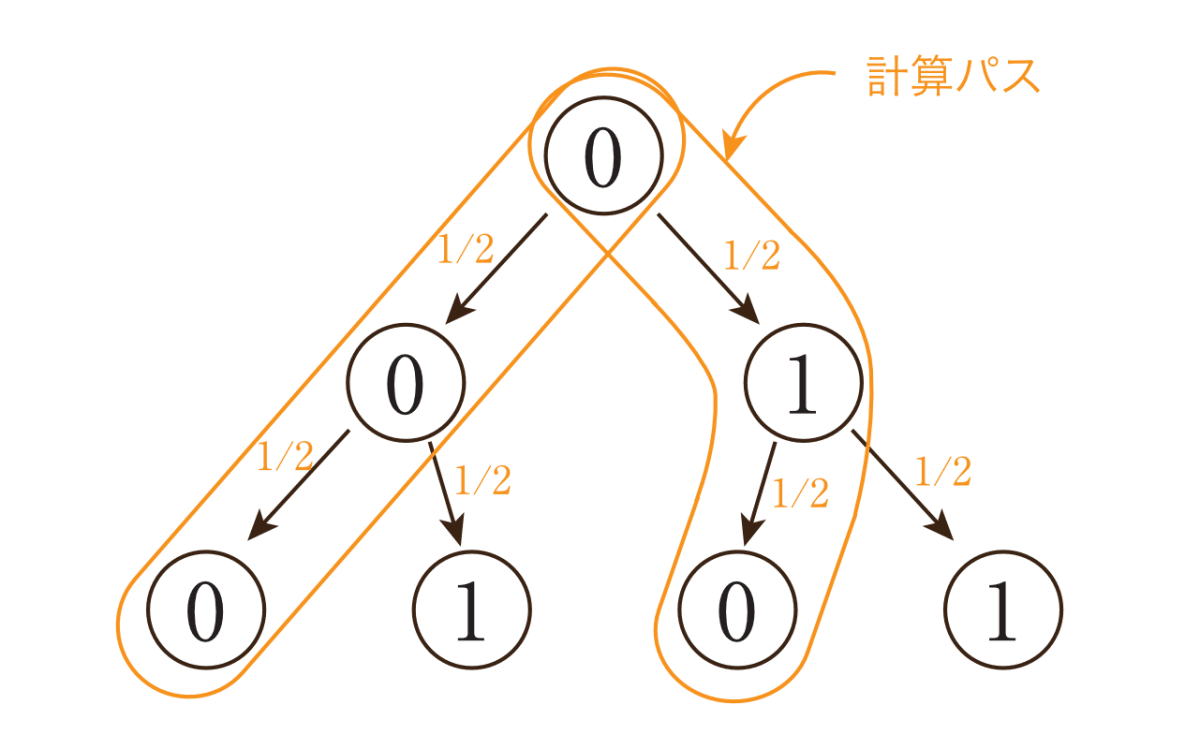
図6: コイン投げの計算パス（確率的チューリング機械）

次に、量子チューリング機械の場合でも考えてみましょう。以下に状態遷移関数の具体例^[3]および量子コイン投げの動作例を示します。

$$\begin{align*} \delta(q_0, 0, q_0, 0, N) &= \sqrt{\dfrac{1}{2}}\\ \delta(q_0, 0, q_1, 1, N) &= -\sqrt{\dfrac{1}{2}}\\ \delta(q_1, 1, q_0, 0, N) &= \sqrt{\dfrac{1}{2}}\\ \delta(q_1, 1, q_1, 1, N) &= \sqrt{\dfrac{1}{2}}\\ \end{align*}$$

図7: 量子コイン投げ（量子チューリング機械）

先ほどと同様に、裏から始めて2回連続でコインを投げた時に最終結果が裏になる確率を考えます。確率は振幅の絶対値の2乗で得られるため、以下の式(5)で計算することができます。

$$\left|\left(\sqrt{\dfrac{1}{2}} \times \sqrt{\dfrac{1}{2}}\right) + \left(-\sqrt{\dfrac{1}{2}} \times \sqrt{\dfrac{1}{2}}\right)\right|^2 = 0\tag{5}$$

ここで得られた結果は、確率が $0$ というものです。これは、振幅として負の値も足し合わされることにより生じており、確率的チューリング機械の場合には起こり得ない現象です。実は、量子チューリング機械では最終結果を観測するまでの途中経過であるコインが1回投げられてる時には、確率50%ずつで裏と表が同時に存在することになります。このように、コインの表と裏が同時に存在することを量子重ね合わせと呼びます。確率的チューリング機械では確率の和という正の干渉のみでしたが、量子チューリング機械では正の干渉と負の干渉も両方起こすことが可能なため、確率が $0$ となるような結果を生み出すことが可能です。

また、裏から始めて2回連続でコインを投げた時に最終結果が表になる確率を考えてみると、以下の式(6)のように $1$ となることが確認できます。

$$\left|\left(\sqrt{\dfrac{1}{2}} \times -\sqrt{\dfrac{1}{2}}\right) + \left(-\sqrt{\dfrac{1}{2}} \times \sqrt{\dfrac{1}{2}}\right)\right|^2 = 1\tag{6}$$

このように、量子チューリング機械では、量子重ね合わせと計算パスの正と負の干渉を利用することで、ある時点における複数の状態（たとえば、全ての計算パス）を同時に調べ、観測時点では計算結果に当たるような限定された状態に収束させることが可能となっています。 このような量子チューリング機械をモデルとするコンピュータのことを量子コンピュータと呼びます。

まとめ

本記事では、まず現代のコンピュータのモデルである決定性チューリング機械について確認し、状態遷移が決定的に定まらないとう点において決定性チューリング機械とは異なる構造を持つ非決定性チューリング機械、および乱数を用いたモデルとしての確率的チューリング機械についても確認を行いました。さらに量子版として拡張した量子チューリング機械を確率的チューリング機械と比較することで、量子力学的な重ね合わせの効果により複数の計算パスを同時並列的に調べることができるという振る舞いを確認しました。

チューリング機械は計算量理論という計算の複雑さに関する理論とも密接に関係しています。そしてこの計算量理論では、今回見てきた各種チューリング機械が現実的な時間でどのような問題まで解くことができるのかを議論することが可能となり、古典的コンピュータと比較した際の量子コンピュータの優位性を考える上でも重要な要素となってきます。今後はそのようなチューリング機械と計算量理論について、更には量子コンピュータの有効性に関する内容についてもまとめていきたいと思います。

参考

• 西野哲郎: 「情報科学セミナー 量子コンピュータ入門」，東京電機大学出版局，第１版，1998.
• 佐川弘幸，吉田宣章: 「量子情報理論」，丸善出版株式会社，第３版，2021.
• チューリングマシンの拡大と複雑性（2021年11月07日アクセス）
• [技術解説] 高速化の鍵は量子の「もつれ」や「重ね合わせ」ーー 量子コンピューターの原理を知る（2021年11月08日アクセス）

脚注

1. 本記事で紹介している構造以外にも、複数のテープを持つものなど異なる構造のチューリング機械も存在します。

2. ここでは二分木で記載していますが、任意の $n \ge 2$ に対しても同様に考えることができます。

3. 一般的には振幅は複素数の値を取りますが、本記事では実数を用いた例にしています。