Unity UnlitシェーダーでのPhong反射モデルの実装
Lightingの基本を学ぶため、光の影響を受けないUnlitシェーダーで、Phong反射モデルを実装した。
今回、Phong反射モデルを実装するにあたり、以下のように区分して順に考えた。
- 直接光
- 拡散反射
- 鏡面反射
- 間接光
- 環境光
特に光の計算を行わなかった場合は、以下のようなモデル表示となる。

直接光
Lambert拡散反射モデル
「物体の各点の法線ベクトルnとライトのベクトルLの内積の値t
を計算することで、各法線の始点でのライトの強度が計算できる」というモデル。
例として原点中心の半径1の球で考える。
ライトのベクトルLを
とすると、
最もライトの強度が強い点は、(1, 0, 0)になる。
球が原点中心であるから、
と求まる。
逆に、最も暗い点は、(-1, 0, 0)になる。
と求まる。
ただ内積の値が小さいほど、明るいだと扱いづらいので、求めた内積に-1をかけたもの(-t)を用いる。
Lambert拡散反射モデルの計算を反映した表示結果を以下に示す。
-tが1に近いほど白で表示され、0以下は黒となる。
これを見ると、Lambert拡散反射を反映するだけでもだいぶそれっぽい影がついていることがわかる。
また、光が当たっていない部分が完全に黒になっているが、のちに間接光やHalf Lambertを考えることで、完全な黒ではないようにする。

Lambert拡散反射モデルを反映した球
Half Lambert
Lambert拡散反射モデルでは、領域の半分が真っ黒で描画されてしまう。
以下の青いグラフは、拡散反射の強度tについて描画したものである。
このグラフのy座標が負の値をとるθの箇所で真っ黒な表示になる。
Half Lambertは、この負になる領域をなくし、全体として値を持ち上げたモデルである。
Half Lambertにおけるtをt_halfとすると、
と書ける(オレンジ色のグラフがt_half)。
以下に示した球の表示例でもわかるように、Half Lambertの方が、全体として明るい表示になる。
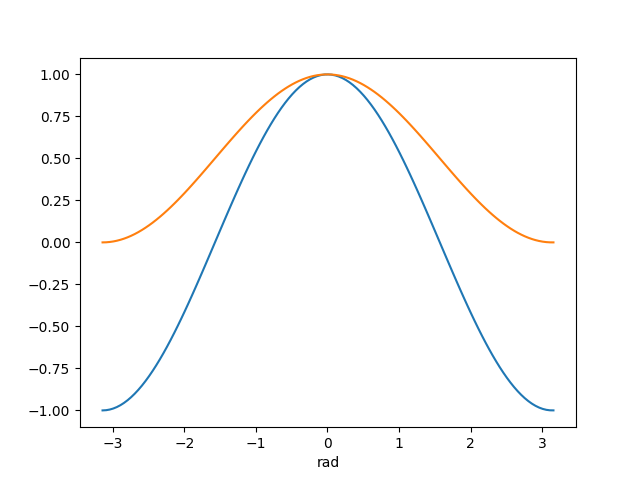
青いグラフ:y=cos(θ)、オレンジ色のグラフ:y=(1 + cos(θ) / 2)

Half Lambert適用前の球の表示(Lambert適用)
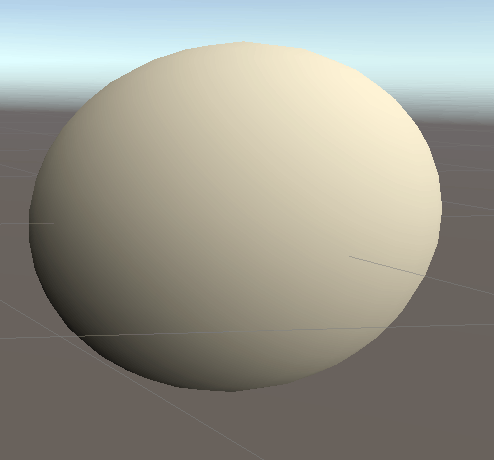
Half Lambert適用後の球の表示
Phong鏡面反射モデル
物体の表面の各点で反射した光のベクトルと、反射点からカメラへ向かうベクトルの向きが一致しているときに最も鏡面反射が強くなるという考え方に基づいたモデル。
ライトの単位ベクトルをL、反射点での法線ベクトルをN、求める反射ベクトルをRとすると、
反射ベクトルRは
と求まる。
これを計算するための関数がHLSLの組み込み関数(reflect関数)として用意されているので、今回はこれを用いた。
ここで得られた反射ベクトルRと、反射点からカメラへ向かうベクトルEの内積を鏡面反射の指標として用いる。
この指標をtをすると、
であり、tが負の場合については、Lambert拡散反射モデルのときと同様に、光の寄与がない(t=0)ものとして考える。
すると、tの範囲は、
このtを累乗することで、鏡面反射の絞りを実現する。
累乗の指数が大きいほど、最終的な値は小さくなる。
つまり、累乗が大きいほど、最も強く反射する点から離れたときの光の反射強度の減衰率が高くなり、絞りが強い鏡面反射になる。
この累乗値は、今回実装したShaderでは、_SpecularApertureという変数に対応する。

Phong鏡面反射モデルで計算した、球の鏡面反射の強度(累乗の指数2)
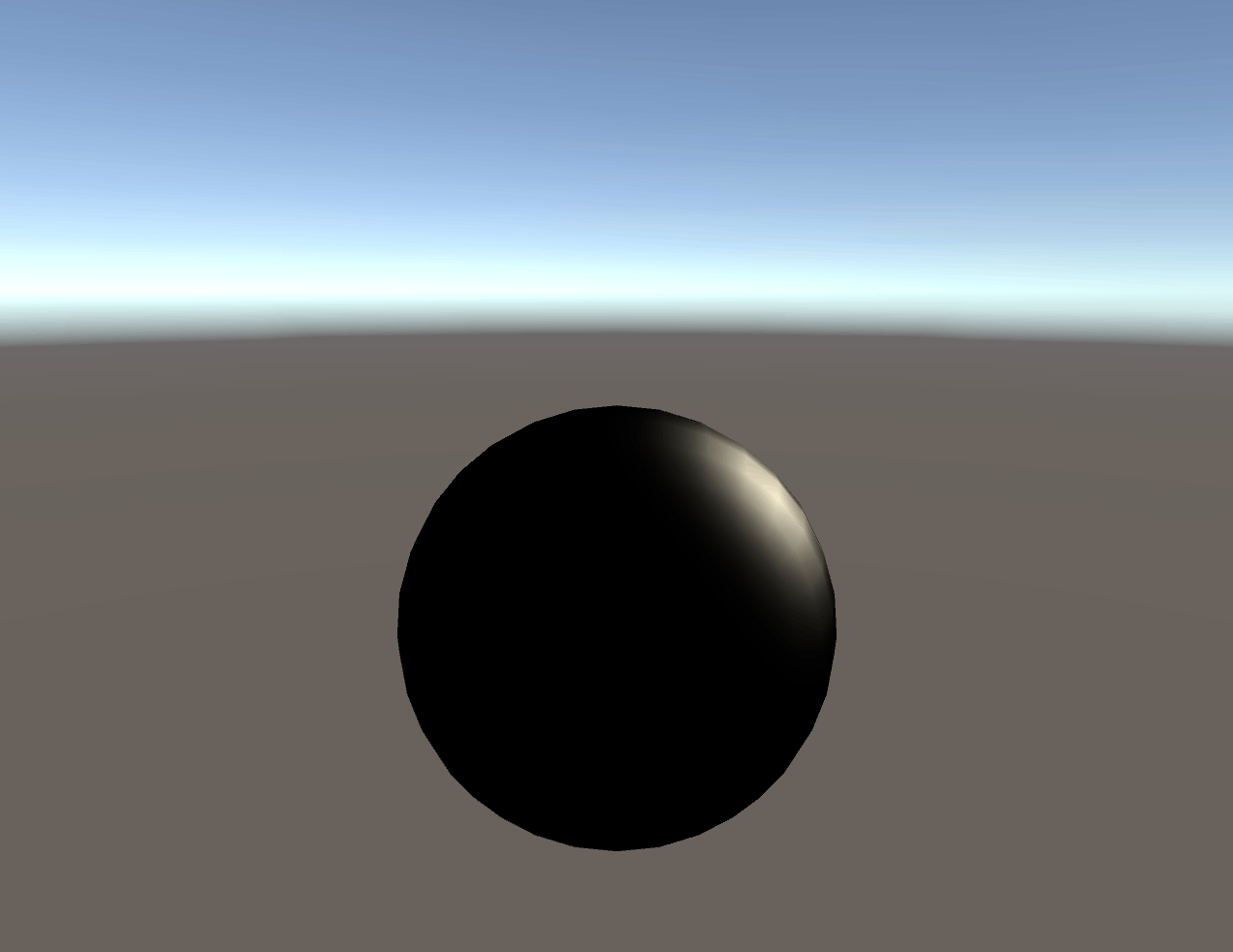
Phong鏡面反射モデルで計算した、球の鏡面反射の強度(累乗の指数5)

Lambert拡散反射とPhong鏡面反射の結果(累乗の指数5)を足し合わせたもの
間接光
正確な間接光を反映するには、直接光がどのように反射するかを計算しなければならないが、計算量が膨大になってしまう。
そのため、簡単なモデルとして昔から用いられてきた環境光(アンビエントライト)を今回は採用する。
環境光(アンビエントライト)
「物体は一律で同じ間接光を受けている」
という大胆な近似を行う計算モデルで、最終的な光の強度に一定の値を加えることで表現する(今回実装したShaderでは_EnvironmentLightWeight変数に対応)。
最後に、今回実装したシェーダーのソースコードを示す。
Shader "Unlit/LambertPhongEnvironment"
{
Properties
{
_MainTex ("Texture", 2D) = "white" {}
_SpecColor ("Specular Color", Color) = (1, 1, 1, 1)
_SpecularAperture ("Specular Aperture", float) = 5.0
_EnvironmentLightWeight ("Environment Light Weight", float) = 0.2
}
SubShader
{
Tags { "RenderType"="Opaque" }
Pass
{
Tags { "LightMode" = "ForwardBase" }
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
#include "Lighting.cginc"
struct appdata
{
float4 vertex : POSITION;
float3 normal : NORMAL;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
float3 normal : NORMAL;
float4 vertex : SV_POSITION;
};
sampler2D _MainTex;
float4 _MainTex_ST;
float _SpecularAperture;
float _EnvironmentLightWeight;
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.normal = UnityObjectToWorldNormal(v.normal);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
return o;
}
fixed4 frag (v2f i) : SV_Target
{
float3 lightDirection = normalize(_WorldSpaceLightPos0);
// Lambert拡散反射の強度を求める
float diffuseT = dot(i.normal, lightDirection);
// 0 ~ 1でClampする
//Half Lambertのときは、
//diffuseT = 0.5 + 0.5 * diffuseT;
diffuseT = saturate(diffuseT);
fixed3 lightColor = _LightColor0.xyz;
// 拡散反射光を求める
fixed3 diffuseLightColor = lightColor * diffuseT;
// ライトの反射後のベクトルを求める
fixed3 reflectionVector = reflect(lightDirection, i.normal);
// ライトの反射点からカメラの位置を結ぶベクトルの単位ベクトルを計算する
float3 toEyeVector = normalize(_WorldSpaceCameraPos - i.vertex.xyz);
// Phong鏡面反射モデルの強度を求める
float specularT = dot(reflectionVector, toEyeVector);
// 0 ~ 1でClampする
specularT = saturate(specularT);
// 鏡面反射の強さを絞る
specularT = pow(specularT, _SpecularAperture);
// 鏡面反射光を求める
fixed3 specularLightColor = lightColor * specularT * _SpecColor;;
// 拡散反射光と鏡面反射光を足し合わせたものを、最終的な直接光の寄与とする
fixed3 finalLightColor = diffuseLightColor + specularLightColor;
// 間接光として、環境光を一様に受けていると考え、環境光の影響を加える
finalLightColor.x += _EnvironmentLightWeight;
finalLightColor.y += _EnvironmentLightWeight;
finalLightColor.z += _EnvironmentLightWeight;
fixed4 col = tex2D(_MainTex, i.uv);
col.xyz *= finalLightColor;
return col;
}
ENDCG
}
}
}
Discussion