データサイエンス勉強会第 2 回
データサイエンス勉強会第 2 回
はじめに
アイディオットのデータサイエンティスト、佐藤です。
弊社では、全社的なデータサイエンスリテラシーの向上のため、データサイエンス勉強会を不定期開催しています。
今回は 2024 年 5 月 7 日(火)に行った第 2 回の内容をお送りいたします。
概要
勉強会の目的
- 普段の業務で データがどう役に立つのか を知る。
- データを主軸に置くアイディオットだからこそ、 データって何だろう? を深める場を作る。
レベル感
統計検定 2 級程度。
目標
数式をなるべく使わず、図を多く用いてデータサイエンスのイメージを掴む。
第 2 回の内容
今回は、データの種類・ばらつきについて見ていきます。

第 2 回の目的
- 4 種類のデータのイメージを持つ
- 標準偏差のイメージを持つ
データの種類
4 種類のデータ
ここでは、データの種類、特に 4 種類のデータについてイメージを持っていただきます。
まずは下の図を見てください。

一口にデータといっても、一段階抽象度を下げると「質的変数」と「量的変数」があります。
「質的変数」とは、計算することも数値で表すこともできない、定性的なデータ。例えば、羊羹の種類にも栗羊羹や煉羊羹があることをイメージしていただけるとわかりやすいかと思います。
一方、「量的変数」とは、計算でき、数値で表せる定量的なデータです。50g の羊羹が 2 個あれば、総重量は 100g と表せるようなものです。
「量的変数」の抽象度をさらに下げると、離散変数や連続変数といった変数が出てきますが、こちらは一旦忘れてください。
ともかく、今回お話しさせていただく 4 種類のデータとは、この「質的変数」と「量的変数」に属するデータになります。
「量的変数」には比尺度、間隔尺度、順序尺度の 3 つのデータがあります。
一方、「質的変数」には名義尺度が含まれます。
今回は、こちらの 4 つの「尺度」データについて見ていきます。
比尺度
比尺度とは、0 が存在し、四則演算ができることが特徴です。
例えば、以下の図のように、60kg の 2 倍は 120kg、40kg の 2 倍は 80kg など、増減値は違いますが、基準値が決まっていれば 1:2 で表せられますよね。
このように、比で数字を比べられるものを 比尺度といいます。

間隔尺度
間隔尺度とは、0 がなく、数字の感覚は等しいが、足し算・引き算しかできないデータを指します。
例えば、以下の図のように、西暦 1900 年の 100 年前は西暦 1800 年、100 年後は西暦 2000 年と言えます。
一方、西暦 100 年の半分は西暦 50 年とか、倍にすると西暦 200 年とかは言えないですよね。
このように、足し算・引き算しかできないものを 間隔尺度といいます。

順序尺度
順序尺度とは、変数間の順序に意味はあるが、四則演算できないものを指します。
例えば、以下の図のように、試合結果の順位は 1 位 > 2 位 > 3 位と言った順序はありますが、1 位と 2 位を足し合わせても何の意味もないですよね。
このように、変数間の順序に意味があるものを 順序尺度といいます。

名義尺度
順序尺度 のみ「質的変数」に属し、計算できないが数値で表すことができないデータを表現できます。
例えば以下の図のように、取扱商品データに煉羊羹、栗羊羹、抹茶羊羹…などといった種類があることをイメージしていただけるとわかりやすいかと思います。

標準偏差
代表値
次に、あるグループのデータのばらつきを表す、標準偏差について見ていきます。
その前に、簡単に、あるグループの特性を表す、代表値について見ていきましょう。
代表値は「平均値」・「中央値」・「最頻値」の 3 つがあります。
平均値
こちらは、よく耳にされることがあるかと思います。
平均値は最も広く知れ渡った代表値で、手軽にグループの特性を表すことができますが、外れ値の影響を受けやすいといった特性を持ちます(下図の右図がその例ですね)。

中央値
こちらは、データを順番に並べ、真ん中にくる値をとったものを指します。
下図は先ほどの平均値では外れ値の影響を受けてうまく表現できませんでしたが、中央値を示すと納得できるかと思います。

最頻値
読んで字の如く、最もよく出現する値をとったものを指します。
こちらも外れ値に強いといった特性を持ちますが、一方で偏りに引っ張られるといった特性を持ちます。
先ほどから、私たちが問題にしているデータでも、見事に偏りに引っ張られてしまっていますね。

代表値の問題
さて、ここで下図のデータについて考えて見ましょう。
データのばらつき具合は同じですが、どの代表値も同じ値を示していますね。
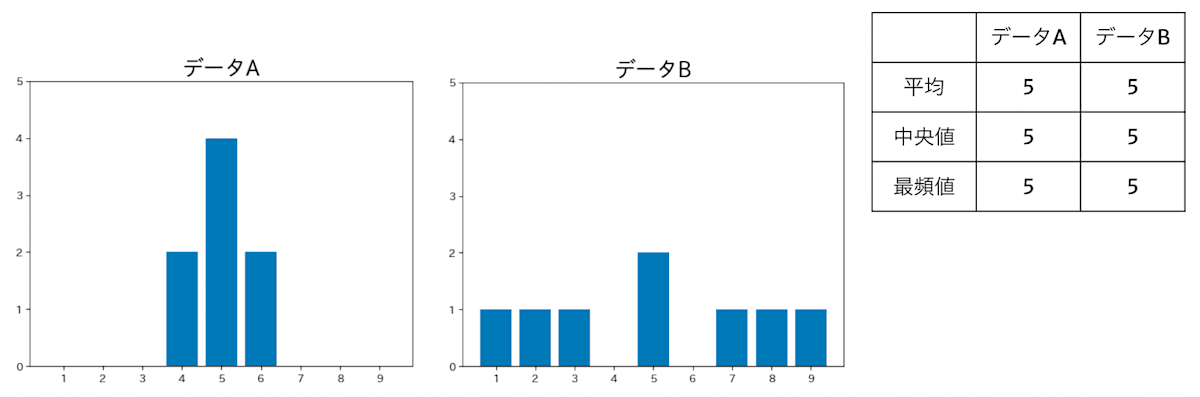
代表値はあるグループの特性を 1 つの値で言い表すことができる一方、データのばらつきを表現することができません。
そこで標準偏差が出てきます。
標準偏差とは
標準偏差とは、代表値を平均値としたとき、データが取りうる値の範囲を数値化したものです。
平均値に標準偏差を足し算引き算することで、そのデータが取りうる値の範囲を知ることができます。
標準偏差をそのまま足し算引き算することで、約 68% の確率でデータが収まる値を、標準偏差を 2 倍にしたものを使うと、さらに約 95% の確率でデータが収まる範囲を知ることができます。

まとめ
第 2 回は、以下 2 点を目標にして内容を見てきました。
これまでの内容を振り返り、答えを下に加えて改めて整理します。
- 4 種類のデータのイメージを持つ
→ データには、比尺度・間隔尺度・順序尺度・名義尺度 の 4 種類があり、計算できるかどうかで分けることができる。
粒度を荒くすると、「量的変数」と「質的変数」に分けられる。 - 標準偏差のイメージを持つ
→ 標準偏差とは、平均値を代表値とした データが取りうる値の範囲。
代表値だけでは表現できない、データのばらつき具合を知ることができる。
次回
次回は、相関と回帰についてお伝えし、簡単な予測についてもする予定です。
目標として、データのばらつきから相関と回帰についてイメージを持っていただくことです。
ここまでお読みいただき、ありがとうございました。
あとがき
AI・データ利活用をリードし、世界にインパクトを与えるプロダクトを開発しませんか?
アイディオットでは、今後の事業拡大及びプロダクト開発を担っていただけるエンジニアチームの強化を行っております。
さらに会社の成長を加速させるため、フロントエンドエンジニア、バックエンドエンジニア、インフラエンジニアのメンバーを募集しております!
日本を代表する企業様へ自社プロダクトを活用した、新規事業コンサルティング、開発にご興味のある方はお気軽にご連絡ください。
【リクルートページ】
https://aidiot.jp/recruit/
【募集ポジション一覧】
https://open.talentio.com/r/1/c/aidiot/homes/3925
【採用についてのお問合せ先】
株式会社アイディオット 採用担当:佐藤
メールアドレス:recruit@aidiot.jp

Discussion