🌲
生成規則からLR(0)構文解析表を1から作る記事

2025/05/15に公開
シンプルな生成規則を使って､LR(0)文法に基づいた構文解析表をあたたかみのある手作業で作成する記事です｡これは先日書いた記事
https://zenn.dev/ahoxa1rx/articles/88e6ff1014cba6
の続きでもあります｡ただ大した解説はしていないので↑の記事は読まなくても問題ありません｡

なお今回扱った内容の成果物は､LR_parserにあげてあります｡結果だけ知りたい方はそちらへどうぞ｡

 この記事は誰向けなのか60%くらい自分向けに書いています｡
パーサ､構文解析器を実装してみたいけど何をしたら良いのかがわからない人
パーサジェネレータを実装したいけれど自分が定義した文法からコードに変えるところで挫折した人
構文解析やオートマトンの知識がうっすらある人
......のような人たちに向けて40%ほどです｡私自身勉強途中なので､不備等あればコメントなどで指摘していただけると助かります｡[1]

また記事の末尾には参考資料を乗せておきますので､そちらを参照してみてください｡

 構文解析について(プログラミング言語文脈での話)!筆者はこの分野について学習途中であるため不正確な表現が含まれる場合があります｡
人間にとって読みやすいよりの文字列の並び､コードを現行のコンピュータが理解できるコードに変換するインターフェースとしてコンパイラやインタプリタがあります｡それらが行っている操作の一つが構文解析です｡

構文解析は､トークン列を読み取り､別で与えられている文法(形式文法)に則りコンピュータに理解しやすい形である構文木あるいは抽象構文木に変換することです｡

 構文解析と形式文法簡単な足し算･掛け算の計算を処理することを考えます｡
簡単な足し算･掛け算の例
1 + 2 * 3 + 4
もちろんこれは答えを｢11｣として処理できるわけですが､それはあくまで四則演算の約束事を遵守できる場合の話です｡

四則演算は演算子の処理を左から右に行うが､掛け算･割り算(*/÷)は足し算･引き算(+/-)より優先して計算するという約束で成立しています｡もし｢演算子の処理を左から右に行う｣のみの約束しか知らない場合､この計算は｢13｣という結果になるでしょう｡あるいは､｢右から左へ行う｣約束のみの場合なら､｢15｣という結果になります｡
一つの文字列､あるいは計算式をとっても約束事が変わると大きく結果が変わることになってしまいます｡そうした文字列だけでは決定できない構造を一つに定める約束事として､生成規則が存在します｡

文字列あるいはトークン列に木構造を与えるための文法です｡[2]
生成規則の表し方にはBNF記法などがありますが､今回は簡単に左辺->右辺の形で表すことにします｡
生成規則の例
E -> E + T

 構文解析と生成規則とオートマトン構文解析ではこの生成規則(あるいは形式文法)を用いながら与えられたトークン列を構文木に変換します｡

生成規則は理論の表現において優れていますが､実際にコンピュータで構文解析を行う場合不十分です｡そこでよくオートマトンが用いられます｡

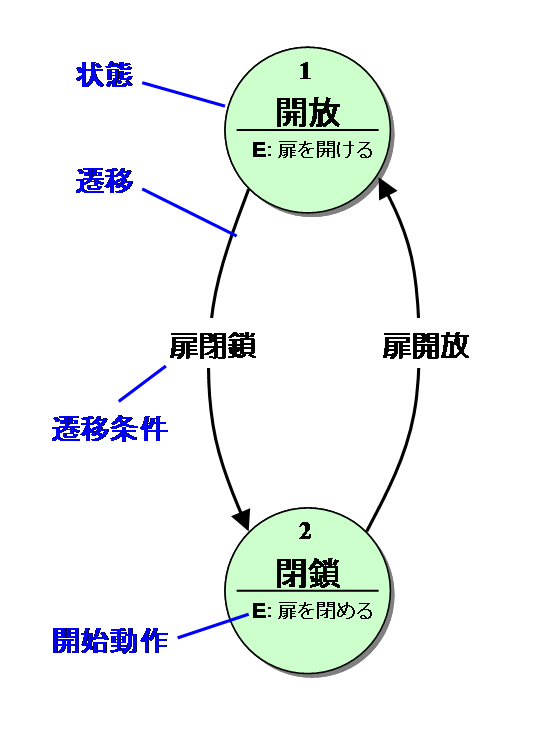
オートマトンは入力によって状態を切り替えるモデルで､丸と矢印の集合でよく表されます｡


Wikipedia/有限オートマトンより
オートマトンにはいくつか種類があり､構造や性質によって分類されています｡

構文解析において使用するオートマトンはおおよそ以下の4つで､下のものほど表現･分析できる文法の幅が大きいです｡構文解析するだけであればこれらの違いについては｢ふーんそうなんだ｣で流しても大丈夫だと思います(もちろん知っておくに越したことはありません)｡
有限オートマトン: 状態と遷移のみ｡
プッシュダウンオートマトン: 状態と遷移に加えて､スタック(先頭に挿入して先頭から取り出す制約のある記憶装置)を持ちます｡a^nb^nのような｢連続したaのあとにbも同じ個数だけ連続して存在する文字列｣などを解析可能です｡
線形拘束オートマトン: 読み書きできる有限長のテープと状態､遷移を持ちます｡
チューリングマシン: 線形拘束オートマトンが無限長のテープを持っているものです｡
厳密な定義などはここでは解説しないので､適宜調べて補完してください｡

オートマトンは上の画像のように状態を入力を表した矢印を持つ図で表現されますが､プログラミングや数学の関数としておおざっぱに表現すると
f(現在の状態, 入力記号) = (次に遷移すべき状態/スタックやテープへの操作)
の集合として表現できます｡引数が2つなので､先ほどの図を表に起こすと､


↓現在の状態/入力記号→
扉閉鎖
扉開放


開放
扉開放


閉鎖

扉閉鎖

このような表現ができます｡パーサジェネレータの実装上2次元配列で表現できるというのも便利です｡

 構文解析の手法プログラミング言語を設計するとき､もちろん人間にわかりやすい様な規則を用いたいわけですが､リッチな､機能がたくさんある言語に対応する文法を書くとその分複雑な実装になっていきます｡

実装の難易度と解析できる文法の多様性のトレードオフになるため､様々な解析手法がこれまで提案されてきました｡
LL(k): シンプルな再帰で解析する手法｡始まりの生成規則からトークン列に合致する生成規則を適用していく手法です｡左から右へ(Left-to-right)読んでいき､最左導出(Leftmost-derivation)[3]を行う方法です｡kは先読み文字の個数で､現在解析中の文字からk個先読みするすることです｡トップダウン構文解析の一つです｡実装が簡単な分､直感的な生成規則だとLL(k)で解析できない場合が多く[4]､生成規則を更に一段階加工する必要があります｡
LR(k): トークン列を読み込んで合致する生成規則を下にトークン列を還元していく手法｡左から右へ(Left-toright)読んでいき､最右導出(Rightmost-derivation)[5]を逆順[6]で行います｡こちらの方法は実装が複雑になりやすい分､解析できる文法が広いです｡こちらはさらに構文解析表の構築方法に派生があり､それぞれにメリット･デメリットが存在します｡
LR(0): 先読みしない方法です｡
LR(1): 受容できる文法が多い代わりに構文解析表が大きくなりやすいです｡また構文解析表が疎になりやすいです｡
LALR(1): LR(1)より受容できる文法が少ないですが､LR(1)のデメリットである構文解析表の大きさを抑えることができます｡yaccなどの代表的なパーサジェネレータはLALR(1)を採用しています。
SLR(1): LR(1)･LALR(1)より受容できる文法が少ないです｡LALR(1)より構築が簡単です｡
GLR(1): 取りうる状態をすべて試行するLR法です｡自然言語向きな解析手法です｡
LR(k) (k > 1): 先読み文字が多いので受容できる文法が多いですが､状態数が多いため実用向きではありません｡

......いっぱいあります!他にもありますがキリがないのでこのあたりで打ち切らせてください｡

 本題: LR(0)構文解析表を作ってみよう! ~準備編~前置きが長くなりすぎたな~と思いつつ､早速(?)構文解析表を作っていきましょう｡

 今回扱う文法終端記号(生成規則の左辺に現れない記号､これ以上生成規則で置換されないトークン)

< > $

$ は構文解析の終了記号

非終端記号(生成規則の左辺に現れる記号､実際のトークン列には現れない構文解析中に便利な記号)
E

生成規則
E -> <>
E -> <E>
E -> EE

開始記号
E

入れ子ありのカッコで､開くと閉じるが対応するといった感じです｡

本来形式文法をきちんと表す場合は､\delta()に当たる状態遷移をすべて書く必要がありますが､ここで書くと煩雑なので一旦省略します｡

 LR法で出てくる操作の説明LR法はプッシュダウンオートマトンをベースにした構文解析表を必要としますが､その際にスタックへの操作や状態の変更､構文木の出力に必要な操作を紹介します｡

Shift(i)命令: 状態をiに遷移させて､スタックにiをプッシュします｡

Reduce(n)命令: 生成規則のn番目を適用して入力記号にその生成規則の左辺の非終端記号を設定します｡またスタックから適用した生成規則の右辺のトークンの個数分ポップします｡

Goto(i)命令: 非終端記号が入力にある場合の命令です｡対応する状態に遷移し､その状態をスタックにプッシュします｡

Accept命令: 構文解析が正しい状態で終了します｡

 LR(0)構文解析表を作ってみよう! ~ほんへ~この通りにやるとLR(0)で構文解析するための構文解析表が完成します!頑張っていきましょう!

 文法を強化する生成規則に特別な開始記号S'を左辺[7]､開始記号Eを右辺に持つ生成規則を形式文法の生成規則に追加します｡

現在の生成規則は以下のようになります｡
S' -> E
E -> <>
E -> <E>
E -> EE

 どこまで読んだかを示す記号の導入.という記号を生成規則の右辺に導入します｡

.より左にあるトークンはすでに読まれたことを表します｡
S' -> .E
E -> .<>
E -> .<E>
E -> .EE

 S'を含む生成規則をアイテム集合I0に追加するアイテム集合を導入します｡.記号ありの生成規則をアイテム(項)としてその集合をアイテム集合と呼びます｡このアイテム集合を､これから行う手順で構築すると機械的に構文解析表の素ができます｡
アイテム集合I0
S' -> .E

 繰り返し手順➀.に続く記号が非終端記号の場合､アイテム集合に対応する生成規則を追加するI0に含まれているアイテムの.に続くトークンには非終端記号のEが含まれています｡

よって､Eを左辺に含む生成規則を追加します｡

この場合追加されたE -> .EEはさらに.のあとにEを含みますが､すでにEを含む生成規則を追加済なのでこれ以上は必要ありません｡
アイテム集合I0
S' -> .E
E  -> .<>
E  -> .<E>
E  -> .EE

 繰り返し手順➁.に続く終端記号･非終端記号それぞれについて新規のアイテム集合を定義し､.を右に一つずらす!ここからお絵かきになるので筆記用具を手元において実際にやってみてください
I0のアイテム集合の.に続く終端記号･非終端記号それぞれに対応するアイテムを用いてアイテム集合を作成します｡その際､.を一つ右にずらします｡

アイテム集合は状態､アイテム集合生成自体に使った記号が遷移する際の入力記号になります｡
I0-----------        I1----------
|S' -> .E   |   <   | E -> <.>  |
|E  -> .<>  |  -->  | E -> <.E> |
|E  -> .<E> |       -------------
|E  -> .EE  |
-------------
     |E
     v
I2------------
|  S' -> E.  |
|  E  -> E.E |
-------------
この2つの手順を､I0アイテム集合に含まれるすべての生成規則で.が一番右にある(例えば今の状態のI2にあるS' -> E.)アイテムがどこかのアイテム集合に所属するまで繰り返します｡
左辺に.Eが存在するので生成規則を追加
I0-----------        I1----------
|S' -> .E   |   <   | E -> <.>  |
|E  -> .<>  |  -->  | E -> <.E> |
|E  -> .<E> |       | E -> .<>  |
|E  -> .EE  |       | E -> .<E> |
-------------       | E -> .EE  |
     |E             -------------
     v
I2-----------
| S' -> E.  |
| E  -> E.E |
| E -> .<>  |
| E -> .<E> |
| E -> .EE  |
-------------
次の図がI1とI2について.に続く記号に基づいて新規のアイテム集合と遷移を書いた図になります｡
.に続く記号それぞれでアイテム集合を作成+非終端記号から生成規則を追加
                          <
                        -----
                        v   |
I0-----------       I1----------      
| S' -> .E  |   <   | E -> <.>  |  >  I3-----------
| E  -> .<> |  -->  | E -> <.E> | --> |  E -> <>. |
| E  -> .<E>|       | E -> .<>  |     -------------
| E  -> .EE |       | E -> .<E> |
-------------       | E -> .EE  |
     | E         ↗  -------------
     v          | <       | E
I2-----------   |         v
| S' -> E.  |---｣    I4-----------
| E  -> E.E |       | E -> E.E  |
| E -> .<>  |       | E -> <E.> |
| E -> .<E> |       | E -> .<>  |
| E -> .EE  |       | E -> .<E> |
-------------       | E -> .EE  |
     | E            -------------
     v
I5-----------
| E -> EE.  |     
| E -> E.E  |
| E -> .<>  |
| E -> .<E> |
| E -> .EE  |
-------------
アイテム集合を新規に作る場合は､すでに同じアイテム集合がある場合はそちらにつなげてください｡今回の場合､I1の<の場合はE -> <.>とE -> <.E>になり､.のあとにEが続くので生成規則を追加するとI1になるので<の矢印がそのままI1に向きます｡

と､長文でまくしたてられても(私は)わからないので､少し噛み砕いておくと､
I1から'<'で遷移する場合のアイテム
I1-----------      Ix-----------
| E -> <.>  |  <   | E -> <.>  |
| E -> <.E> | ---> | E -> <.E> |
| E -> .<>  |      -------------
| E -> .<E> |
| E -> .EE  |
-------------
便宜上作成できるアイテム集合をIxとします｡Ixのアイテムのうち､E -> <.E>という.のあとに非終端記号が含まれるアイテムがあるため､Eを左辺に持つ生成規則をIxに追加します｡
Ixに'E'を左辺に持つ生成規則を追加
I1-----------      Ix-----------
| E -> <.>  |  <   | E -> <.>  |
| E -> <.E> | ---> | E -> <.E> |
| E -> .<>  |      | E -> .<>  |
| E -> .<E> |      | E -> .<E> |
| E -> .EE  |      | E -> .EE  |
-------------      -------------
I1とIxを比較すると同じアイテム集合であるというのがわかると思います｡

等価なアイテム集合が存在する場合､遷移をどちらに向けるべきかを(自動的に生成したい場合)機械は判定できないですし､人間も迷う原因になるので､等価なアイテム集合ができた場合はアイテム集合を増やさず遷移の向きをすでに存在するアイテム集合に向けるようにしましょう｡
以下の2点を満たせば構文解析器のオートマトンが完成します｡
すべて生成規則の末尾に.がついたアイテムがどこかに一つずつ存在すること
状態遷移がすべて書き切られていること
完成したアイテム集合と遷移はこのようになります｡アイテム集合付きではありますが､状態と遷移が書かれているためこの図のことを状態遷移図と呼びます｡
完成した状態遷移図
                          <
                        -----
                        v   |
I0-----------       I1----------      
| S' -> .E  |   <   | E -> <.>  |  >  I3-----------
| E  -> .<> |  -->  | E -> <.E> | --> |  E -> <>. |
| E  -> .<E>|       | E -> .<>  |     -------------
| E  -> .EE |       | E -> .<E> |
-------------       | E -> .EE  |
     | E         ↗  -------------
     v          | <     ^ | E
I2-----------   |     < | v
| S' -> E.  |---｣    I4----------  >   I6-----------
| E  -> E.E |   |   | E -> E.E  | ---> | E -> <E>. |
| E -> .<>  |   |   | E -> <E.> |      -------------
| E -> .<E> |   |   | E -> .<>  |
| E -> .EE  |   |   | E -> .<E> |
-------------   |   | E -> .EE  |
     | E        |   -------------
     v          |         |
I5-----------   |<        |
| E -> EE.  |   |         | E
| E -> E.E  |---｣         |
| E -> .<>  | <-----------｣
| E -> .<E> |
| E -> .EE  |
-------------
    ^   |
    -----
      E
作成しきったらアイテム集合の内容には興味がなくなるので､\delta(input, S_{now}) = S_{next}で表すと､
\delta(<, I_0) = I_1

\delta(E, I_0) = I_2
\delta(<, I_1) = I_1

\delta(>, I_1) = I_3

\delta(E, I_1) = I_4
\delta(<, I_2) = I_1

\delta(E, I_2) = I_5
\delta(<, I_4) = I_1

\delta(E, I_4) = I_5

\delta(>, I_4) = I_6
\delta(<, I_5) = I_1

\delta(E, I_5) = I_5
さて､ここまできたらあと少しです!この遷移を表に書き起こします!

 状態遷移図を表に書き起こす

アイテム集合↓/入力記号→
<
>
E


I0
I1

I2

I1
I1
I3
I4

I2
I1

I5

I3




I4
I1
I5
I6

I5
I1

I5

I6





 終了記号$の列を追加して､Accept命令を設定最初の設定を振り返りましょう｡

文法がこちらです｡
終端記号(生成規則の左辺に現れない記号､これ以上生成規則で置換されないトークン)

< > $

$ は構文解析の終了記号

非終端記号(生成規則の左辺に現れる記号､実際のトークン列には現れない構文解析中に便利な記号)
E

生成規則
E -> <>
E -> <E>
E -> EE

開始記号

E

そして構文解析の命令がこちらでした｡


Shift(i)命令: 状態をiに遷移させて､スタックにiをプッシュします｡

Reduce(n)命令: 生成規則のn番目を適用して入力記号にその生成規則の左辺の非終端記号を設定します｡またスタックから適用した生成規則の右辺のトークンの個数分ポップします｡

Goto(i)命令: 非終端記号が入力にある場合の命令です｡対応する状態に遷移し､その状態をスタックにプッシュします｡

Accept命令: 構文解析が正しい状態で終了します｡
今回は機械に分かりやすく文字列の終了を示したいので､$という終端記号を導入していましたね｡完成した状態遷移図を構文解析表にする際に､$を列に追加します｡

$は終了を表すため､正常な構文解析が出来た合図になります｡ここで追加された文法S' -> Eの出番です｡
オートマトンの状態がS' -> Eを含むアイテム集合I2の場合､$が入力に来れば正常終了､Accept命令に設定します｡
状態遷移図､もとい構文解析表は現在このようになります


アイテム集合↓/入力記号→
<
>
$
E


I0
I1


I2

I1
I1
I3

I4

I2
I1

Acc
I5

I3





I4
I1
I5

I6

I5
I1


I5

I6






 終端記号の列にある遷移をShift命令､非終端記号の列にある遷移をGoto命令に書き換えるShift(In)をSn、Goto(In)をGnとします。これは筆者の実装しているパーサジェネレータの仕様なので、各々実装したい場合は任意の表現に置き換えてください。


アイテム集合↓/入力記号→
<
>
$
E


I0
S1


G2

I1
S1
S3

G4

I2
S1

Acc
G5

I3





I4
S1
S5

G6

I5
S1


G5

I6






 Reduce命令の設定生成規則の末尾に.がついたアイテムのあるアイテム集合、今回の場合は、

E -> <>.


E -> <E>.


E -> EE.

これらが存在する、I3, I6, I5の行に対応する生成規則のReduce命令を書き込みます。

この際、非終端記号の列には書き込みません。これは構文解析表が厳密にはAction表とGoto表からなっており、還元動作はAction表に属する操作だからです。


アイテム集合↓/入力記号→
<
>
$
E


I0
S1


G2

I1
S1
S3

G4

I2
S1

Acc
G5

I3
R1
R1
R1


I4
S1
S5

G6

I5
S1
R3
R3
G5

I6
R2
R2
R2


(おや？と思った方や、構文解析に詳しい人ならば不審点があると思いますが、のちの章で解説します！)

 完成、そして動作検証ここまで手作業でお付き合いいただいた方はお疲れ様でした！

今回作成した構文解析表は筆者が実装したパーサジェネレータで動作を確認済みです。
https://github.com/raiga0310/LR_parser/blob/59620cb5717ca58753ba3f308f7092d3fae15b71/paren_reducer
https://github.com/raiga0310/LR_parser/blob/59620cb5717ca58753ba3f308f7092d3fae15b71/paren.csv
動作例
case: <><<>><>$
head: < || state: 0 || actionShift(1)  || stack : [0]
head: > || state: 1 || actionShift(3)  || stack : [0, 1]
head: < || state: 3 || actionReduce(1) || stack : [0, 1, 3]
head: < || state: 2 || actionShift(1)  || stack : [0, 2]
head: < || state: 1 || actionShift(1)  || stack : [0, 2, 1]
head: > || state: 1 || actionShift(3)  || stack : [0, 2, 1, 1]
head: > || state: 3 || actionReduce(1) || stack : [0, 2, 1, 1, 3]
head: > || state: 4 || actionShift(6)  || stack : [0, 2, 1, 4]
head: < || state: 6 || actionReduce(2) || stack : [0, 2, 1, 4, 6]
head: < || state: 5 || actionShift(1)  || stack : [0, 2, 5]
head: > || state: 1 || actionShift(3)  || stack : [0, 2, 5, 1]
head: $ || state: 3 || actionReduce(1) || stack : [0, 2, 5, 1, 3]
head: $ || state: 5 || actionReduce(3) || stack : [0, 2, 5, 5]
head: $ || state: 5 || actionReduce(3) || stack : [0, 2, 5]
head: $ || state: 2 || actionAccept    || stack : [0, 2]
[src/main.rs:154:5] parser.parse(String::from("<><<>><>$")) = [
    1,
    1,
    2,
    1,
    3,
    3,
]
テストもあります。網羅性はさておき

https://github.com/raiga0310/LR_parser/blob/59620cb5717ca58753ba3f308f7092d3fae15b71/src/main.rs#L187-L196
自分でパーサジェネレータを実装して確かめるのもおおいに有りだと思います！この記事で必要なことは解説しているはずなのでぜひチャレンジしてみてください！

 演習問題？この記事では<>の対応が取れる文法の構文解析表の作成をやってきました。

これ以外にもやってみたい方は、例えば以下のような文法で作成してみるといいでしょう。
E -> E + B
E -> E * B
E -> B
B -> 0
B -> 1
こちらは答えがLR法#LR(0)構文解析表の作成で作り方とともに紹介されています。作り終わった後に答え合わせをしてみてください。

 命令の衝突(Conflict)について実のところ今回扱った文法はLR(0)で解釈できる文法ではありません。

先程の構文解析表で、Reduce命令の設定を行ったときに、I5の列にShift命令がすでに存在しているところにはReduce命令を書かずにスルーさせました。

あらためてI5に含まれるアイテム集合を見ると、
I5のアイテムを抜粋
E -> EE.
E -> E.E
E -> .<>
E -> .<E>
E -> .EE
このうち、

E -> EE. Reduce命令に対応

E -> .<>/E -> .<E> Shift命令に対応

この2つのアイテムは入力が<の場合、ReduceするかShiftするかで2通りの解釈が存在し、単純にどちらを選択すればよいのかの衝突が発生します。
こうした衝突が発生する文法・生成規則は厳密にはLR(0)では解釈できない文法です。

とはいえ、嘘をついたわけではなく、構文解析表の構築においてどちらを優先するか決めておけば実のところ今回の衝突は問題になりません。今回はShift命令を優先させました。
衝突にも2種類存在し、
Shift-Reduce衝突
Reduce-Reduce衝突
で、今回の衝突はShift-Reduce衝突です。こちらはどちらの動作を優先するか決めておけばLR(0)として解釈できる文法です。

しかし、Reduce-Reduce衝突はLR(0)では単純に解決できません。こちらの解消は文法規則を変えるか、あるいは単純LR法を導入するかなどの対策があります。

 Shift優先なのか、Reduce優先なのかとはいえ、優先度をどうやって決めればよいのか、という疑問が浮かぶと思います。

今回の場合は単純なカッコの対応を出すだけなので、極論どちらでもよいのですが、実用的なプログラミング言語ではそうは行きません。

例えば、生成規則が
		 S -> if E then S
		 S -> if E then S else S
で、

if Cond then if Cond then A else Bのような文を構文解析する場合、elseブロックはどちらのifにつけるべきか、などが考えられます。まぁこの場合一般的には一番近いifと対応付ける文法が多いので、「どちらを優先させると人間にとって認知負荷が低いか」というところに焦点をあてて優先度を考えるとよいと思います。

 参考文献https://www.slideshare.net/slideshow/lr-parsing/57972777
https://ja.wikipedia.org/wiki/LR法
https://scrapbox.io/mrsekut-p/shift%2Freduceとreduce%2Freduceのconflict
http://tatamo.81.la/blog/2016/12/22/lr-parser-generator-implementation/

脚注
つまりある程度言語処理系に触れたことがある人向けです｡筆者がそのくらいの理解度なので ↩︎
文法･形式文法というと言語に用いる記号なども含めたものが正確です｡ ↩︎
解析中に生成規則による構文木への生成を行う際に､最も左に近い候補から生成規則を適用すること ↩︎
E -> E + Tのような左辺と右辺の先頭が同じ非終端記号の左再帰性のある生成規則の場合､最左導出なのでE + E + E + ...のように無限に適用が発生してしまいます｡プログラミング言語はこうした左再帰が結構出てきやすい(要検証)です｡ ↩︎
最左導出とは対象に､合致する生成規則が複数ある場合に右から適用していくこと ↩︎
ややこしい表現ですが､これはLR法がボトムアップ構文解析とよばれる､トークン列から生成規則を逆に用いて､生成規則の右辺に対応する箇所を左辺に変換､還元することで最終的に文法の開始記号を導くため逆順という表現を用いています｡ ↩︎
本来開始記号はSで表現されるのでならってS'にしておきます｡ ↩︎
生成規則からLR(0)構文解析表を1から作る記事

この記事は誰向けなのか

構文解析について(プログラミング言語文脈での話)

構文解析と形式文法

構文解析と生成規則とオートマトン

構文解析の手法

本題: LR(0)構文解析表を作ってみよう! ~準備編~

今回扱う文法

LR法で出てくる操作の説明

LR(0)構文解析表を作ってみよう! ~ほんへ~

文法を強化する

どこまで読んだかを示す記号の導入

`S'`を含む生成規則をアイテム集合`I0`に追加する

繰り返し手順➀`.`に続く記号が非終端記号の場合､アイテム集合に対応する生成規則を追加する

繰り返し手順➁`.`に続く終端記号･非終端記号それぞれについて新規のアイテム集合を定義し､`.`を右に一つずらす

状態遷移図を表に書き起こす

終了記号$の列を追加して､`Accept`命令を設定

終端記号の列にある遷移を`Shift`命令､非終端記号の列にある遷移を`Goto`命令に書き換える

`Reduce`命令の設定

完成、そして動作検証

演習問題？

命令の衝突(Conflict)について

Shift優先なのか、Reduce優先なのか

参考文献

Discussion
